El documento introduce conceptos básicos de robótica. Explica que la robótica industrial ha experimentado un crecimiento más lento de lo esperado debido a la complejidad de cálculos dinámicos. Sin embargo, herramientas de simulación como Matlab han permitido análisis y diseño más sencillos. Luego, describe elementos clave de robots como su estructura mecánica, grados de libertad, tipos de actuadores, sistemas de representación y más. El objetivo es presentar herramientas de modelado y simulación de robots usando comput

![Prácticas de Robótica utilizando Matlab®
Práctica 1 .- Pág. 1
Práctica 1
Introducción
La aparición de la robótica en la industria ha supuesto en los últimos 40 años una
importante revolución industrial, que sin embargo no ha tenido el crecimiento
exponencial que los pioneros de la robótica habían supuesto. Una de las razones para
este no tan rápido crecimiento ha sido la complejidad de los cálculos dinámicos de los
mecanismos robotizados. Las elegantes formulaciones matemáticas realizadas por los
padres de la dinámica requieren un gran número de cálculos que obligaba a realizar un
gran número de simplificaciones. Históricamente, el análisis, simulación y diseño de
robots ha supuesto una gran inversión de tiempo y capital, reservado para centros de
investigación y grandes fabricantes.
Sin embargo, la revolución del PC, está permitiendo la implantación de
herramientas sencillas de análisis y simulación de robots. Los programas de propósito
general para el modelado y la simulación de los sistemas mecánicos de múltiples
cuerpos han llamado poderosamente la atención durante esta ultima década. Un
programa CAD para la dinámica de los sistemas multicuerpos minimiza la posibilidad
del error humano en el manejo de modelos complejos, pero en la mayoría de ocasiones,
paquetes de software como IMP [Sheth-1972 ], ADAMS [Orlandea-1977], DISCOS
[Bodley-1978], DADS [ Nikravesh-1985], MEDYNA [Jaschinsky-1986] ofrecen unas
prestaciones mayores de las requeridas por el usuario. Además, utilizando paquetes de
análisis matemático general como MatLab se pueden implementar los algoritmos
clásicos de la dinámica computacional, y obtener una serie de herramientas que
permitan al usuario del PC realizar un diseño y análisis de su propio mecanismo.
En este sentido, este libro quiere presentar una serie de herramientas sencillas de
modelado computacional y simulación de robots, enfocadas a ser utilizadas en el diseño
paramétrico de robots y mecanismos tanto planares como espaciales en computadoras
personales. En contraste con los libros clásicos de robótica, en los cuales la teoría ocupa
un espacio predominante y es posible encontrar toda las bases de las herramientas que
aquí se utilizan, este libro pretende tener un enfoque eminentemente práctico, aportando
varias referencias para aquellos lectores que quieran ampliar las bases teóricas.](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-2-320.jpg)


![Prácticas de Robótica utilizando Matlab®
Práctica 1 .- Pág. 4
Mientras que los robots de servicio se definen como:
Dispositivos electromecánicos, móviles o estacionarios, dotados normalmente de
uno o varios brazos mecánicos independientes, controlados por un programa de
ordenador y que realizas tareas no industriales de servicio [Nostrand 90]
Para el estudio de la morfología de un robot se debe tener en cuenta que un robot
está formado por los siguientes elementos; estructura mecánica, transmisiones,
actuadores, sistema sensorial, sistema de control y elementos terminales.
Figura 1.3.- Elementos constitutivos de un robot industrial clásico
Estructura mecánica
Un robot está formado por una serie de elementos o eslabones unidos mediante
articulaciones que permiten un movimiento relativo entre cada dos eslabones
consecutivos. La constitución física de la mayor parte de los robots industriales está
inspirada en la anatomía del brazo y la mano humana.
Se definen como grados de libertad como los posibles movimientos básicos
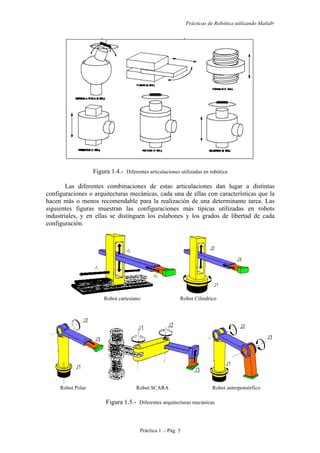
(giros y desplazamientos) independientes. La figura 1.4 muestra diferentes tipos de
articulaciones y los grados de libertad que aportan cada una de ellas.](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-5-320.jpg)

![Prácticas de Robótica utilizando Matlab®
Práctica 1 .- Pág. 7
Transmisiones y reductores
Las transmisiones son los elementos encargados de transmitir el movimiento
desde los actuadores hasta las articulaciones. Los reductores se incluyen con las
transmisiones y son los encargados de adaptar el par y la velocidad de la salida del
actuador a los valores adecuados para el movimiento de los elementos del robot.
Normalmente los actuadores se intentan situar lo más cerca de la base del robot,
con el fin de reducir al máximo el peso estático y la inercia de los eslabones finales, que
deben moverse con aceleraciones altas. Para ello es necesario utilizar sistemas de
transmisión que trasladen el movimiento hasta las articulaciones. La siguiente tabla,
extraída de [1] resume los sistemas de transmisión para robots. El lector que quiera
profundizar en el tema puede utilizar las referencias [1],[2] y [3] para obtener más
información.
Entrada-Salida Denominación Ventajas Inconvenientes
Circular-Circular Engranaje
Correa dentada
Cadena
Paralelogramo
Cable
Pares altos
Distancia grande
Distancia grande
---
---
Holguras
---
ruido
giro limitado
deformabilidad
Circular-lineal Tornillo sin fin
Cremallera
Poca holgura
Holgura media
Rozamiento
Rozamiento
Lineal- Circular Paral. Articulado
Cremallera
---
Holgura media
Control difícil
Rozamiento
Tabla 1.1.- Sistemas de transmisión para robots
Los reductores utilizados en robótica pueden tener diferentes morfologías y estar
basados en distintas tecnologías, y en muchas ocasiones vienen incorporados con el
actuador.
Actuadores
Para el estudio de los actuadores y sus modelos matemáticos se ha dedicado la
práctica cuatro de este libro. Sin embargo el lector debe conocer que los elementos
motrices que generan el movimiento de las articulaciones pueden ser, según la energía
que consuman, de tipo hidráulico, neumático, eléctrico o basado en las propiedades de
las aleaciones con memoria de forma (SMA).](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-8-320.jpg)


![Prácticas de Robótica utilizando Matlab®
Práctica 1 .- Pág. 10
Representación de la orientación
La orientación de un sólido en el espacio se puede especificar utilizando varios
sistemas de referencia. La orientación en el espacio tridimensional viene definida por
tres grados de libertad, luego será necesario un mínimo de tres parámetros linealmente
independientes.
En robótica es común el uso de matrices de rotación, debido a la comodidad
que proporciona el uso del álgebra matricial. La matriz de rotación es una matriz 3x3
ortogonal de cosenos directores que define la orientación del sistema OUVW móvil
respecto al sistema OXYZ fijo, y que tiene la forma siguiente:
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
wzvzuz
wyvyuy
wxvxux
kkjkik
kjjjij
kijiii
R
donde [ ]zyx kji son los vectores unitarios del sistema OXYZ y [ ]wvu kji los
vectores unitarios del sistema OUVW.
El ejemplo siguiente muestra la matriz de rotación del sistema OUVW que ha
girado un ángulo α respecto a OXYZ.
( )
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−=
αα
ααα
cos0
cos0
001
,
sen
senxR
Figura 1.11.- Rotación del sistema OUVW respecto al eje OX
Las matrices ortonormales de rotación pueden componerse para expresar la
aplicación continua de varias rotaciones (Recuerde el lector que el orden en que se
realizan las rotaciones es importante, pues el producto de matrices no es conmutativo).
También es común en robótica el uso de cuaternios, pero debido a que no se
utilizan en los desarrollos de las prácticas de este libro, no van a ser estudiados aquí.](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-11-320.jpg)





![Prácticas de Robótica utilizando Matlab®
Práctica 1 .- Pág. 16
Como todos los comandos de Matlab
la Robotics Toolbox nos ofrece ayuda en
línea en la que se puede conocer el uso de cada una de las funciones:
» help jtraj
JTRAJ Compute a joint space trajectory between two points
[Q QD QDD] = JTRAJ(Q0, Q1, N)
[Q QD QDD] = JTRAJ(Q0, Q1, N, QD0, QD1)
[Q QD QDD] = JTRAJ(Q0, Q1, T)
[Q QD QDD] = JTRAJ(Q0, Q1, T, QD0, QD1)
Returns a joint space trajectory Q from state Q0 to Q1. The number
of points is N or the length of the given time vector T. A 7th
order polynomial is used with default zero boundary conditions for
velocity and acceleration. Non-zero boundary velocities can be
optionally specified as QD0 and QD1.
The function can optionally return a velocity and acceleration
trajectories as QD and QDD.
Each trajectory is an mxn matrix, with one row per time step, and
one column per joint parameter.
»
La demo de Matlab
incluye gráficas de planificación de trayectorias y
animación alámbrica de robots donde se pueden visualizar los trayectorias calculadas.
Figura 1.17.- Ejecución de la demo de Robotics Toolbox](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-17-320.jpg)


![Prácticas de Robótica utilizando Matlab®
Práctica 2 .- Pág. 3
De acuerdo con la estructura del libro, todos los apartados presentan
herramientas desarrolladas en MatLab
para la solución de los problemas planteados.
2.2- Cinemática directa del brazo de un robot manipulador
Las técnicas que se estudian aquí, se aplican a un manipulador mecánico de
cadena abierta y tratan el estudio analítico y el modelado en MatLab
de la geometría
del movimiento de un robot con respecto a un sistema de referencia fijo como una
función del tiempo sin considerar la dinámica.
2.2.1 El problema cinemático directo
El problema cinemático directo se plantea en términos de encontrar una matriz
de transformación que relaciona el sistema de coordenadas ligado al cuerpo en
movimiento respecto a un sistema de coordenadas que se toma como referencia. Para
lograr esta representación se usan las matrices de transformación homogénea 4x4, la
cual incluye las operaciones de traslación y la orientación.
La matriz de transformación homogénea es una matriz de 4x4 que transforma un
vector expresado en coordenadas homogéneas desde un sistema de coordenadas hasta
otro sistema de coordenadas. Para una descripción más amplia acerca de las bases
algebraicas de las transformaciones homogéneas se recomienda estudiar las referencias:
[1] y [2].
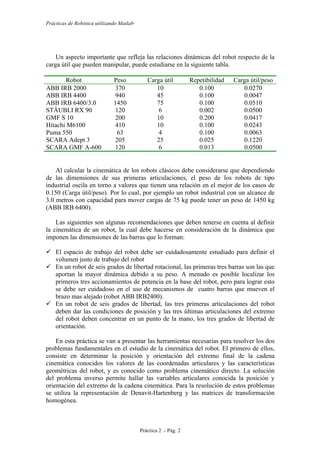
La matriz de transformación homogénea tiene la siguiente estructura:
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=⎥
⎦
⎤
⎢
⎣
⎡
=
1000
31 zzzz
yyyy
xxxx
x pasn
pasn
pasn
escaladof
posicióndevectorrotacióndematriz
T
⎥
⎦
⎤
⎢
⎣
⎡
=
1000
pasn
T
donde los vectores n, s, a, son vectores ortogonales unitarios y p es un vector que
describe la posición x, y, z del origen del sistema actual respecto del sistema de
referencia.
Para entender las propiedades de la matriz de transformación homogénea nos fijamos en
el siguiente gráfico.](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-21-320.jpg)


![Prácticas de Robótica utilizando Matlab®
Práctica 2 .- Pág. 6
Con base en la figura-2.2 y de acuerdo a las reglas de D-H, se determina la siguiente
matriz de transformación homogénea:
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡ −
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=−
0000
00
00
0001
1000
0100
0010
001
1000
0100
00
00
1000
100
0010
0001
1
ii
ii
i
ii
ii
i
i
i
cs
sc
a
cs
sc
d
A
αα
ααθθ
θθ
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
=−
1000
0
1
iii
iiiiiii
iiiiiii
i
i
dcs
sacsccs
cassscc
A
αα
θθαθαθ
θθαθαθ
Código en Matlab
. La función DENAVIT realiza los cálculos anteriores devolviendo
la matriz de transformación homogénea
% DENAVIT Matriz de transformación homogénea.
% DH = DENAVIT(TETA, D, A, ALFA) devuelve la matriz de transformacion
% homogénea 4 x 4 a partir de los parametros de Denavit-Hartenberg
% D, ALFA, A y TETA.
%
% See also DIRECTKINEMATIC.
function dh=denavit(teta, d, a, alfa)
dh=[cos(teta) -cos(alfa)*sin(teta) sin(alfa)*sin(teta) a*cos(teta);
sin(teta) cos(alfa)*cos(teta) -sin(alfa)*cos(teta) a*sin(teta);
0 sin(alfa) cos(alfa) d;
0 0 0 1];](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-24-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 2 .- Pág. 7
2.2.3 Representación de la cinemática directa de robots manipuladores
En esta sección se explican algunas arquitecturas de robots y como construir la
tabla de los parámetros de D-H. Para una información más detallada sobre este tema, se
recomienda estudiar las referencias [1] y [2].
Ejemplo 2.1
Figura-2.3 Parámetros de D-H para un robot cilíndrico
Eslabón θi di ai αi
1 θ1 l1 0 0
2 0 d2 - a2 -π/2
3 0 d3 0 0
4 θ4 l4 0 0
Tabla 2.1 Parámetros de D-H para el robot cilíndrico de la figura-2.3
• Note el lector el signo negativo del parámetro a2 así como la localización del origen
del sistema de coordenadas (x2, y2, z2)
• Las variables articulares son en este caso θ1, d2, d3, θ4
z1
θ1
x0
y0
z0
x1 y1
z2
y2
x2
x3
y3
l1
d2
d3
a2
l4
0
z4
1
2
3
4 θ4
x4
y4
z3](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-25-320.jpg)

![Prácticas de Robótica utilizando Matlab®
Práctica 2 .- Pág. 9
Código en Matlab
. La función DIRECTKINEMATIC resuelve la cinemática directa de
robots de cadena abierta. Para utilizarla debe invocarse junto con el vector de
coordenadas articulares Q de n componentes siendo n el número de eslabones del robot.
A continuación se muestra el código fuente utilizado para cada uno de los robots
que se están utilizando como ejemplos. El lector debe notar las modificaciones
realizadas en el código, debido al diferente número de eslabones de cada robot y a los
parámetros D-H de cada robot. Se recomienda que se realicen estos ejemplos como
práctica de los conocimientos adquiridos.
Ejemplo 2.3
Código fuente de la función DIRECTKINEMATIC para el robot cilíndrico de 4
grados de libertad del ejemplo 2.1
Debe notarse que el vector de coordenadas articulares Q representa los 4 grados
de libertad del robot, 2 rotacionales y 2 prismáticas y se introduce en los parámetros D-
H como variables.
Las dimensiones del robot, introducidas en los parámetros de D-H, son las
indicadas en el capítulo 1.
% DIRECTKINEMATIC4 Direct Kinematic.
% A04 = DIRECTKINEMATIC4(Q) devuelve la matriz de transformación del
% primer sistema de coordenadas al último en función del vector Q
% de variables articulares.
%
% See also DENAVIT.
function A04 = directkinematic4(q)
% Parámetros Denavit-Hartenberg del robot
teta = [q(1) 0 0 q(4)];
d = [0.4 q(2) q(3) 0.2 ];
a = [0 -0.1 0 0 ];
alfa = [0 -pi/2 0 0 ];
% Matrices de transformación homogénea entre sistemas de coordenadas
consecutivos
A01 = denavit(teta(1), d(1), a(1), alfa(1));
A12 = denavit(teta(2), d(2), a(2), alfa(2));
A23 = denavit(teta(3), d(3), a(3), alfa(3));
A34 = denavit(teta(4), d(4), a(4), alfa(4));
% Matriz de transformación del primer al último sistema de
coordenadas
A04 = A01 * A12 * A23 * A34;](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-27-320.jpg)

![Prácticas de Robótica utilizando Matlab®
Práctica 2 .- Pág. 11
% DIRECTKINEMATIC6 Direct Kinematic.
% A06 = DIRECTKINEMATIC6(Q) devuelve la matriz de transformación del
% primer sistema de coordenadas al último en función del vector Q
% de variables articulares.
%
% See also DENAVIT.
function A06 = directkinematic6(q)
% Parámetros Denavit-Hartenberg del robot
teta = q;
d = [0.315 0 0 0.5 0 0.08];
a = [0 0.45 0 0 0 0];
alfa = [-pi/2 0 pi/2 -pi/2 pi/2 0];
% Matrices de transformación homogénea entre sistemas de coordenadas
consecutivos
A01 = denavit(teta(1), d(1), a(1), alfa(1));
A12 = denavit(teta(2), d(2), a(2), alfa(2));
A23 = denavit(teta(3), d(3), a(3), alfa(3));
A34 = denavit(teta(4), d(4), a(4), alfa(4));
A45 = denavit(teta(5), d(5), a(5), alfa(5));
A56 = denavit(teta(6), d(6), a(6), alfa(6));
% Matriz de transformación del primer al último sistema de
coordenadas
A06 = A01 * A12 * A23 * A34 * A45 * A56;
A continuación se presenta la matriz obtenida para una configuración en la que todas las
coordenadas articulares tienen valor nulo:
» q=zeros(6,1)
q =
0
0
0
0
0
0
» T=directkinematic6(q)
T =
1.0000 0 0 0.4500
0 1.0000 0 0
0 0 1.0000 0.8950
0 0 0 1.0000](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-29-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 2 .- Pág. 12
2.3.- Cinemática inversa del brazo de un robot manipulador
La cinemática inversa consiste en hallar los valores de las coordenadas
articulares del robot [ ]T
nqqqq ,....,, 21= conocida la posición y orientación del extremo
del robot.
A pesar de que en la literatura [1] y [2] se pueden encontrar diversos métodos
genéricos para la resolución de la cinemática inversa que pueden ser implementados en
computadora, suele ser habitual la resolución por medio de métodos geométricos. La
mayor parte de los robots suelen tener cadenas cinemáticas relativamente sencillas, que
facilitan la utilización de los métodos geométricos. Para muchos robots, si se consideran
sólo los tres primeros grados de libertad, se tiene una estructura planar. Este hecho
facilita la resolución del problema. Asimismo los últimos tres grados de libertad suelen
usarse para la orientación de la herramienta, lo cual permite una resolución geométrica
desacoplada de la posición de la muñeca del robot y de la orientación de la herramienta.
En esta sección se va a resolver el problema cinemático inverso para los dos
robots anteriores, utilizando el método geométrico e implementándolo en Matlab
.
Ejemplo 2.5
Solución del robot cilíndrico de 4 grados de libertad.
En este caso particular, la solución geométrica es inmediata. Se parte de que la posición
del extremo del robot es conocida (px, py, pz) y se va a calcular los valores de las
coordenadas articulares.
Articulación 1
Para obtener el valor de θ1 (TETA1 en el código de Matlab
.) se proyecta el
punto del extremo del robot (px, py, pz) sobre el plano (x0, y0, z0) obteniendo una
sencilla relación angular. Sabiendo que θ1 es el ángulo entre x0 y x1, se obtienen las
siguientes gráficas.](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-30-320.jpg)

![Prácticas de Robótica utilizando Matlab®
Práctica 2 .- Pág. 14
Articulación 4
Para calcular la última articulación se necesita el cálculo previo del sistema de
referencia (x3, y3, z3), que se resolverá mediante la cinemática directa explicada en el
ejemplo 2.3. Dado que el vector a de aproximación es necesariamente paralelo a z4 se
deben cumplir las siguientes relaciones:
34 ·ynsin =θ
)cos,(2 444 θθθ sinatan=
34 ·cos ys=θ
Código en Matlab
. La función INVERSEKINEMATIC4 resuelve la cinemática inversa
del robot cilíndrico de 4 gdl. Para ello toma como parámetros la matriz homogénea T,
que representa la orientación y posición del extremo del robot y devuelve el vector de
coordenadas articulares.
% Q = INVERSEKINEMATIC4(T) devuelve el vector de coordenadas
% articulares correspondiente a la solución cinemática inversa de
% la mano del manipulador en la posición y orientación expresadas
% en la matriz T.
%
% See also DIRECTKINEMATIC4, DENAVIT.
function q = inversekinematic4(T)
p = T(1:3,4); % Posición de la mano del manipulador
% Inicialización de las variables articulares a calcular
q1 = 0;
q2 = 0;
q3 = 0;
q4 = 0;
% Parámetros Denavit-Hartenberg del robot
teta = [q1 0 0 q4 ];
d = [0.4 q2 q3 0.2];
a = [0 -0.1 0 0 ];
alfa = [0 -pi/2 0 0 ];
% Solución de la primera articulación: q1
R = sqrt(p(1)^2+p(2)^2);
r = sqrt(R^2-a(2)^2);
sphi = -p(1)/R;
cphi = p(2)/R;
phi = atan2(sphi, cphi);
y3
x4
x3
θ4
donde n y s son vectores de orientación del extremo
del robot.](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-32-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 2 .- Pág. 15
sbeta = -a(2)/R;
cbeta = r/R;
beta = atan2(sbeta, cbeta);
q1 = phi - beta;
% Solución de la segunda articulación: q2
q2 = p(3) - d(1);
% Solución de la tercera articulación: q3
q3 = r - d(4);
% Solución de la cuarta articulación: q4
% Cálculo de la matriz de transformación A03
A01 = denavit(q1, d(1), a(1), alfa(1));
A12 = denavit(teta(2), q2, a(2), alfa(2));
A23 = denavit(teta(3), q3, a(3), alfa(3));
A03 = A01 * A12 * A23;
y3 = A03(1:3,2);
sq4 = dot(T(1:3,1), y3); % Vector orientación n: T(1:3,1)
cq4 = dot(T(1:3,2), y3); % Vector orientación s: T(1:3,2)
q4 = atan2(sq4, cq4);
% Vector de variables articulares
q = [q1 q2 q3 q4]';
⇒ Se observa como la cinemática directa está incluida en los cálculos necesarios
para obtener la matriz 0
A3.
En el ejemplo mostrado a continuación se puede comprobar como después de
asignar un vector de coordenadas articulares aleatorio, y obtener la matriz homogénea
del extremo de robot correspondiente a este vector, si sobre esta matriz se aplica la
función INVERSEKINEMATIC4 se obtiene el vector q original.](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-33-320.jpg)

![Prácticas de Robótica utilizando Matlab®
Práctica 2 .- Pág. 17
debajo o por encima de la articulación 2, para lograr una misma posición de la muñeca.
Asimismo, la MUÑECA puede tomar también dos configuraciones distintas, MUÑECA
ARRIBA y MUÑECA ABAJO, para obtener una misma orientación del efector final.
Debido a las anteriores consideraciones, es necesario introducir en la resolución del
problema cinemático inverso dos parámetros, llamados por similitud CODO y
MUÑECA, que representen las cuatro posibles configuraciones que puede adoptar el
robot cuando se le solicita alcanzar una posición y orientación determinadas.
Para una descripción más amplia acerca de la resolución del problema cinemático
inverso se recomienda estudiar las referencias: [1] y [2].
Figura-2.6 Cinemática inversa del robot de 6 gdl.
A continuación se muestra la solución geométrica del robot estudiado y su
implementación en Matlab
.
⇒ Se recomienda seguir las explicaciones con el código fuente de la función
INVERSEKINEMATIC6.
Problema de posición. Cálculo de las tres primeras articulaciones.
Articulación 1
22
yx ppR +=
R
p
sin
y
=1θ
R
px
=1cosθ
)cos,(2 111 θθθ sinatan=
MUÑECA
px, py, pzCODO
a
s
n
y0
x0
z0
R
c
px,py
θ1](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-35-320.jpg)

![Prácticas de Robótica utilizando Matlab®
Práctica 2 .- Pág. 19
Articulación 3
Al igual que en la articulación 2, se debe tener en cuenta las dos posibles
configuraciones del codo.
β
π
θ −=
2
3
3
2
3
π
βθ −=
Problema de orientación. Cálculo de las tres últimas articulaciones.
Conocidos los tres primeros ángulos θ1, θ2 y θ3 se resuelve la cinemática directa para
los tres primeros eslabones, obteniéndose la matriz 0
A3 necesaria para la resolución de
las últimas tres articulaciones. Siguiendo la referencia [1], para resolver el problema de
la orientación se han de conseguir que las tres últimas articulaciones cumplan los
criterios siguientes:
1. Establecer la articulación 4 de forma tal que una rotación respecto de la
rotación 5 alineará el eje de movimiento de la articulación 6 con el vector de
aproximación dado (a).
2. La articulación 5 alineará el eje de movimiento de la articulación 6 con el
vector de aproximación.
3. Fijar la articulación 6 para alinear el vector de orientación dado (s) (o el de
deslizamiento (n)) y el vector normal.
Matemáticamente, estos criterios significan:
1.
( )
xaz
xaz
z
3
3
4
±
=
2. a = z5
3. s = y6
Ambas orientaciones de la muñeca (ARRIBA y ABAJO) se definen observando la
orientación del sistema de coordenadas de la mano (n,s,a) con respecto al sistema de
coordenadas (x5, y5, z5). Para analizar las configuraciones de MUÑECA ARRIBA y
MUÑECA ABAJO, se utiliza un parámetro de orientación Ω (omega en el código de
Matlab
) que hace referencia a la orientación del vector unitario n (o s) con respecto al
vector unitario x5 (o y5) y que viene definido en la referencia Fu [1] como:
0 si se está en el caso degenerado
Ω= s·y5 si s·y5 ≠0
n·y5 si s·y5=0
l2
l1
l3
x2
x3
β
θ3
l2
l1
l3
x2
x3
β
θ3](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-37-320.jpg)

![Prácticas de Robótica utilizando Matlab®
Práctica 2 .- Pág. 21
Código en Matlab
.La función INVERSEKINEMATIC6 resuelve la cinemática inversa
del robot rotacional de 6 gdl. Para ello toma como parámetros la matriz homogénea T,
y los parámetros CODO y MUÑECA para definir las posibles configuraciones. Ha de
tenerse en consideración que determinados puntos y orientaciones que pertenezcan al
espacio de trabajo del robot, no podrán alcanzarse con algunas configuraciones. Por
ello se recomienda al lector que trate de experimentar con estos puntos extremos con la
herramienta que a continuación se presenta, y analice los resultados.
% INVERSEKINEMATIC6 Inverse Kinematic
% Q = INVERSEKINEMATIC6(T, CODO, MUNECA) devuelve el vector de coordenadas
% articulares correspondiente a la solución cinemática inversa de la mano
% del manipulador en la posición y orientación expresadas en la matriz T.
% CODO = 1 indica codo del robot arriba, es decir, que la articulación 3 se
% sitúa por encima de la articulación 2, mientras que CODO = -1 indica codo
% abajo, es decir que la articulación 2 se sitúa por encima de la 3.
% MUNECA = 1 indica que la muñeca del robot se sitúa por debajo de la
coordenada
% expresada en T, mientras que MUNECA = -1 significa que la muñeca se sitúa
% por arriba.
%
% See also DIRECTKINEMATIC6, DENAVIT.
function q = inversekinematic6(T,codo,muneca)
% Parámetros Denavit-Hartenberg del robot
d = [0.315 0 0 0.5 0 0.08];
a = [0 0.45 0 0 0 0];
alfa = [-pi/2 0 pi/2 -pi/2 pi/2 0];
% Posición de la mano del manipulador
p = T(1:3,4)-d(6)*T(1:3,3);
% Solución de la primera articulación: q1
R = sqrt(p(1)^2+p(2)^2);
sq1=p(2)/R;
cq1=p(1)/R;
q1 = atan2(sq1,cq1);
% Solución de la segunda articulación: q2
r = sqrt(R^2+(p(3)-d(1))^2);
salfa = (d(1)-p(3))/r;
calfa = R/r;
cbeta = (r^2+a(2)^2-d(4)^2)/(2*r*a(2));
sbeta = sqrt(1-cbeta^2);
if codo == -1 % Codo abajo
sq2 = salfa*cbeta+sbeta*calfa;
cq2 = calfa*cbeta-salfa*sbeta;
else % Codo arriba
sq2 = salfa*cbeta-sbeta*calfa;
cq2 = calfa*cbeta+salfa*sbeta;
end
q2 = atan2(sq2,cq2);
% Solución de la tercera articulación: q3
cbeta=(a(2)^2+d(4)^2-r^2)/(2*a(2)*d(4));
sbeta=sqrt(1-cbeta^2);
beta=atan2(sbeta,cbeta);](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-39-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 2 .- Pág. 22
if codo == 1 % Codo arriba
q3 = 3*pi/2-beta;
else % Codo abajo
q3 = beta - pi/2;
end
% Solución de la cuarta articulación: q4
% Cálculo de la matriz de transformación A03
A01 = denavit(q1, d(1), a(1), alfa(1));
A12 = denavit(q2, d(2), a(2), alfa(2));
A23 = denavit(q3, d(3), a(3), alfa(3));
A03 = A01 * A12 * A23;
x3 = A03(1:3,1);
y3 = A03(1:3,2);
z3 = A03(1:3,3);
z4 = cross(z3,T(1:3,3)); % Vector orientación a: T(1:3,3)
% Determinación del indicador de orientación omega
aux = dot(T(1:3,2),z4); % Vector orientación s: T(1:3,2)
if aux ~= 0
omega = aux;
else
aux=dot(T(1:3,1),z4); % Vector orientación n: T(1:3,1)
if aux ~=0
omega=aux;
else
omega=0;
end
end
M = muneca*sign(omega);
sq4 = -M*dot(z4,x3);
cq4 = M*dot(z4,y3);
q4 = atan2(sq4,cq4);
% Solución de la quinta articulación: q5
z5 = T(1:3,3); % Vector de orientación a: T(1:3,3)
A34 = denavit(q4, d(4), a(4), alfa(4));
A04 = A03 * A34;
x4 = A04(1:3,1);
y4 = A04(1:3,2);
sq5 = dot(T(1:3,3),x4); % Vector de orientación a: T(1:3,3)
cq5 = -dot(T(1:3,3),y4); % Vector de orientación a: T(1:3,3)
q5 = atan2(sq5,cq5);
% Solución de la sexta articulación: q6
y6 = T(1:3,2); % Vector de orientación s: T(1:3,2)
A45 = denavit(q5, d(5), a(5), alfa(5));
A05 = A04 * A45;
y5 = A05(1:3,2);
sq6 = dot(T(1:3,1),y5); % Vector de orientación n: T(1:3,1)
cq6 = dot(T(1:3,2),y5); % Vector de orientación s: T(1:3,2)
q6 = atan2(sq6,cq6);
% Vector de coordenadas articulares
q = [q1 q2 q3 q4 q5 q6]';](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-40-320.jpg)

![Prácticas de Robótica utilizando Matlab®
Práctica 2 .- Pág. 24
Ejemplo 2.7
Código en Matlab
. La función DRAWROBOT3D realiza una representación 3D de un
robot en función del vector de variables articulares Q
Particularizando DRAWROBOT3D para los ejemplos anteriores se obtiene las
funciones que se han llamado DRAWROBOT3D4 y DRAWROBOT3D6.
% DRAWROBOT3D4 Representación 3D de un robot.
% DRAWROBOT3D4(Q) realiza una representación 3D de un robot
% en función del vector de variables articulares Q.
%
% See also DENAVIT, DIRECTKINEMATIC4.
function drawrobot3d4(q)
% Parámetros Denavit-Hartenberg del robot
teta = [q(1) 0 0 q(4)];
d = [0.4 q(2) q(3) 0.2 ];
a = [0 -0.1 0 0 ];
alfa = [0 -pi/2 0 0 ];
% Matrices de transformación homogénea entre sistemas de coordenadas
consecutivos
A01 = denavit(teta(1), d(1), a(1), alfa(1));
A12 = denavit(teta(2), d(2), a(2), alfa(2));
A23 = denavit(teta(3), d(3), a(3), alfa(3));
A34 = denavit(teta(4), d(4), a(4), alfa(4));
% Matrices de transformación del primer sistema al correspondiente
A02 = A01 * A12;
A03 = A02 * A23;
A04 = A03 * A34;
% Vector de posicion (x, y, z) de cada sistema de coordenadas
x0 = 0; y0 = 0; z0 = 0;
x1 = A01(1,4); y1 = A01(2,4); z1 = A01(3,4);
xi = x1; yi = y1; zi = z1 + d(2);
x2 = A02(1,4); y2 = A02(2,4); z2 = A02(3,4);
x3 = A03(1,4); y3 = A03(2,4); z3 = A03(3,4);
x4 = A04(1,4); y4 = A04(2,4); z4 = A04(3,4);
% Se dibuja el robot
x = [x0 x1 xi x2 x3 x4];
y = [y0 y1 yi y2 y3 y4];
z = [z0 z1 zi z2 z3 z4];
plot3(x,y,z);
% Se coloca una rejilla a los ejes
grid;
% Se establecen los límites de los ejes
axis([-1.5 1.5 -1.5 1.5 0 1.5]);
Si se representa la configuración en la que todas las coordenadas articulares son
nulas, se obtiene el siguiente dibujo:](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-42-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 2 .- Pág. 25
Ejemplo 2.8
Se presenta ahora el código y la representación gráfica del robot rotacional de 6
grados de libertad.
% DRAWROBOT3D6 Representación 3D de un robot.
% DRAWROBOT3D6(Q) realiza una representación 3D de un robot
% en función del vector de variables articulares Q.
%
% See also DENAVIT, DIRECTKINEMATIC6.
function drawrobot3d6(q)
% Parámetros Denavit-Hartenberg del robot
teta = q;
d = [0.315 0 0 0.5 0 0.08];
a = [0 0.45 0 0 0 0 ];
alfa = [-pi/2 0 pi/2 -pi/2 pi/2 0 ];
% Matrices de transformación homogénea entre sistemas de coordenadas
consecutivos
A01 = denavit(teta(1), d(1), a(1), alfa(1));
A12 = denavit(teta(2), d(2), a(2), alfa(2));
A23 = denavit(teta(3), d(3), a(3), alfa(3));
A34 = denavit(teta(4), d(4), a(4), alfa(4));
A45 = denavit(teta(5), d(5), a(5), alfa(5));
A56 = denavit(teta(6), d(6), a(6), alfa(6));](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-43-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 2 .- Pág. 26
% Matrices de transformación del primer sistema al correspondiente
A02 = A01 * A12;
A03 = A02 * A23;
A04 = A03 * A34;
A05 = A04 * A45;
A06 = A05 * A56;
% Vector de posicion (x, y, z) de cada sistema de coordenadas
x0 = 0; y0 = 0; z0 = 0;
x1 = A01(1,4); y1 = A01(2,4); z1 = A01(3,4);
x2 = A02(1,4); y2 = A02(2,4); z2 = A02(3,4);
x3 = A03(1,4); y3 = A03(2,4); z3 = A03(3,4);
x4 = A04(1,4); y4 = A04(2,4); z4 = A04(3,4);
x5 = A05(1,4); y5 = A05(2,4); z5 = A05(3,4);
x6 = A06(1,4); y6 = A06(2,4); z6 = A06(3,4);
% Se dibuja el robot
x = [x0 x1 x2 x3 x4 x5 x6];
y = [y0 y1 y2 y3 y4 y5 y6];
z = [z0 z1 z2 z3 z4 z5 z6];
plot3(x,y,z);
% Se coloca una rejilla a los ejes
grid;
% Se establecen los límites de los ejes
axis([-1 1 -1 1 0 1.5]);
Si se representa la configuración en la que todas las coordenadas articulares son
nulas, se obtiene el siguiente dibujo:](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-44-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 2 .- Pág. 27
2.5.- PRACTICA. Animación de los robots.
En este apartado se va a realizar un sencillo ejemplo de utilización de las funciones
estudiadas hasta ahora. Se trata de colocar al robot en dos posiciones distintas y animar
una trayectoria recta entre esas dos configuraciones. Para ello se deberán generar varias
posiciones intermedias.
Se utiliza la función planifica(p1,p2,ni) en la que se introducen las coordenadas
cartesianas de los puntos inicial y final y el número de puntos intermedios.
Ejemplo 2.9
En este ejemplo se utiliza la cinemática inversa del robot rotacional de 6 gdl para
trazar una línea recta entre un punto p1 inicial y un punto p2 final. El número de puntos
intermedios es variable.
Se ha utilizado la función PLANIFICA6(P1,P2,N,S,A,CODO,MUÑECA,NPUNTOS)
en el que se introduce las coordenadas cartesianas de los puntos inicial y final, la
orientación (n,s,a) del punto final, los parámetros CODO y MUÑECA para seleccionar
la configuración del robot y el número de puntos intermedio. Esta función proporciona
una matriz de (npuntos+2) columnas por 6 filas que se utilizará por la función
ANIMACION6(MAT_Q) para dibujar la trayectoria entre los dos puntos.
Código en Matlab
. La función PLANIFICA6(P1,P2,N,S,A,CODO,MUÑECA,
NPUNTOS) calcula la matriz de coordenadas articulares utilizada para graficar el
movimiento del robot.
% PLANIFICA6 Planificación de trayectorias
% MAT_Q = PLANIFICA6(P1, P2, N, S, A, CODO, MUNECA, NPUNTOS) realiza
% una planificación de trayectoria en línea recta desde la coordenada
% cartesiana P1 hasta la P2, de manera que la mano del manipulador
% posee la orientación expresada por [N S A]. CODO = 1 indica codo del
% robot arriba, es decir, que la articulación 3 se sitúa por encima de
% la articulación 2, mientras que CODO = -1 indica codo abajo, es decir
% que la articulación 2 se sitúa por encima de la 3. MUNECA = 1 indica que
% la muñeca del robot se sitúa por debajo de la coordenada cartesiana,
% mientras que MUNECA = -1 significa que la muñeca se sitúa por arriba.
% NPUNTOS indica el número de puntos en los que se divide la trayectoria.
% En MAT_Q se devuelve las coordenadas articulares, almacenadas por
% columnas, correspondientes a cada uno de los puntos cartesianos en los
% que se divide la trayectoria. MAT_Q es una matriz de NPUNTOS + 2 columnas
% y 6 filas.
%
% See also INVERSEKINEMATIC6.
function mat_q = planifica6(p1, p2, n, s, a, codo, muneca, npuntos)
% Cálculo del vector unitario
u = p2-p1;
mu = sqrt(u(1)^2+u(2)^2+u(3)^2);
u = (1/mu)*u;
% Cálculo de la distancia entre puntos
d = mu/(npuntos+1);](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-45-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 2 .- Pág. 28
for i=0:(npuntos+1)
% Cálculo de la posición cartesiana actual de la mano del
manipulador
p = p1+(i*d)*u;
T = [n s a p];
% Cálculo de las coordenadas articulares
q = inversekinematic6(T,codo,muneca);
mat_q(:,i+1) = q;
end
Utilizando ahora la función ANIMACION6(MAT_Q) se presenta el movimiento del
robot entre los 2 puntos especificados.
% ANIMACION6 Animación de la trayectoria de un robot
% ANIMACION(MAT_Q) realiza la animación de la trayectoria, expresada
% en la matriz MAT_Q, de un brazo robot de 6 GDL. MAT_Q contiene 6 filas
% y una columna para cada disposición del robot.
%
% See also PLANIFICA6, DRAWROBOT3D6.
function animacion6(mat_q)
% Parámetros Denavit-Hartenberg del robot
d = [0.315 0 0 0.5 0 0.08];
a = [0 0.45 0 0 0 0 ];
alfa = [-pi/2 0 pi/2 -pi/2 pi/2 0 ];
% Vector de posicion (x, y, z) del sistema de coordenadas de
referencia
x0 = 0; y0 = 0; z0 = 0;
% Se dibuja el sistema de coordenadas de referencia. Se asigna el modo
XOR para borrar
% sólo el robot dibujado anteriormente. Se utiliza un grosor de línea
de 2 unidades
p = plot3(x0,y0,z0,'EraseMode','xor','LineWidth',2);
% Se asigna una rejilla a los ejes
grid;
% Se establecen los límites de los ejes
axis([-1 1 -1 1 0 1.5]);
% Mantiene el gráfico actual
hold on;
% Número de columnas de la matriz
n = size(mat_q,2);
% Se dibuja la disposición del robot correspondiente a cada columna
for i=1:n
% Variables articulares del brazo robot
teta1 = mat_q(1,i);
teta2 = mat_q(2,i);
teta3 = mat_q(3,i);
teta4 = mat_q(4,i);
teta5 = mat_q(5,i);
teta6 = mat_q(6,i);](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-46-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 2 .- Pág. 29
% Matrices de transformación homogénea entre sistemas de coordenadas
consecutivos
A01 = denavit(teta1, d(1), a(1), alfa(1));
A12 = denavit(teta2, d(2), a(2), alfa(2));
A23 = denavit(teta3, d(3), a(3), alfa(3));
A34 = denavit(teta4, d(4), a(4), alfa(4));
A45 = denavit(teta5, d(5), a(5), alfa(5));
A56 = denavit(teta6, d(6), a(6), alfa(6));
% Matrices de transformación del primer sistema al correspondiente
A02 = A01 * A12;
A03 = A02 * A23;
A04 = A03 * A34;
A05 = A04 * A45;
A06 = A05 * A56;
% Vector de posicion (x, y, z) de cada sistema de coordenadas
x1 = A01(1,4); y1 = A01(2,4); z1 = A01(3,4);
x2 = A02(1,4); y2 = A02(2,4); z2 = A02(3,4);
x3 = A03(1,4); y3 = A03(2,4); z3 = A03(3,4);
x4 = A04(1,4); y4 = A04(2,4); z4 = A04(3,4);
x5 = A05(1,4); y5 = A05(2,4); z5 = A05(3,4);
x6 = A06(1,4); y6 = A06(2,4); z6 = A06(3,4);
% Se dibuja el robot
x = [x0 x1 x2 x3 x4 x5 x6];
y = [y0 y1 y2 y3 y4 y5 y6];
z = [z0 z1 z2 z3 z4 z5 z6];
set(p,'XData',x,'YData',y,'ZData',z);
% Se fuerza a MATLAB a actualizar la pantalla
drawnow;
end
⇒ Notar que la función plot3 ha permitido dibujar sobre la animación la trayectoria
seguida por el extremo del robot.](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-47-320.jpg)

![Prácticas de Robótica utilizando Matlab®
Práctica 3 .- Pág. 1
Práctica 3
Dinámica de Robots
3.1.-Introducción
La dinámica del robot relaciona el movimiento del robot y las fuerzas implicadas
en el mismo. El modelo dinámico establece relaciones matemáticas entre las
coordenadas articulares (o las coordenadas del extremo del robot), sus derivadas
(velocidad y aceleración), las fuerzas y pares aplicados en las articulaciones (o en el
extremo) y los parámetros del robot (masas de los eslabones, inercias, etc).
Siguiendo con la filosofía de este libro, se recomienda al lector que quiera
profundizar sobre la dinámica de robots, la lectura de los textos [1],[2],[3], donde se
estudian varias formulaciones clásicas como Lagrange-Euler o las ecuaciones
generalizadas de D’Alembert. Hay que tener en cuenta que las ecuaciones de
movimiento obtenidas con estas formulaciones son equivalentes en el sentido que
describen la conducta dinámica del robot, sin embargo, cada una de ellas presenta
características diferentes que la hacen más apropiada para ciertas tareas. Por ejemplo, la
formulación de Lagrange-Euler presenta un modelo simple y elegante, dando como
resultado una serie de ecuaciones diferenciales no lineales de 2º orden acopladas útiles
para el estudio de estrategias de control en el espacio de estados de las variables
articulares del robot, pero que se presentan ineficaces para aplicaciones en tiempo real
dado el elevado tiempo de computación que requieren las operaciones con matrices de
transformación homogénea.
Los modelos dinámicos que se estudian en esta práctica están basados en el
algoritmo recursivo de Newton-Euler (N-E) desarrollado por Luh [1]. Aunque las
formulaciones recursivas destruyen la estructura del modelo dinámico analítico y dan
lugar a la falta de ecuaciones cerradas necesarias para el análisis del control, la
dificultad de un análisis clásico es enorme debido a que se obtienen expresiones
fuertemente no-lineales que constan de cargas inerciales, fuerzas de acoplo entre las
articulaciones y efectos de las cargas de gravedad, con la dificultad añadida de que los
pares/fuerzas dinámicos dependen de los parámetros físicos del manipulador, de la
configuración instantánea de las articulaciones, de la velocidad, de la aceleración y de la](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-49-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 3 .- Pág. 2
carga que soporta el robot. Aunque las ecuaciones del movimiento son equivalentes ya
sean analíticas o recursivas, los diferentes planteamientos dependen de los objetivos que
se quieran conseguir con ellos. En algunos casos es necesario solucionar el problema
dinámico de un robot para lograr tiempos de calculo rápidos en la evaluación de los
pares y fuerzas articulares para controlar el manipulador, y en otros casos son necesarios
planteamientos para facilitar el análisis y la síntesis del control.
3.2.-Dinámica inversa. La formulación de Newton-Euler
El método de Newton-Euler permite obtener un conjunto de ecuaciones
recursivas hacia delante de velocidad y aceleración lineal y angular las cuales están
referidas a cada sistema de referencia articular. Las velocidades y aceleraciones de cada
elemento se propagan hacia adelante desde el sistema de referencia de la base hasta el
efector final. Las ecuaciones recursivas hacia atrás calculan los pares y fuerzas
necesarios para cada articulación desde la mano (incluyendo en ella efectos de fuerzas
externas), hasta el sistema de referencia de la base.
3.2.1. Sistemas de coordenadas en movimiento.
La formulación de N-E se basa en los sistemas de coordenadas en movimiento
[1].
Figura 3.1. Sistemas de coordenadas en movimiento
Con respecto a la figura 3.1 se tiene que el sistema de coordenadas 0*
se desplaza y gira
en el espacio respecto del sistema de referencia de la base 0, el vector que describe el
origen del sistema en movimiento es h y el punto P se describe respecto del sistema 0*
a
través del vector r*
, de acuerdo a esto, la descripción del punto P respecto del sistema
de la base es:
hrr += *
(3.1)
hvv
dt
dh
dt
dr
dt
dr
+=+= *
*
(3.2)
donde ν*
es la velocidad del punto P respecto del origen del sistema 0*
en movimiento y
νh es la velocidad del origen del sistema 0*
respecto de la base.
y0
h
r*
0*
y*
x*
z*
0
r
x0
P
z0](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-50-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 3 .- Pág. 3
Si el punto P se desplaza y gira respecto del sistema 0*
la ecuación (3.2) debe escribirse
como:
dt
dh
rw
dt
rd
dt
dh
dt
dr
v +⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
×+=+= *
***
(3.3)
donde
dt
rd **
es la velocidad lineal del punto P respecto del origen 0*
y *
rw× es la
velocidad angular del punto P respecto del origen 0*
.[1]
De manera similar la aceleración general del sistema de puede describir como:
haa
dt
hd
dt
rd
dt
dv
a +=+== *
2
2
2
*2
(3.4)
( ) 2
2
*
**
2
*2*
2
dt
hd
r
dt
dw
rww
dt
rd
w
dt
rd
a +×+××+×+= (3.5)
3.2.2. Cinemática de los eslabones del Robot.
A partir de las ecuaciones (3.1) a (3.5) de la sección anterior se desarrolla a
continuación el planteamiento general para la cinemática de los eslabones del robot [1]
Figura 3.2. Relaciones vectoriales entre los sistemas de referencia 0,0*
y 0’
De acuerdo a la figura 3.2 las ecuaciones cinemáticas para los eslabones de un robot, se
pueden escribir como:
1
*
1
**
−− +×+= iii
i
i vpw
dt
pd
v (3.6)
*
1 iii www += −
0 y0
z0
x0
zi-1
zi-2
zi
xi
yi
pi
pi-1
0*
yi-1
xi-1
ai-1
ai
0’
p*
i
αi
θi
articulación
i-1
articulación i
articulación
i+1](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-51-320.jpg)


![Prácticas de Robótica utilizando Matlab®
Práctica 3 .- Pág. 6
3.2.3. Ecuaciones de movimiento recursivas.
A partir de las ecuaciones cinemáticas del apartado anterior y aplicando el principio de
D’Alembert del equilibrio estático para todos los instantes de tiempo, se obtienen las
ecuaciones recursivas de Newton-Euler.[1]
Si se utiliza la nomenclatura de la figura 3.2 sobre un eslabón cualquiera del robot, tal y
como se muestra en la figura 3.3
Figura 3.3.Fuerzas y momentos sobre el elemento i
Donde:
im masa total del eslabón i,
ir posición del centro de masa del elemento i desde el origen del
sistema de referencia de la base,
is posición del centro de masa del elemento i desde el origen del
sistema de coordenadas (xi, yi, zi),
*
ip posición del origen de coordenadas i-ésimo con respecto al
sistema de coordenadas (i-1)-ésimo,
dt
rd
v i
i = velocidad lineal del centro de masa del elemento i,
dt
vd
a i
i = aceleración lineal del centro de masa del elemento i,
iF fuerza total externa ejercida sobre el elemento i en el centro de
masa,
iN momento total externo ejercido sobre el elemento i en el centro de
masa,
iI matriz de inercia del elemento i respecto de su centro de masa con
respecto al sistema de coordenadas (x0, y0, z0),
Centro de masa del elemento i
O’
is
ir
1
*
−−=+ iiii prsp
*
ip
O*
ni+1
fi+1
y0
x0
z0
ni
fi
pi-1
pi
(xi, yi, zi)(xi-1, yi-1, zi-1)
Elemento i+1
Elemento i-1](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-54-320.jpg)

![Prácticas de Robótica utilizando Matlab®
Práctica 3 .- Pág. 8
3.2.4. Algoritmo computacional.
En resumen de los dos apartados anteriores, las ecuaciones de N-E consisten en un
conjunto de ecuaciones recursivas [(3.13),(3.14), (3.17), (3.18)] hacia delante y
[(3.18),(3.19), (3.20), (3.21),(3.26)] hacia atrás.
Para obtener un algoritmo computacional, se debe tener en cuenta que en las anteriores
ecuaciones, las matrices de inercia iI y los parámetros del robot, ir , is , *
ip están
referenciados respecto del sistema de coordenadas de la base.
Luh y col. [1980] utilizaron las matrices de rotación 3x3 i
i
R1−
, que ya han sido
estudiadas en la práctica 2 pues corresponden a la submatriz superior izquierda de las
matrices de transformación homogénea i
i
A1−
, para expresar las variables
iw , iw , iv , iv , ia ,
*
ip , is , iF , iN , if , in y iτ que se refieren al sistema de coordenadas de
la base como i
i
wR0 , i
i
wR 0 , i
i
vR0 , i
i
vR 0 , i
i
aR0 ,
*
0 i
i
pR , i
i
sR0 , i
i
FR0 , i
i
NR0 , i
i
fR0 , i
i
nR0 y
i
i
R τ0 , que están referenciados al propio sistema de coordenadas del elemento i.
De esta manera, las ecuaciones recursivas de N-E quedan expresadas en la siguiente
tabla:](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-56-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 3 .- Pág. 9
Ecuaciones hacia delante: i = 1,2,....,n
)( 010
1
1 ii
i
i
i
qzwRR +−
−
− si el eslabón i es rotacional
i
i
wR0 = (3.27)
)( 10
1
1 −
−
− i
i
i
i
wRR si el eslabón i es traslacional
( ) ]ii
i
ii
i
i
i
qzwRqzwRR 010
1
010
1
1 )([ ×++ −
−
−
−
− si el eslabón i es rotacional
i
i
wR 0 = (3.28)
)( 10
1
1 −
−
− i
i
i
i
wRR si el eslabón i es traslacional
[ ]
( )10
1
1
*
000
*
00 )()()()()(
−
−
−+
+××+×
i
i
i
i
i
i
i
i
i
i
i
i
i
i
vRR
pRwRwRpRwR
si el eslabón i es rotacional
i
i
vR 0 = (3.29)
[ ])()()(
)()(2
)()()(
*
000
010
*
0010
1
01
i
i
i
i
i
i
ii
i
i
i
i
i
i
i
i
i
ii
i
pRwRwR
qzRwR
pRwRvRqzR
××+
+×+
+×++
−
−
−
−
si el eslabón i es traslacional
( ) ( ) ( ) ( ) ( )[ ] i
i
i
i
i
i
i
i
i
i
i
i
i
i
vRsRwRwRsRwRaR 0000000 +××+×= (3.30)
Ecuaciones hacia atrás: i =n,n-1,....,1
i
i
ii
i
i
i
i
i
aRmfRRfR 010
1
10 )( += +
+
+ (3.31)
]
( )( ) ( ) ( )( )[ ]i
i
ii
i
i
i
i
i
ii
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
wRRIRwRwRRIR
FRsRpRfRpRnRRnR
0
0
000
0
0
00
*
010
1*
0
1
10
1
10 )()()()([
×++
+×++×+= +
++
+
+
+
(3.32)
iii
iTi
qbzRnR i
+− )()( 010
si el eslabón i es rotacional
i
i
R τ0 = (3.33)
iii
iT
i
i
qbzRfR +− )()( 010 si el eslabón i es traslacional
Tabla 3.1. Algoritmo recursivo de N-E](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-57-320.jpg)


![Prácticas de Robótica utilizando Matlab®
Práctica 3 .- Pág. 12
% NEWTONEULER4 Dinámica inversa utilizando el método de Newton-
Euler.
% TAU = NEWTONEULER4(Q, QP, QPP, G, M5, IEXTER) calcula el vector
% 4x1 de pares/fuerzas de entrada a las articulaciones. Q el vector
% 4x1 de coordenadas articulares. QP es el vector 4x1 que representa
% la velocidad de cada articulación. QPP es el vector 4x1 que indica
% la aceleración de cada articulación. G es el valor de la gravedad
(m/s^2).
% M5 es la masa de la carga externa(Kg) que transporta el brazo robot.
% IEXTER es la matriz 3x3 de inercia de la carga exterior(Kg-m^2).
%
% See also DH, RI0PI, RI0SI, RI0WI, RI0WIP, RI0VPI_R, RI0AI, RI0FI, RI0NI,
% RI0FIA, RI0NIA, T_R, F_P.
function tau = newtoneuler4(q,qp,qpp,g,m5,Iexter);
% ------------------------------------------------------------
% Parámetros Denavit-Hartenberg del robot
% ------------------------------------------------------------
teta = [q(1) 0 0 q(4)];
d = [0.4 q(2) q(3) 0.2 ];
a = [0 -0.1 0 0 ];
alfa = [0 -pi/2 0 0 ];
% ------------------------------------------------------------
% Factores de posicionamiento de los centros de gravedad
% ------------------------------------------------------------
factor1 = -0.5; factor2 = -0.5; factor3 = -0.5; factor4 = -0.5;
% ------------------------------------------------------------
% Masa de cada elemento (Kg)
% ------------------------------------------------------------
m1 = 10; m2 = 5; m3 = 5; m4 = 3;
% ------------------------------------------------------------
% Coeficiente de rozamiento viscoso de cada articulacion
% ------------------------------------------------------------
b1 = 0.05; b2 = 0.05; b3 = 0.05; b4 = 0.05;
% ------------------------------------------------------------
% Matrices de Inercia (Kg-m^2)
% ------------------------------------------------------------
r10I_r01 = [0.0191 0 0;0 0.0191 0;0 0 0.0068];
r20I_r02 = [0.0031 0 0;0 0.0484 0;0 0 0.0484];
r30I_r03 = [0.0606 0 0;0 0.0053 0;0 0 0.0606];
r40I_r04 = [0.0022 0 0;0 0.0022 0;0 0 0.0014];
% ------------------------------------------------------------
% Vectores ri0pi, ri0si.
% ------------------------------------------------------------
r10p1 = ri0pi(a(1), d(1), alfa(1));
r20p2 = ri0pi(a(2), d(2), alfa(2));
r30p3 = ri0pi(a(3), d(3), alfa(3));
r40p4 = ri0pi(a(4), d(4), alfa(4));
r50p5 = zeros(3,1);
r10s1 = ri0si(a(1), d(1), alfa(1), factor1);
r20s2 = ri0si(a(2), d(2), alfa(2), factor2);
r30s3 = ri0si(a(3), d(3), alfa(3), factor3);
r40s4 = ri0si(a(4), d(4), alfa(4), factor4);
r50s5 = zeros(3,1);](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-60-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 3 .- Pág. 13
% ------------------------------------------------------------
% Matrices de transformacion
% ------------------------------------------------------------
r01 = dh(teta(1), alfa(1)); r10 = r01';
r12 = dh(teta(2), alfa(2)); r21 = r12';
r23 = dh(teta(3), alfa(3)); r32 = r23';
r34 = dh(teta(4), alfa(4)); r43 = r34';
r45 = eye(3); r54 = r45';
% ------------------------------------------------------------
% Velocidad angular de las articulaciones
% ------------------------------------------------------------
r00w0 = zeros(3,1);
r10w1 = ri0wi(r10, r00w0, qp(1));
r20w2 = r21*r10w1;
r30w3 = r32*r20w2;
r40w4 = ri0wi(r43, r30w3, qp(4));
r50w5 = ri0wi(r54, r40w4, 0);
% ------------------------------------------------------------
% Aceleracion angular de las articulaciones
% ------------------------------------------------------------
r00wp0 = zeros(3,1);
r10wp1 = ri0wpi(r10, r00wp0, r00w0, qp(1), qpp(1));
r20wp2 = r21*r10wp1;
r30wp3 = r32*r20wp2;
r40wp4 = ri0wpi(r43, r30wp3, r30w3, qp(4), qpp(4));
r50wp5 = ri0wpi(r54, r40wp4, r40w4, 0, 0);
% ------------------------------------------------------------
% Aceleracion lineal articular
% ------------------------------------------------------------
r00vp0 = [0; 0; g];
r10vp1 = ri0vpi_r(r10, r00vp0, r10wp1, r10w1, r10p1);
r20vp2 = ri0vpi_p(r21, r10vp1, r20wp2, r20w2, r20p2, qp(2), qpp(2));
r30vp3 = ri0vpi_p(r32, r20vp2, r30wp3, r30w3, r30p3, qp(3), qpp(3));
r40vp4 = ri0vpi_r(r43, r30vp3, r40wp4, r40w4, r40p4);
r50vp5 = ri0vpi_r(r54, r40vp4, r50wp5, r50w5, r50p5);
% ------------------------------------------------------------
% Aceleracion del centro de masa de cada elemento
% ------------------------------------------------------------
r10a1 = ri0ai(r10vp1, r10wp1, r10w1, r10s1);
r20a2 = ri0ai(r20vp2, r20wp2, r20w2, r20s2);
r30a3 = ri0ai(r30vp3, r30wp3, r30w3, r30s3);
r40a4 = ri0ai(r40vp4, r40wp4, r40w4, r40s4);
r50a5 = ri0ai(r50vp5, r50wp5, r50w5, r50s5);
% ------------------------------------------------------------
% Fuerza en el centro de masa de cada elemento
% ------------------------------------------------------------
r50f5 = ri0fi(r50a5, m5);
r40f4 = ri0fi(r40a4, m4);
r30f3 = ri0fi(r30a3, m3);
r20f2 = ri0fi(r20a2, m2);
r10f1 = ri0fi(r10a1, m1);
% ------------------------------------------------------------
% Par en el centro de masa de cada elemento
% ------------------------------------------------------------
r50n5 = ri0ni(r50wp5, r50w5, Iexter);](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-61-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 3 .- Pág. 14
r40n4 = ri0ni(r40wp4, r40w4, r40I_r04);
r30n3 = ri0ni(r30wp3, r30w3, r30I_r03);
r20n2 = ri0ni(r20wp2, r20w2, r20I_r02);
r10n1 = ri0ni(r10wp1, r10w1, r10I_r01);
% ------------------------------------------------------------
% Fuerzas articulares
% ------------------------------------------------------------
r50f5a = r50f5;
r40f4a = ri0fia(r45, r50f5a, r40f4);
r30f3a = ri0fia(r34, r40f4a, r30f3);
r20f2a = ri0fia(r23, r30f3a, r20f2);
r10f1a = ri0fia(r12, r20f2a, r10f1);
% ------------------------------------------------------------
% Pares articulares
% ------------------------------------------------------------
r20p1 = r21*(r10p1); r30p2 = r32*(r20p2);
r40p3 = r43*(r30p3); r50p4 = r54*(r40p4);
r50n5a = r50n5;
r40n4a = ri0nia(r45, r50n5a, r50f5a, r40n4, r40f4, r50p4, r40p4,
r40s4);
r30n3a = ri0nia(r34, r40n4a, r40f4a, r30n3, r30f3, r40p3, r30p3,
r30s3);
r20n2a = ri0nia(r23, r30n3a, r30f3a, r20n2, r20f2, r30p2, r20p2,
r20s2);
r10n1a = ri0nia(r12, r20n2a, r20f2a, r10n1, r10f1, r20p1, r10p1,
r10s1);
% ------------------------------------------------------------
% Fuerzas y pares de accionamientos
% ------------------------------------------------------------
t_1 = t_r(r10, r10n1a, qp(1), b1);
t_2 = f_p(r21, r20f2a, qp(2), b2);
t_3 = f_p(r32, r30f3a, qp(3), b3);
t_4 = t_r(r43, r40n4a, qp(4), b4);
tau = [t_1; t_2; t_3; t_4];
⇒ NOTA: Debe notarse que los parámetros físicos y geométricos del robot se han
introducido en el código. Se recuerda que los parámetros de D-H son característicos de
cada robot. El factor de posición del centro de masas de cada eslabón, su masa y su
inercia son datos del robot, así como los coeficientes de rozamiento viscoso aplicables
en cada articulación.
Se recomienda que compruebe la función para velocidades y aceleraciones nulas,
observando los resultados que se obtienen. En el ejemplo siguiente, se introducen
velocidades y aceleraciones nulas en todas las articulaciones. Se puede comprobar como
la fuerza en la articulación 2 (156 N) corresponde con el peso de los eslabones 2,3,4 y la
masa exterior que debe ser soportado por la articulación.](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-62-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 3 .- Pág. 15
» q=[0 0.5 0.4 0];
» qp=[0 0 0 0];
» qpp=qp;
» m4=3;
» iext=0.05*eye(3);
» tau=newtoneuler4(q,qp,qpp,9.8,m4,iext)
tau =
0.0000
156.8000
0.0000
0
»
Ejemplo 3.2
Se muestra a continuación la implementación del algoritmo de N-E para el robot
rotacional de 6 gdl.
Se observa que a diferencia del ejemplo
anterior, en este caso solamente se utilizan las
librerías de las funciones de enlaces
rotacionales.
Código en MatLab
. A continuación se presenta la función NEWTONEULER6,
utilizada para resolver la dinámica inversa del robot de 6 gdl. Realizando help
NEWTONEULER6, la función nos informa sobre los parámetros necesarios para
realizar los cálculos.
% NEWTONEULER6 Dinámica inversa utilizando el método de Newton-Euler.
% TAU = NEWTONEULER6(Q, QP, QPP, G, M7, IEXTER) calcula el vector
% 6x1 de pares/fuerzas de entrada a las articulaciones. Q el vector
% 6x1 de coordenadas articulares. QP es el vector 6x1 que representa
% la velocidad de cada articulación. QPP es el vector 6x1 que indica
% la aceleración de cada articulación. G es el valor de la gravedad (m/s^2).
% M7 es la masa de la carga externa(Kg) que transporta el brazo robot.
% IEXTER es la matriz 3x3 de inercia de la carga exterior(Kg-m^2).
%
% See also DH, RI0PI, RI0SI, RI0WI, RI0WIP, RI0VPI_R, RI0AI, RI0FI, RI0NI,
% RI0FIA, RI0NIA, T_R.
function tau = newtoneuler6(q,qp,qpp,g,m7,Iexter);
% ------------------------------------------------------------
% Parámetros Denavit-Hartenberg del robot
% ------------------------------------------------------------](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-63-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 3 .- Pág. 16
teta = q;
d = [0.315 0 0 0.5 0 0.08];
a = [0 0.45 0 0 0 0 ];
alfa = [-pi/2 0 pi/2 -pi/2 pi/2 0 ];
% ------------------------------------------------------------
% Factores de posicionamiento de los centros de gravedad
% ------------------------------------------------------------
factor1 = -0.5; factor2 = -0.5; factor3 = -0.5;
factor4 = -0.5; factor5 = -0.5; factor6 = -0.5;
% ------------------------------------------------------------
% Masa de cada elemento (Kg)
% ------------------------------------------------------------
m1 = 2.78; m2 = 10.25; m3 = 0;
m4 = 5.57; m5 = 0; m6 = 1.98;
% ------------------------------------------------------------
% Coeficiente de rozamiento viscoso de cada articulacion
% ------------------------------------------------------------
b1 = 0.05; b2 = 0.05; b3 = 0.05;
b4 = 0.05; b5 = 0.05; b6= 0.05;
% ------------------------------------------------------------
% Matrices de Inercia (Kg-m^2)
% ------------------------------------------------------------
r10I_r01 = [0.0191 0 0;0 0.0191 0;0 0 0.0068];
r20I_r02 = [0.0031 0 0;0 0.0484 0;0 0 0.0484];
r30I_r03 = zeros(3,3);
r40I_r04 = [0.0606 0 0;0 0.0053 0;0 0 0.0606];
r50I_r05 = zeros(3,3);
r60I_r06 = [0.0022 0 0;0 0.0022 0;0 0 0.0014];
% ------------------------------------------------------------
% Vectores ri0pi, ri0si.
% ------------------------------------------------------------
r10p1 = ri0pi(a(1), d(1), alfa(1));
r20p2 = ri0pi(a(2), d(2), alfa(2));
r30p3 = ri0pi(a(3), d(3), alfa(3));
r40p4 = ri0pi(a(4), d(4), alfa(4));
r50p5 = ri0pi(a(5), d(5), alfa(5));
r60p6 = ri0pi(a(6), d(6), alfa(6));
r70p7 = zeros(3,1);
r10s1 = ri0si(a(1), d(1), alfa(1), factor1);
r20s2 = ri0si(a(2), d(2), alfa(2), factor2);
r30s3 = ri0si(a(3), d(3), alfa(3), factor3);
r40s4 = ri0si(a(4), d(4), alfa(4), factor4);
r50s5 = ri0si(a(5), d(5), alfa(5), factor5);
r60s6 = ri0si(a(6), d(6), alfa(6), factor6);
r70s7 = zeros(3,1);
% ------------------------------------------------------------
% Matrices de transformacion
% ------------------------------------------------------------
r01 = dh(teta(1), alfa(1)); r10 = r01';
r12 = dh(teta(2), alfa(2)); r21 = r12';
r23 = dh(teta(3), alfa(3)); r32 = r23';
r34 = dh(teta(4), alfa(4)); r43 = r34';
r45 = dh(teta(5), alfa(5)); r54 = r45';
r56 = dh(teta(6), alfa(6)); r65 = r56';
r67 = eye(3); r76 = r67';](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-64-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 3 .- Pág. 17
% ------------------------------------------------------------
% Velocidad angular de las articulaciones
% ------------------------------------------------------------
r00w0 = zeros(3,1);
r10w1 = ri0wi(r10, r00w0, qp(1));
r20w2 = ri0wi(r21, r10w1, qp(2));
r30w3 = ri0wi(r32, r20w2, qp(3));
r40w4 = ri0wi(r43, r30w3, qp(4));
r50w5 = ri0wi(r54, r40w4, qp(5));
r60w6 = ri0wi(r65, r50w5, qp(6));
r70w7 = ri0wi(r76, r60w6, 0);
% ------------------------------------------------------------
% Aceleracion angular de las articulaciones
% ------------------------------------------------------------
r00wp0 = zeros(3,1);
r10wp1 = ri0wpi(r10, r00wp0, r00w0, qp(1), qpp(1));
r20wp2 = ri0wpi(r21, r10wp1, r10w1, qp(2), qpp(2));
r30wp3 = ri0wpi(r32, r20wp2, r20w2, qp(3), qpp(3));
r40wp4 = ri0wpi(r43, r30wp3, r30w3, qp(4), qpp(4));
r50wp5 = ri0wpi(r54, r40wp4, r40w4, qp(5), qpp(5));
r60wp6 = ri0wpi(r65, r50wp5, r50w5, qp(6), qpp(6));
r70wp7 = ri0wpi(r76, r60wp6, r60w6, 0, 0);
% ------------------------------------------------------------
% Aceleracion lineal articular
% ------------------------------------------------------------
r00vp0 = [0; 0; g];
r10vp1 = ri0vpi_r(r10, r00vp0, r10wp1, r10w1, r10p1);
r20vp2 = ri0vpi_r(r21, r10vp1, r20wp2, r20w2, r20p2);
r30vp3 = ri0vpi_r(r32, r20vp2, r30wp3, r30w3, r30p3);
r40vp4 = ri0vpi_r(r43, r30vp3, r40wp4, r40w4, r40p4);
r50vp5 = ri0vpi_r(r54, r40vp4, r50wp5, r50w5, r50p5);
r60vp6 = ri0vpi_r(r65, r50vp5, r60wp6, r60w6, r60p6);
r70vp7 = ri0vpi_r(r76, r60vp6, r70wp7, r70w7, r70p7);
% ------------------------------------------------------------
% Aceleracion del centro de masa de cada elemento
% ------------------------------------------------------------
r10a1 = ri0ai(r10vp1, r10wp1, r10w1, r10s1);
r20a2 = ri0ai(r20vp2, r20wp2, r20w2, r20s2);
r30a3 = ri0ai(r30vp3, r30wp3, r30w3, r30s3);
r40a4 = ri0ai(r40vp4, r40wp4, r40w4, r40s4);
r50a5 = ri0ai(r50vp5, r50wp5, r50w5, r50s5);
r60a6 = ri0ai(r60vp6, r60wp6, r60w6, r60s6);
r70a7 = ri0ai(r70vp7, r70wp7, r70w7, r70s7);
% ------------------------------------------------------------
% Fuerza en el centro de masa de cada elemento
% ------------------------------------------------------------
r70f7 = ri0fi(r70a7, m7);
r60f6 = ri0fi(r60a6, m6);
r50f5 = ri0fi(r50a5, m5);
r40f4 = ri0fi(r40a4, m4);
r30f3 = ri0fi(r30a3, m3);
r20f2 = ri0fi(r20a2, m2);
r10f1 = ri0fi(r10a1, m1);
% ------------------------------------------------------------
% Par en el centro de masa de cada elemento
% ------------------------------------------------------------](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-65-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 3 .- Pág. 18
r70n7 = ri0ni(r70wp7, r70w7, Iexter);
r60n6 = ri0ni(r60wp6, r60w6, r60I_r06);
r50n5 = ri0ni(r50wp5, r50w5, r50I_r05);
r40n4 = ri0ni(r40wp4, r40w4, r40I_r04);
r30n3 = ri0ni(r30wp3, r30w3, r30I_r03);
r20n2 = ri0ni(r20wp2, r20w2, r20I_r02);
r10n1 = ri0ni(r10wp1, r10w1, r10I_r01);
% ------------------------------------------------------------
% Fuerzas articulares
% ------------------------------------------------------------
r70f7a = r70f7;
r60f6a = ri0fia(r67, r70f7a, r60f6);
r50f5a = ri0fia(r56, r60f6a, r50f5);
r40f4a = ri0fia(r45, r50f5a, r40f4);
r30f3a = ri0fia(r34, r40f4a, r30f3);
r20f2a = ri0fia(r23, r30f3a, r20f2);
r10f1a = ri0fia(r12, r20f2a, r10f1);
% ------------------------------------------------------------
% Pares articulares
% ------------------------------------------------------------
r20p1 = r21*(r10p1); r30p2 = r32*(r20p2);
r40p3 = r43*(r30p3); r50p4 = r54*(r40p4);
r60p5 = r65*(r50p5); r70p6 = r76*(r60p6);
r70n7a = r70n7;
r60n6a = ri0nia(r67, r70n7a, r70f7a, r60n6, r60f6, r70p6, r60p6,
r60s6);
r50n5a = ri0nia(r56, r60n6a, r60f6a, r50n5, r50f5, r60p5, r50p5,
r50s5);
r40n4a = ri0nia(r45, r50n5a, r50f5a, r40n4, r40f4, r50p4, r40p4,
r40s4);
r30n3a = ri0nia(r34, r40n4a, r40f4a, r30n3, r30f3, r40p3, r30p3,
r30s3);
r20n2a = ri0nia(r23, r30n3a, r30f3a, r20n2, r20f2, r30p2, r20p2,
r20s2);
r10n1a = ri0nia(r12, r20n2a, r20f2a, r10n1, r10f1, r20p1, r10p1,
r10s1);
% ------------------------------------------------------------
% Fuerzas y pares de accionamientos
% ------------------------------------------------------------
t_1 = t_r(r10, r10n1a, qp(1), b1);
t_2 = t_r(r21, r20n2a, qp(2), b2);
t_3 = t_r(r32, r30n3a, qp(3), b3);
t_4 = t_r(r43, r40n4a, qp(4), b4);
t_5 = t_r(r54, r50n5a, qp(5), b5);
t_6 = t_r(r65, r60n6a, qp(6), b6);
tau = [t_1; t_2; t_3; t_4; t_5; t_6];
⇒ NOTA: Debe notarse que los parámetros físicos y geométricos del robot se han
introducido en el código. Se recuerda que los parámetros de D-H son característicos de
cada robot. El factor de posición del centro de masas de cada eslabón, su masa y su
inercia son datos del robot, así como los coeficientes de rozamiento viscoso aplicables
en cada articulación.](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-66-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 3 .- Pág. 19
3.3.-Dinámica directa. Método de Walker-Orin.
Las ecuaciones de movimiento planteadas en el apartado anterior permiten
resolver el problema de la dinámica directa.
M.W.Walker y D.E.Orin [3 ] presentaron en 1982 cuatro métodos para la resolución del
problema dinámico directo de una cadena cinemática abierta utilizando la formulación
de N-E. En el artículo se realiza una comparación de la eficiencia computacional de los
cuatro métodos presentados, concluyendo que el tercero de los presentados es el más
eficiente frente al tiempo de cómputo. Para la realización de esta práctica los autores
han implementado el tercer método de Walker-Orin. (los ficheros se proporcionan
durante la práctica).
⇒ NOTA: Se recomienda al lector interesado la lectura del artículo de M.W.Walker y
D.E.Orin, dónde se presentan el resto de métodos que no han sido usados en este libro.
Walker y Orin resuelven la ecuación general del robot:
τ=+++ kqKqGqqqCqqH T
)()(),()( (3.34)
donde:
)(qH Matriz no singular NxN de los momentos de inercia.
),( qqC Matriz NxN que contabiliza los efectos de las aceleraciones centrífugas y
de Coriolis.
)(qG Vector Nx1 que contabiliza los efectos de la gravedad.
)(qK Matriz Jacobiana 6xN que especifica los pares (fuerzas) creados en cada
articulación debido a las fuerzas y momentos externos aplicados sobre el
elemento N.
k Vector 6x1 de los momentos y fuerzas externas ejercidos sobre el
elemento N.
τ Vector Nx1 de los pares (fuerzas) de cada articulación. (tau en los
ejemplos anteriores).
q Vector Nx1 de las variables articulares.
De la ecuación (3.34) se observa que las fuerzas y pares en las articulaciones son
funciones lineales de las aceleraciones articulares. Se define b como un vector
equivalente a los efectos de la gravedad, las aceleraciones centrifugas y de Coriolis y las
fuerzas externas aplicadas sobre el elemento N:
kqKqGqqqCb T
)()(),( ++= (3.35)
Entonces, la ecuación (3.34) se puede poner como:
)()( bqqH −= τ (3.36)](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-67-320.jpg)

![Prácticas de Robótica utilizando Matlab®
Práctica 3 .- Pág. 21
luego empezando con i=j , las ecuaciones anteriores pueden ser usadas para obtener ni y
fi para i≤ j.
Los componentes de la matriz de momentos de inercia a lo largo de la columna j son
iguales a los pares y fuerzas generados en las articulaciones. Luego para i≤ j:
ii nz 1− para articulación i rotacional
ijH (3.40)
ii fz 1− para articulación j traslacional
Los parámetros Mj,cj yEj utilizados en las ecuaciones (3.37) y (3.38) se calculan con las
siguientes ecuaciones:
para el elemento N:
NN mM =
*
NNN psc +=
NN JE =
y para el resto:
jjj mMM += +1
( ) ( )[ ]*
11
*1
jjjjjj
j
j pcMpsm
M
c +++= ++
( ) ( ) ( )( )[ ]
( ) ( ) ( )( )[ ]T
jjjjjjjjjjjjjj
T
jjjjjjjjjjjjjjj
cpccpsIcpscpsmJ
cpccpcIcpccpcMEE
−+−+−−+−+++
+−+−+−−+−++=
+
++++−−
*
1
***
*
1
*
1
*
1
*
111
*
*
donde:
mj masa del elemento j
sj posición del centro de masas del elemento i respecto a las coordenadas del
elemento j
Jj matriz de momentos de inercia del elemento j
I matriz identidad 3x3](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-69-320.jpg)




![Prácticas de Robótica utilizando Matlab®
Práctica 3 .- Pág. 26
% Vector de tiempo dividido en intervalos
t = 0:pint:tsim;
% Número de intervalos + 1
n = length(t);
% Inicialización de la matriz de coordenadas articulares
mat_q(:,1) = q;
% Se calcula las coordenadas articulares del robot
% en cada intervalo de la simulación
for i=2:n
% Se calcula la posición y la velocidad de cada articulación
% combinando el tercer método de Walker & Orin con el método
% de integración de Runge-Kutta.
[q qp] = walkerorinrunge3(q,qp,zeros(3,1),t(i-1),t(i),masaext,inerciaext);
% Se almacenan las coordenadas articulares
mat_q(:,i) = q;
end
Hay que destacar que para actualizar la posición y la velocidad de cada articulación se
utiliza el método de Walker y Orin en combinación con el método de integración de
Runge-Kutta de orden cuatro. Esto se debe a que el tercer método de Walker y Orin
proporciona la aceleración de cada articulación, por lo que es necesario utilizar un
método de integración para obtener la posición y la velocidad de cada articulación. A
continuación se muestra el código en Matlab
de la función WALKERORINRUNGE3,
que combina el método de Walker y Orin junto con el de Runge-Kutta para el cálculo de
la posición y velocidad de cada articulación:
% WALKERORINRUNGE3 Tercer método de Walker & Orin.
% [QFIN, QPFIN] = WALKERORINRUNGE3(QINI, QPINI, PAR, T0, TF, MASAEXT,
% INERCIAEXT) calcula la posición y la velocidad de cada articulación
% del péndulo de 3 GDL combinando el tercer método de Walker & Orin
% con el método de integración de Runge-Kutta de orden cuatro.
% QINI es el vector 3x1 de variables articulares en el instante de
% tiempo T0. QPINI es el vector 3x1 que representa la velocidad de
% cada articulación en el instante de tiempo T0. PAR es el vector
% 3x1 que representa el par de entrada a cada articulación. T0 y TF
% representan, respectivamente, los valores de inicio y de fin del
% intervalo de tiempo. MASAEXT es la masa de la carga externa.
% INERCIAEXT es la inercia de la carga externa. En QFIN y QPFIN se
% devuelven, respectivamente, los vectores 3x1 de posición y
% velocidad de cada articulación en el instante de tiempo TF.
%
% See also WALKERORIN3.
function [qfin, qpfin] =
walkerorinrunge3(qini,qpini,par,t0,tf,masaext,inerciaext);
h = (tf-t0);
% Primer termino.
t1 = t0;
q1 = qini;
qp1= qpini;
v1 = h*qpini;
w1 = h*walkerorin3(q1,qp1,par,masaext,inerciaext);
% Segundo termino.
t2 = t0 + .5*h;
q2 = qini + .5*v1;
qp2= qpini + .5*w1;](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-74-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 3 .- Pág. 27
v2 = h*(qpini + .5*w1);
w2 = h*walkerorin3(q2,qp2,par,masaext,inerciaext);
% Tercer termino.
t3 = t0 + .5*h;
q3 = qini + .5*v2;
qp3= qpini + .5*w2;
v3 = h*(qpini + .5*w2);
w3 = h*walkerorin3(q3,qp3,par,masaext,inerciaext);
% Cuarto termino.
t4 = t0 + h;
q4 = qini + v3;
qp4= qpini + w3;
v4 = h*(qpini + w3);
w4 = h*walkerorin3(q4,qp4,par,masaext,inerciaext);
% Formula de Runge-Kutta.
qfin = qini + (v1 + 2*v2 + 2*v3 + v4)/6;
qpfin = qpini + (w1 + 2*w2 + 2*w3 + w4)/6;
% Redondeo para evitar oscilacion numerica.
qfin = round(qfin*1e13)/1e13;
qpfin = round(qpfin*1e13)/1e13;
En el código anterior se hacen varias llamadas a la función WALKERORIN3. Esta
función calcula la dinámica directa del péndulo de 3GDL utilizando el tercer método de
Walker y Orin. Para el cálculo de la dinámica directa se utilizan las funciones
NEWTONEULER3 y H3.
Para simular el comportamiento del péndulo de 3GDL durante 1 segundo considerando
un periodo de integración de 0.001 segundos se procedería de la siguiente manera en
Matlab
:
» mat_q=simula3(1,0.001);
»
Para comprobar visualmente el comportamiento del péndulo de 3GDL se ha
desarrollado la función ANIMACION3. El código de esta función se muestra a
continuación:
% ANIMACION3 Animación del movimiento del péndulo de 3GDL.
% ANIMACION3(MAT_Q) realiza la animación del movimiento del
% péndulo de 3GDL a partir de las coordenadas articulares
% almacenadas en la matriz MAT_Q. MAT_Q contiene 3 filas
% y una columna para cada disposición del robot durante el
% movimiento.
function animacion3(mat_q)
% Parámetros Denavit-Hartenberg del robot
d = [0 0 0];
a = [1 1 1];
alfa = [0 0 0];
% Vector de posicion (x, y) del sistema de coordenadas de referencia
x0 = 0; y0 = 0;](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-75-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 3 .- Pág. 28
% Se dibuja el sistema de coordenadas de referencia. Se asigna el modo XOR
para borrar
% sólo el robot dibujado anteriormente.
p = plot(x0,y0,'EraseMode','xor');
% Se asigna una rejilla a los ejes
grid;
% Se establecen los límites de los ejes
axis([-3.2 3.2 -3.1 1]);
% Mantiene el gráfico actual
hold on;
% Número de columnas de la matriz
n = size(mat_q,2);
% Se dibuja la disposición del robot correspondiente a cada columna
for i=1:n
% Variables articulares del brazo robot
teta1 = mat_q(1,i);
teta2 = mat_q(2,i);
teta3 = mat_q(3,i);
% Matrices de transformación homogénea entre sistemas de coordenadas
consecutivos
A01 = denavit(teta1, d(1), a(1), alfa(1));
A12 = denavit(teta2, d(2), a(2), alfa(2));
A23 = denavit(teta3, d(3), a(3), alfa(3));
% Matrices de transformación del primer sistema al correspondiente
A02 = A01 * A12;
A03 = A02 * A23;
% Vector de posicion (x, y) de cada sistema de coordenadas
x1 = A01(1,4); y1 = A01(2,4);
x2 = A02(1,4); y2 = A02(2,4);
x3 = A03(1,4); y3 = A03(2,4);
% Se dibuja el robot
x = [x0 x1 x2 x3];
y = [y0 y1 y2 y3];
set(p,'XData',x,'YData',y);
% Se fuerza a MATLAB a actualizar la pantalla
drawnow;
end
Para realizar la animación del comportamiento simulado anteriormente se procedería de
la siguiente manera en Matlab:
» animacion3(mat_q)
»
Al ejecutar la función en Matlab
nos aparecerá una ventana similar a mostrada en la
figura 3.5 en la que se visualizará la animación.](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-76-320.jpg)




![Prácticas de Robótica utilizando Matlab®
Práctica 4 .- Pág. 5
El subsistema mostrado en la figura 4.3 hace uso de una función desarrollada en Matlab
trapezoidal.m. Esta función sirve para generar la velocidad y aceleración de la
articulación en cada instante de tiempo según los parámetros elegidos del perfil de
velocidad, que recordemos que son la velocidad máxima, el tiempo de aceleración, el
tiempo constante y el tiempo de deceleración. El código fuente de esta función se
muestra a continuación:
% TRAPEZOIDAL Perfil de velocidad trapezoidal
% PERFIL=TRAPEZOIDAL(U) devuelve un vector 1x2 que contiene la velocidad
% y la aceleración de un perfil de velocidad trapezoidal en un determinado
% instante de tiempo. PERFIL(1) contiene la velocidad y PERFIL(2) la
% aceleración. U(1) representa el instante de tiempo actual(seg). U(2) es
% la velocidad máxima. U(3) es el tiempo de aceleración(seg). U(4) es el
% tiempo de velocidad constante(seg). U(5) es el tiempo de
deceleración(seg).
function perfil=trapezoidal(u)
t = u(1); % Instante de tiempo actual
velmax = u(2); % Velocidad máxima
tacel = u(3); % Tiempo de aceleración
tconst = u(4); % Tiempo de velocidad constante
tdecel = u(5); % Tiempo de deceleración
% Se calcula la velocidad y la aceleración
if t <= tacel
% Intervalo de aceleración
acel = velmax/tacel;
vel = acel*t;
else
if t < (tacel+tconst)
% Intervalo de velocidad constante
vel = velmax;
acel = 0;
else
if t>(tacel+tconst+tdecel)
% Velocidad y aceleración nula
vel = 0;
acel = 0;
else
% Intervalo de deceleración
acel = -velmax/tdecel;
vel = velmax+acel*(t-tacel-tconst);
end
end
end
% Se devuelve la velocidad y la aceleración
perfil = [vel acel];
Para obtener el par o fuerza de cada articulación se ha desarrollado en Matlab
la
función dininv4gdl.m; que calcula el par o fuerza de cada articulación cuando el robot
transporta una determinada carga en función de la posición, velocidad y aceleración de
cada articulación. Esta función hace uso de la función newtoneuler4.m, explicada en la
práctica 3. El código fuente de dininv4gdl.m se muestra a continuación:](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-82-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 4 .- Pág. 6
Una vez presentada la herramienta, así como los ficheros que se van a utilizar para
calcular los pares y fuerzas pico y nominal de cada articulación, se va a proceder a
obtener estos pares y fuerzas en el caso del robot de 4 GDL.
En primer lugar hay que destacar que la peor posición en la que se puede encontrar el
robot se produce cuando las dos articulaciones prismáticas han alcanzado su valor
máximo. Se considerará que el valor máximo de la segunda articulación (q2) es de 1m,
mientras que el de la tercera (q3) es de 1.2m. El valor de la primera y cuarta articulación
no influye en el cálculo de los pares/fuerzas máximas. Por lo tanto, por comodidad, la
peor posición del robot vendrá dada por:
( )02.110=q
Para ver la configuración del robot en la peor posición podemos utilizar la función
drawrobot3d4 que vimos en la práctica 2:
» drawrobot3d4([0 1 1.2 0]')
La ejecución de la función anterior muestra, efectivamente, que el vector de
coordenadas articulares anterior corresponde a la peor disposición del robot, como se
puede apreciar en la figura 4.4.
% DININV4GDL Dinámica inversa de un robot de 4GDL.
% PAR = DININV4GDL(ENTRADA) calcula el vector 4x1 de pares/fuerzas de
% entrada a las articulaciones utilizando el método de Newton-Euler.
% ENTRADA(1:4) representa la posición de cada articulación.
% ENTRADA(5:8) es la velocidad de cada articulación. ENTRADA(9:12)
% es la aceleración de cada articulación.
%
% See also NEWTONEULER4.
function par = dininv4gld(entrada)
q = entrada(1:4); % Posición de cada articulación
qp = entrada(5:8); % Velocidad de cada articulación
qpp = entrada(9:12); % Aceleración de cada articulación
% Parámetros de la carga
masaext = 10;
inerciaext = [0.0167 0 0;0 0.0167 0;0 0 0.0167];
% Se calcula el vector de pares/fuerzas utilizando Newton-Euler
par = newtoneuler4(q,qp,qpp,9.8,masaext,inerciaext);](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-83-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 4 .- Pág. 7
Figura 4.4. Peor disposición del robot. Se obtiene al ejecutar drawrobot3d4([0 1 1.2 0]').
Como ya se ha comentado anteriormente, los parámetros que caracterizan a un perfil de
velocidad trapezoidal son:
- Velocidad máxima
- Tiempo de aceleración
- Tiempo constante
- Tiempo de deceleración
Para el caso del robot de 4 GDL se va a suponer que la velocidad máxima para las
articulaciones rotacionales es de π/3 rad/s, mientras que en el caso de las prismáticas es
de 1 m/s. Se va a considerar que el tiempo de aceleración es 0.1 segundos, lo que quiere
decir que se dispone de 0.1 segundos para alcanzar la velocidad máxima. Como tiempo
constante se va a tomar 0.4 segundos y como tiempo de deceleración 0.1 segundos. Es
importante destacar que en función de la articulación se considerará la velocidad
máxima positiva o negativa. En el caso de las articulaciones 1 y 4 es independiente
considerar la velocidad máxima positiva o negativa, ya que a efectos de requerimientos
de par, no hay diferencia en girar la articulación en un sentido o en otro. Para la
obtención de los pares pico y nominal se ha considerado la velocidad máxima positiva.
En las articulaciones 2 y 3 los mayores requerimientos de par se producirán cuando la
articulación se desplace en el sentido positivo del eje z. Por lo tanto, para ambas
articulaciones se ha considerado la velocidad máxima positiva. Ver figura 4.5.](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-84-320.jpg)

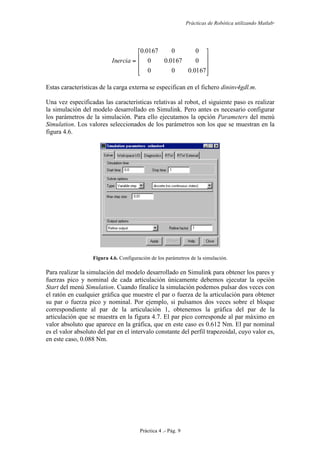

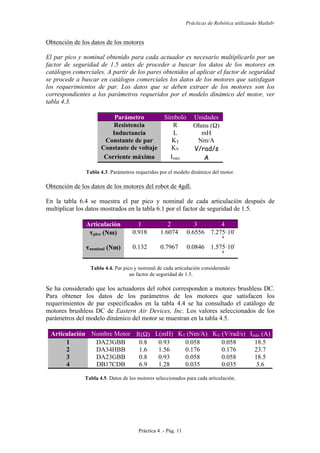


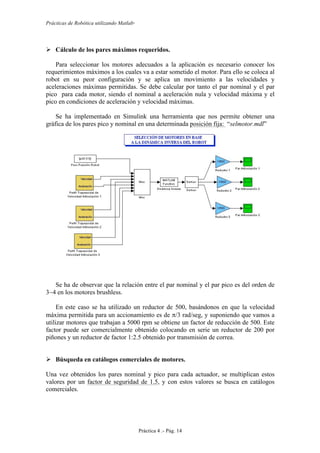






![Prácticas de Robótica utilizando Matlab®
Práctica 5 .- Pág. 6
5.4.1.- Trayectorias de articulación interpolada
Con el objetivo de que el movimiento del robot sea suave y esté de acuerdo con
las restricciones de los actuadores se divide cada trayectoria articular en tres segmentos,
correspondientes a la aceleración del motor, el periodo de velocidad máxima y la
deceleración o frenado del motor. La gráfica siguiente muestra esta división en la que se
puede observar como los periodos de aceleración y frenado ofrecen un movimiento
suave del robot.
Las restricciones en los puntos de control que se utilizan para resolver el cálculo de los
polinomios interpoladores son las siguientes:
⇒ Posición inicial (t0)
Posición θ(t0)
Velocidad inicial (normalmente nula)
Aceleración inicial (normalmente nula)
⇒ Posición intermedia (t1)
Posición θ(t1)
Continuidad en posición
Continuidad en velocidad
Continuidad en aceleración
⇒ Posición intermedia (t2)
Posición θ(t2)
Continuidad en posición
Continuidad en velocidad
Continuidad en aceleración
⇒ Posición final (t3)
Posición θ(t3)
Velocidad final (normalmente nula)
Aceleración final (normalmente nula)
Se pueden encontrar en la literatura específica muchos polinomios que permiten
cumplir con las anteriores restricciones. Una de estas soluciones es la combinación 4-3-
4 [1] que se explica brevemente a continuación.
Articulación i
Tiempo
Posición
t0 t1 t2 t3
θ(t0)
θ(t1)
θ(t2)
θ(t3) Aceleración
Vel.Máx.
Frenado](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-98-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 5 .- Pág. 7
5.4.2.- Polinomios 4-3-4
Utilizando este tipo de polinomios interpoladores se tiene los siguientes tres
segmentos de trayectorias para cada articulación:
• 1er
segmento de trayectoria. Es un polinomio de cuarto grado que especifica el
intervalo de aceleración del motor.
1011
2
12
3
13
4
141 )( atatatatath ++++= (5.2)
• 2º segmento de trayectoria. Es un polinomio de tercer grado que especifica la
trayectoria desde la primera posición intermedia (t1) hasta la posición t2.
2021
2
22
3
232 )( atatatath +++= (5.3)
• 3er
segmento de trayectoria. Es un polinomio de cuarto grado que especifica la
trayectoria durante el período final de frenado del motor.
3031
2
32
3
33
4
343 )( atatatatath ++++= (5.4)
En primer lugar hay que considerar que al estar hallando las trayectorias
articulares para las N articulaciones del manipulador, es conveniente introducir una
variable de tiempo normalizada t∈[0,1], que permita simplificar los cálculos al evitar
tener que contabilizar los desfases temporales, de tal manera que t=0 corresponda al
inicio de cualquiera de los tres segmentos en que se ha dividido el camino y t=1
corresponda al final del segmento de trayectoria.
Matemáticamente, este cambio de variable queda expresado como:
1
1
−
−
−
−
=
i
i
i
t
ττ
ττ
(5.5)
Donde:
t variable de tiempo normalizado, t∈[0,1]
τ tiempo real en segundos
τi tiempo real la final del segmento de trayectoria i-ésimo
Las siguientes expresiones permiten obtener las relaciones necesarias para el
cálculo de los coeficientes de los tres polinomios buscados. Estas expresiones se
obtienen aplicando la regla de la cadena con el cambio de variable temporal descrito
anteriormente:
)(
1
th
t
v i
i
i
= (5.6)
)(
1
2
th
t
a i
i
i
= (5.7)](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-99-320.jpg)

![Prácticas de Robótica utilizando Matlab®
Práctica 5 .- Pág. 9
1
1
2
2 )1()0(
t
h
t
h
= y 2
1
1
2
2
2 )1()0(
t
h
t
h
= (5.21)
de donde se obtienen las igualdades siguientes:
0
34
1
10
1
2
10
1
13
1
14
2
21
=++++
−
t
tv
t
ta
t
a
t
a
t
a
(5.22)
0
6122
2
1
2
10
2
1
13
2
1
14
2
2
22
=+++
−
t
ta
t
a
t
a
t
a
(5.23)
Tercer segmento de trayectoria. Frenado
Para aplicar más cómodamente las condiciones de contorno conviene realizar un cambio
de variable, sustituyendo 1−= tt por t en la ecuación (5.4), de tal manera que 0=t
corresponde al instante final del segmento y 1−=t al instante inicial. La ecuación que
gobierna este segmento pasa a formularse como:
3031
2
32
3
33
4
343 )( atatatatath ++++= con [ ]0,1−∈t (5.24)
Aplicando las condiciones para 0=t y 1−=t
fha θ== )0(330 (5.25)
3
31
3
3 )0(
t
a
t
h
vf ==
(5.26)
2
3
32
2
3
3 2)0(
t
a
t
h
af ==
(5.27)
3
2
33334
3
3
34)1(
t
tvtaaa
t
h nff +−+−
=
−
(5.28)
2
3
2
33334
2
3
3
612)1(
t
taaa
t
h f+−
=
−
(5.29)
y aplicando continuidad:
3
3
2
2 )1()1(
t
h
t
h −
=
y 2
3
3
2
2
2 )1()1(
t
h
t
h −
=
(5.30)
0
2334
2
21
2
22
2
23
3
3
2
33332
=+++
−+−
t
a
t
a
t
a
t
tvtaaa ff
(5.31)
0
66612
2
2
22
2
2
23
2
3
2
33334
=++
−+−
t
a
t
a
t
taaa f
(5.32)](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-101-320.jpg)

![Prácticas de Robótica utilizando Matlab®
Práctica 5 .- Pág. 11
recalculan estas velocidades máximas admisibles que proporcionan un movimiento
coordinado. La función SINCRONIZADOR se muestra a continuación:
% SINCRONIZADOR Funcion que sincroniza los movimientos teniendo en
consideración
% las condiciones iniciales, finales, características de las articulaciones y
% velocidades nominales.
% [VELO2,TMAXIMO]=SINCRONIZADOR(Q0,QF,VELO) devuelve la nueva velocidad
% máxima de cada
% motor.
% Q0 posición inicial (coordenadas articulares).
% QF posición final (coordenadas articulares).
% VELO velocidad máxima nominal de cada actuador.
%
% Ver también PLANIFICADOR, CALCULOCOEF, SINCRONIZADOR, EVALPOS, EVALACEL.
function [velo2,tmaximo]=sincronizador(q0,qf,velo)
%--Calculo de tiempos aproximados.
taprox = abs((qf(:,1)-q0(:,1)))./velo;
tmaximo = max(taprox);
%--Nueva velocidad maxima de cada motor.
velo2=(qf(:,1)-q0(:,1))/tmaximo;
return
En la función CALCULOCOEF que se muestra a continuación se han
contemplado los casos en que un motor no necesite alcanzar su velocidad máxima
durante la trayectoria, debido a que el recorrido que debe efectuar es pequeño (o incluso
nulo). En estos casos el perfil de velocidades no tendrá la típica forma de trapecio, dado
que los tres segmentos de trayectoria se reducirán a dos.
% CALCULOCOEF Función de cálculo de los coeficientes de los polinomios 4-3-4.
%
% [CASO, A ,TT]=CALCULOCOEF(ELEM,VEL,Q0,QF,TMOTOR) calcula los
coeficientes
% de los polinomios interpolados 4-3-4 en base a las especificaciones de
% los actuadores y los puntos de inicio y final.
% La matriz A de 5x3 contiene los coeficientes de los polinomios interpolados.
% TT es el vector 3x1 de los intervalos de tiempo de aceleración, velocidad
% maxima y deceleración de los motores.
% caso=1: Cada motor logra alcanzar su velocidad maxima.
% caso=2: No hay tiempo de alcanzar la velocidad maxima de cada motor.
%
% Ver también PLANIFICADOR, SINCRONIZADOR, EVALPOS, EVALVEL, EVALACEL.
function [caso,A,tt] = calculocoef(elem,vel,q0,qf,tmotor)
%---------------------------------------------------------------------
%Tiempos de respuesta del motor (aceleración y frenado)
%---------------------------------------------------------------------
ti = tmotor(elem,1);
tf = tmotor(elem,2);
%---------------------------------------------------------------------
%Cálculo de los coeficientes.
%---------------------------------------------------------------------](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-103-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 5 .- Pág. 12
if vel(elem) ~= 0
%-Determinacion del caso
desp = (qf(elem,1) - q0(elem,1));
ttot = abs(desp/vel(elem));
if ttot > (ti + tf)
caso = 1;
else
caso = 2;
end;
%****************************** CASO 1********************************
if caso == 1
%vector de tiempo: Arranque - Velocidad Max - Desaceleracion
tt = [ ti ttot-(ti+tf) tf ];
%Determinacion de los coeficientes polinomiales
A = zeros(3,5);
%Coeficientes del polinomio de posicion
A(1,1) = q0(elem,1);
A(1,2) = q0(elem,2)*tt(1);
A(1,3) = q0(elem,3)*tt(1)^2/2;
A(1,4) = tt(1)*vel(elem) - A(1,2) - 4*A(1,3)/3;
A(1,5) = -tt(1)*vel(elem)/2 + A(1,2)/2 + A(1,3)/2;
%Coeficientes del polinomio de aceleracion
A(3,1) = qf(elem,1);
A(3,2) = qf(elem,2)*tt(3);
A(3,3) = qf(elem,3)*tt(3)^2/2;
A(3,4) = tt(3)*vel(elem) - A(3,2) + 4*A(3,3)/3;
A(3,5) = (tt(3)*vel(elem) - A(3,2) + A(3,3))/2;
%Espacio recorrido en los anteriores intervalos
x1 = A(1,2) + A(1,3) + A(1,4) + A(1,5);
x3 = A(3,2) - A(3,3) + A(3,4) - A(3,5);
x2 = qf(elem,1) - q0(elem,1) - ( x1 + x3);
%Tiempo real a velocidad maxima.
tt(2) = x2/vel(elem);
%Coeficientes del polinomio de velocidad.
A(2,1) = A(1,1) + A(1,2) + A(1,3) + A(1,4) + A(1,5);
A(2,2) = vel(elem)*tt(2);
%******************************** CASO 2******************************
elseif caso == 2
t = (ti + tf)/2;
tt = [ t t ];
A = zeros(2,5);
% Arranque del motor.
A(1,1) = q0(elem,1);
A(1,2) = q0(elem,2)*tt(1);
A(1,3) = q0(elem,3)*tt(1)^2/2;
% Desaceleracion del motor.
A(2,1) = qf(elem,1);](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-104-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 5 .- Pág. 13
A(2,2) = qf(elem,2)*tt(2);
A(2,3) = qf(elem,3)*tt(2)^2/2;
% Los polinomios para este caso son de quinto orden.
B = [ 1 1 1 -1;
6/tt(1)^2 12/tt(1)^2 0 0;
3/tt(1) 4/tt(1) -3/tt(2) 4/tt(2);
0 0 -6/tt(2)^2 12/tt(2)^2 ];
b = [ -A(1,1) + A(1,2) + A(1,3) + A(2,1) - A(2,2) + A(2,3);
-2*A(1,3)/tt(1)^2;
-(A(1,2) + 2*A(1,3))/tt(1) + (A(2,2) - 2*A(2,3))/tt(2);
-2*A(2,3)/tt(2)^2 ];
x = inv(B)*b;
% Coeficientes 4 y 5 de cada segmento.
A(1,4) = x(1);
A(1,5) = x(2);
A(2,4) = x(3);
A(2,5) = x(4);
end;
% Para cuando el motor no se mueve.
else
caso = 2;
tt = [0 0 0];
A = zeros(2,5);
end;
return
⇒ El lector debe notar la redefinición del segundo elemento del vector TT que
define los intervalos de tiempo de aceleración, velocidad máxima y frenado en el caso 1,
ajustando la aproximación que se había realizado con la variable TTOT.
La función PLANIFICADOR hace uso de las funciones definidas anteriormente,
y permite obtener los polinomios )(),(),( tqtqtq iii
. Debe observarse que en el interior
de esta función se encuentran los parámetros de los actuadores del robot. Se han
introducido valores estándar para articulaciones robotizadas como son velocidades
máximas de π/3 radianes/seg. (1.0472 rad/seg.) y tiempos de aceleración y frenado de
0.1 seg.](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-105-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 5 .- Pág. 14
% PLANIFICADOR Planificador de trayectorias con interpolador 4-3-4.
%
% [T,POS_PLAN, VEL_PLAN, ACE_PLAN]=PLANIFICADOR(Q1,Q2) calcula las
matrices
% de posición, velocidad y aceleración de los puntos nudo que representan
% la planficiación de trayectorias entre los punto Q1 y Q2 cumpliendo con
% las restricciones de trayectoria suave y prestaciones de los actuadores.
% Utiliza los polinomios 4-3-4 en los tres segmentos de trayectoria.
%
% Ver también CALCULOCOEF, SINCRONIZADOR, EVALPOS, EVALVEL, EVALACEL.
function [t, pos_plan, vel_plan, ace_plan] = planificador(q1,q2)
%**********************parámetros de los accionamientos**************
%---------------------------------------------------------------------
% Especificaciones de los tiempos de arranque y frenado de cada motor.
%---------------------------------------------------------------------
tmotor = 0.1*ones(6,2);
%---------------------------------------------------------------------
%Velocidades Maxima de cada motor.
%---------------------------------------------------------------------
velmax = [1.0472;1.0472;1.0472;1.0472;1.0472;1.0472];
%**********************planificador coordinado***********************
%---------------------------------------------------------------------
% Inicialización de los vectores posicion - Velocidad - aceleracion.
%---------------------------------------------------------------------
q = zeros(6,1);
q0 = [q1 q q];
qf = [q2 q q];
%---------------------------------------------------------------------
% Sincronización de los motores para que realizen un movimiento
coordinado
%---------------------------------------------------------------------
[velo2,tmaximo]=sincronizador(q0,qf,velmax);
%---------------------------------------------------------------------
%Inicialización de la escala de tiempo y las matrices.
%---------------------------------------------------------------------
t = 0:0.01:(tmaximo+0.15);
% +0.15 se suma con el fin de aumentar el intervalo de tiempo y
muestrear
% todo el intervalo de frenado de la articulación, asumiendo las
% aproximaciones realizadas en la función SINCRONIZADOR.
ini=zeros(length(t),1);
pos_plan(:,1)=ini;
vel_plan(:,1)=ini;
ace_plan(:,1)=ini;
%---------------------------------------------------------------------](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-106-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 5 .- Pág. 15
% Cálculo de los coeficientes de los polinomios y evaluación de los
% polinomios de interpolación.
%---------------------------------------------------------------------
for i = 1:6
[caso,A,tt] = calculocoef(i,velo2,q0,qf,tmotor);
posi=evalpos(t,tt,caso,A);
pos_plan(:,i)=posi';
ve=evalvel(t,tt,caso,A);
vel_plan(:,i)=ve';
ace=evalacel(t,tt,caso,A);
ace_plan(:,i)=ace';
end;
return
Finalmente se han desarrollado unas funciones que evalúan los polinomios en
los puntos estudiados de acuerdo a los coeficientes calculados, permitiendo la
representación gráfica de los resultados. Estas funciones son EVALPOS, EVALVEL y
EVALACEL. Se muestra a continuación la función EVALPOS que evalúa la posición
de la articulación. Las otras funciones las proporcionará el profesor en durante la sesión
de prácticas.
% EVALPOS Funcion que evalua el polinomio de la funcion de posición de
% acuerdo al caso y al tiempo.
% POS=EVALPOS(T,TT,CASO,A) evalúa el polinomio de aceleración.
% A matriz 5x3 que contiene los coeficientes de los polinomios
interpolados.
% T vector tiempo normalizado.
% TT segmentos de tiempo de aceleración, velocidad máxima y deceleración.
% caso=1: Cada motor logra alcanzar su velocidad maxima.
% caso=2: No hay tiempo de alcanzar la velocidad maxima de cada motor.
%
% Ver también PLANIFICADOR, CALCULOCOEF, SINCRONIZADOR, EVALVEL, EVALACEL.
function pos = evalpos(t,tt,caso,A)
for i = 1:length(t)
if caso == 1
if (t(i) <= 0)
p = A(1,1);
elseif (t(i)>0)&(t(i)<=tt(1))
ti = t(i)/tt(1);
p = A(1,1)+ A(1,2)*ti+ A(1,3)*ti^2+A(1,4)*ti^3+A(1,5)*ti^4;
elseif (t(i)>tt(1))&(t(i)<=tt(2)+tt(1))
ti = (t(i)-tt(1))/tt(2);
p = A(2,1)+A(2,2)*ti;
elseif (t(i)>tt(2)+tt(1))&(t(i)<=tt(3)+tt(2)+tt(1))
ti = (t(i)-tt(2)-tt(1))/tt(3);
p = A(3,1)+A(3,2)*(ti-1)+A(3,3)*(ti-1).^2+A(3,4)*(ti-
1).^3+A(3,5)*(ti-1).^4;
elseif (t(i)>tt(3)+tt(2)+tt(1))
p = A(3,1);
end;
elseif caso==2
if (t(i) <= 0)
p = A(1,1);](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-107-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 5 .- Pág. 16
elseif (t(i)>0)&(t(i)<=tt(1))
ti = t(i)/tt(1);
p = A(1,1)+ A(1,2)*ti+ A(1,3)*ti^2+A(1,4)*ti^3+A(1,5)*ti^4;
elseif (t(i)>tt(1))&(t(i)<=tt(2)+tt(1))
ti = (t(i)-tt(1))/tt(2);
p = A(2,1)+A(2,2)*(ti-1)+A(2,3)*(ti-1).^2+A(2,4)*(ti-
1).^3+A(2,5)*(ti-1).^4;
elseif (t(i)>tt(2)+tt(1))
p = A(2,1);
end;
end;
pos(i)=p;
end;
return
Para comprobar el funcionamiento del código desarrollado se sugiere al lector ejecute
varias veces el fichero ejemplo.m que se encuentra en el directorio /Capítulo5 en el que
se generan dos vectores aleatorios que definen dos posiciones de un robot de 6 grados
de libertad, se calculan las trayectorias articulares haciendo uso de las funciones
estudiadas y se grafican los polinomios )(),(),( tqtqtq iii
. Debe notarse que para cada
ejecución, y dependiendo del máximo recorrido que deba efectuar la articulación más
desfavorable en este sentido, el tiempo que tardará en alcanzar la posición final es
diferente.
Ejemplo 5.1
Al ejecutar ejemplo.m se obtiene las gráficas de la posición, velocidad y
aceleración de las seis articulaciones de un robot de 6 gdl que evolucione entre dos
puntos aleatorios de su espacio de trabajo.
%----------------------------------------------------------
%----programa de prueba del software de planificación -----
%---- interpolación 4-3-4 -----
%----------------------------------------------------------
clear
%---------------------------------------------------------------------
% q1 y q2 son las coordenadas articulares inicial y final
%---------------------------------------------------------------------
disp([' ']);
disp([' Vectores q1 y q2 de las coordenadas articulares ']);
disp([' inicial y final. ']);
q1 = rand(6,1)
q2 = rand(6,1)
%---------------------------------------------------------------------
% Llamada a la función PLANIFICADOR
%---------------------------------------------------------------------
[t,pos, vel, ace] = planificador(q1,q2);](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-108-320.jpg)

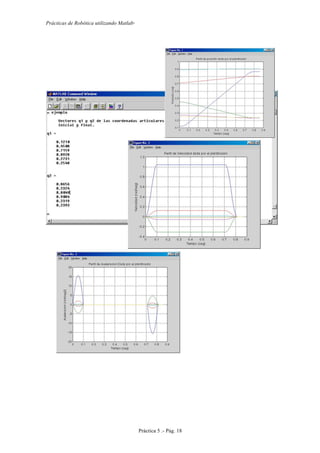
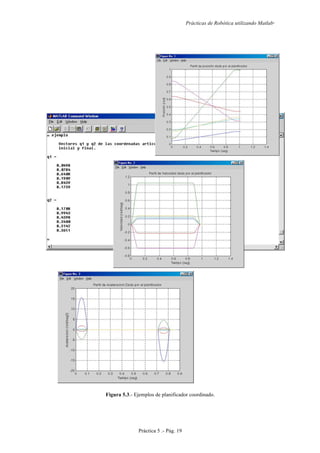
![Prácticas de Robótica utilizando Matlab®
Práctica 5 .- Pág. 20
⇒ Se recomienda al lector que realice varios ejemplos observando que la
velocidad máxima siempre es la nominal de la articulación que mayores solicitudes
temporales tiene. Es igualmente recomendable que el estudiante introduzca vectores q1
y q2 definidos por él, que definan posiciones fácilmente identificables y que observe las
gráficas que resultan. Por ejemplo puede hacerse partir todas las articulaciones de su
posición cero (q1=[0 0 0 0 0 0 ]T
) y observar lo que sucede con cada articulación.
5.5.-PRACTICA. Animación de la trayectoria.
En este apartado se ilustra la herramienta teórica que se ha estudiado con los
ejemplos de los robots de 4 y 6 gdl que sirven de apoyo a lo largo del libro.
Ejemplo 5.2
En este ejemplo se implementa en MatLab
un planificador de trayectorias
coordinado. Se utiliza el robot rotacional de 6 gdl de la figura 5.4
Basándose en el esquema general presentado en el apartado 5.2, el primer paso
es estudiar las necesidades de movimiento, especificar un punto inicial (posición y
orientación) y un punto final (posición y orientación) y obtener las coordenadas
articulares correspondientes a estos puntos nudo. Para ello se utilizan las funciones
desarrolladas en la práctica 2 DENAVIT y INVERSEKINEMATIC6.
Hay que recordar en este punto lo estudiado
en la práctica 2 sobre la posible existencia de
múltiples soluciones en la cinemática inversa
debido a las posibles configuraciones del codo y la
muñeca del manipulador.
Se parte de dos puntos del espacio de
trabajo del robot definidos por :
P1=(x1,y1,z1,α1,β1,γ1)
P2=(x2,y2,z2,α2,β2,γ2)
A partir de estos puntos se obtienen los vectores en
coordenadas articulares correspondientes a los
puntos inicial y final del camino que se quiere
recorrer.
s
a
n
Figura 5.4.- Robot
rotacional de 6 gdl](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-112-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 5 .- Pág. 21
El siguiente ejemplo muestra como se ha utilizado la función
INVERSEKINEMATIC6 para obtener los vectores q1 y q2 a partir de unas matrices
homogéneas T1 y T2 que definen en coordenadas cartesianas la posición y orientación
de dos puntos en el espacio de trabajo del robot.
A partir de los vectores q1 y q2 se realiza un ejecuta el planificador que me
proporciona los polinomios )(),(),( tqtqtq iii
con las trayectorias articulares.
» T1=[0 1 0 -0.3;1 0 0 -0.2;0 0 1 0.6; 0 0 0 1]
T1 =
0 1.0000 0 -0.3000
1.0000 0 0 -0.2000
0 0 1.0000 0.6000
0 0 0 1.0000
» T2=[0 0 1 -0.3;0 1 0 0.4;1 0 0 0.5; 0 0 0 1]
T2 =
0 0 1.0000 -0.3000
0 1.0000 0 0.4000
1.0000 0 0 0.5000
0 0 0 1.0000
» q1=inversekinematic6(T1,-1,1)
q1 =
-2.5536
0.7137
-0.6729
0.0000
-0.0408
-0.9828
» q2=inversekinematic6(T2,-1,1)
q2 =
2.3306
0.6579
-0.2558
-2.2892
1.8437
-0.2990
»
» [t,pos, vel, ace] = planificador(q1,q2);
»](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-113-320.jpg)
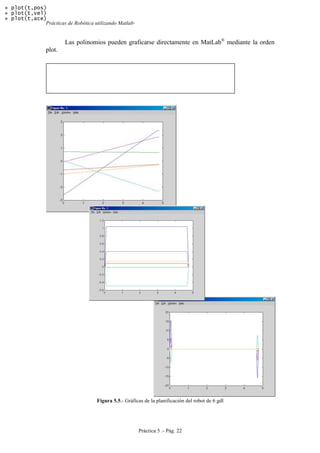





![Prácticas de Robótica utilizando Matlab®
Práctica 6 .- Pág. 5
Motor 1
Para realizar el sintonizado del motor 1 se ha desarrollado en Simulink
el modelo que
se encuentra en el fichero sintonizar1d4.mdl. Este fichero contiene el esquema de
control en bucle cerrado de la primera articulación que permite ajustar su regulador PID
para que la respuesta satisfaga las especificaciones. Si se ejecuta desde el entorno de
Matlab “sintonizar1d4” aparecerá en pantalla la aplicación para el sintonizado de la
primera articulación, que se muestra en la figura 6.2.
Figura 6.2. Herramienta desarrollada en Simulink
para realizar el sintonizado de la primera articulación.
Para obtener la aceleración de cada articulación se ha desarrollado en Matlab
la función
dindir4gdl.m; que calcula la aceleración de cada articulación cuando el robot transporta
una determinada carga en función de la posición y velocidad actual de la articulación y
de su fuerza/par de entrada. Esta función hace uso de la función walkerorin4.m,
explicada en la práctica 3. El código fuente de dindir4gdl.m se muestra a continuación:
% DINDIR4GDL Dinámica directa de un robot de 4GDL.
% QPP = DINDIR4GDL(ENTRADA) calcula el vector 4x1 de aceleración de
% cada articulación utilizando el tercer método de Walker y Orin.
% ENTRADA(1:4) representa el par de entrada a cada articulación.
% ENTRADA(5:8) es la posición de cada articulación. ENTRADA(9:12)
% es la velocidad de cada articulación.
%
% Ver también WALKERORIN4.
function qpp = dindir4gdl(entrada)
tau = entrada(1:4); % Par de entrada a cada articulación
q = entrada(5:8); % Posición de cada articulación
qp = entrada(9:12); % Velocidad de cada articulación
% Parámetros de la carga
masaext = 10;
inerciaext = [0.0167 0 0;0 0.0167 0;0 0 0.0167];
% Se convierten los pares de la articulación 2 y 3 en fuerzas.
n = 0.85; % Eficiencia husillo
p = 0.025; % Paso del husillo (mm)
tau(2:3) = 2*pi*tau(2:3)/p;
% Se calcula la aceleración utilizando el método de Walker y Orin.
qpp = walkerorin4(q,qp,tau,masaext,inerciaext);](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-120-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 6 .- Pág. 6
En la función dindir4gdl.m el par proporcionado por los motores 2 y 3 se convierte a
fuerza, ya que las articulaciones 2 y 3 son prismáticas, utilizando la siguiente ecuación:
p
nτπ2
F =
donde τ es el par (Nm), p es el paso del husillo (m) y n es la eficiencia del husillo.
Las entradas al esquema de control son:
- El escalón de posición que se aplica a la primera articulación. El escalón es de 0.08
rad y, puesto que para esta articulación es independiente que sea positivo o negativo,
se ha considerado positivo. El valor de la posición de esta primera articulación en la
peor configuración del robot es 0 rad, por lo tanto el escalón será de 0 rad a 0.08 rad.
- Los pares del resto de motores. Puesto que los actuadores de las articulaciones que
no están siendo sintonizadas son apagadas, los pares del resto de motores son nulos.
- La posición del resto de articulaciones en su peor configuración.
- La velocidad de las restantes articulaciones. La velocidad de las restantes
articulaciones siempre será cero, puesto que sus actuadores están apagados.
El bloque PID representa a un regulador convencional PID con la siguiente función de
transferencia:
Ds
s
I
PsGPID ++=)(
Asignando los valores adecuados a P, I y D se conseguirá que la respuesta del sistema
sea la deseada.
En el bloque correspondiente al motor de la articulación 1 se deben colocar los datos de
los parámetros del motor que se seleccionó en la practica 4 para esa articulación. Estos
datos se muestran en la tabla 6.2.
Articulación Nombre Motor R(Ω) L(mH) KT (Nm/A) KV (V/rad/s) Imáx (A)
1 DA23GBB 0.8 0.93 0.058 0.058 18.5
Tabla 6.2. Valores de los parámetros del motor utilizado para la primera articulación.
Los bloques Ordena Pares, Ordena Posiciones y Ordena Velocidades, simplemente
indican el orden del vector de pares, posiciones y velocidades del robot. En este caso los
vectores poseen el orden adecuado, ya que se está sintonizando la primera articulación,
de manera que el orden que indicaremos en los tres selectores será [1 2 3 4]. Sin
embargo, veremos que esto no es así para el sintonizado del resto de articulaciones.](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-121-320.jpg)


![Prácticas de Robótica utilizando Matlab®
Práctica 6 .- Pág. 9
En los bloques Ordena Pares, Ordena Posiciones y Ordena Velocidades se indica el
orden del vector de pares, posiciones y velocidades del robot. El orden que indicaremos
en los tres selectores será [2 1 3 4].
Puesto que se está ajustando la segunda articulación, a continuación del bloque Robot 4
GDL, se indicará en el selector que se elige la aceleración de la segunda articulación. En
el bloque Integrador Aceleración especificamos que la condición inicial es cero, ya que
la velocidad inicial de esta articulación es de 0 m/s. En el bloque Integrador Velocidad
se indica que la condición inicial es 1, puesto que la posición inicial de la articulación es
1 m.
Un posible regulador que proporciona que la respuesta de la segunda articulación se
ajuste a las especificaciones establecidas es el siguiente:
ssPIDG 6300)( +=
Si se realiza la simulación del modelo se obtiene la gráfica que muestra como varía la
posición de la articulación 2 ante el escalón introducido. Como se puede apreciar en la
gráfica, al igual que en el caso anterior, con el regulador escogido se satisfacen los
requerimientos impuestos. Ver figura 6.5.
Figura 6.5. Posición de la articulación 2 ante entrada en escalón.
Motor 3
Para realizar el sintonizado del motor 3 se utiliza el modelo implementado en Simulink
que se encuentra en el fichero sintonizar3d4.mdl. Este modelo contiene el esquema de
control en bucle cerrado de la tercera articulación que permite ajustar su regulador PID
para que la respuesta satisfaga las especificaciones.
Las entradas al esquema de control son:
- El escalón de posición que se aplica a la tercera articulación. Este escalón es de 100
mm. El valor de la posición de esta articulación en la peor configuración del robot es](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-124-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 6 .- Pág. 10
1.2 m. Al igual que en el caso anterior, el mayor requerimiento de par se produce
cuando el escalón es positivo. Sin embargo como la articulación posee su extensión
máxima, el escalón no es realizable físicamente, por lo que se introducirá un escalón
negativo. Por lo tanto el escalón será de 1.2 m a 1.1 m.
- Los pares del resto de motores. Al igual que en los casos anteriores, los pares del
resto de motores son nulos.
- La posición del resto de articulaciones en su peor configuración.
- La velocidad de las restantes articulaciones. Como en los casos anteriores, la
velocidad de las restantes articulaciones es cero.
En el bloque correspondiente al motor de la articulación 3 se deben colocar los datos de
los parámetros del motor que se seleccionó en la práctica 4 para esa articulación.
Articulación Nombre Motor R(Ω) L(mH) KT (Nm/A) KV (V/rad/s) Imáx (A)
3 DA23GBB 0.8 0.93 0.058 0.058 18.5
En los bloques Ordena Pares, Ordena Posiciones y Ordena Velocidades se indica el
orden del vector de pares, posiciones y velocidades del robot. El orden que indicaremos
en los tres selectores será [2 3 1 4].
Puesto que se está ajustando la tercera articulación, a continuación del bloque Robot 4
GDL, se indicará en el selector que se elige la aceleración de la tercera articulación. En
el bloque Integrador Aceleración especificamos que la condición inicial es cero, ya que
la velocidad inicial de esta articulación es de 0 m/s. En el bloque Integrador Velocidad
se indica que la condición inicial es 1.2, puesto que la posición inicial de la articulación
es 1.2 m.
Un posible regulador que proporciona que la respuesta de la segunda articulación se
ajuste a las especificaciones establecidas es el siguiente:
ssPIDG 7.5200)( +=
Si se realiza la simulación del modelo se obtiene la gráfica que muestra como varía la
posición de la articulación 3 ante el escalón introducido. Como se puede apreciar en la
gráfica, al igual que en el caso anterior, con el regulador escogido se satisfacen los
requerimientos impuestos. Ver figura 6.6.](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-125-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 6 .- Pág. 11
Figura 6.6. Posición de la articulación 3 ante entrada en escalón.
Motor 4
Para realizar el sintonizado del motor 4 se utiliza el modelo que se encuentra en el
fichero sintonizar4d4.mdl. Este modelo contiene el esquema de control en bucle cerrado
de la cuarta articulación que permite ajustar su regulador PID para que la respuesta
cumpla las especificaciones.
Las entradas al esquema de control son:
- El escalón de posición que se aplica a la cuarta articulación. El valor de la posición
de esta articulación en la peor configuración del robot es 0 rad. Para esta
articulación es independiente que el escalón sea positivo o negativo.
Consideraremos que el escalón es de 0 rad a 0.08 rad.
- Los pares del resto de motores. Al igual que en los casos anteriores, los pares del
resto de motores son nulos.
- La posición del resto de articulaciones en su peor configuración.
- La velocidad de las restantes articulaciones. Como en los casos anteriores, la
velocidad de las restantes articulaciones es cero.
En el bloque correspondiente al motor de la articulación 4 se deben colocar los datos de
los parámetros del motor que se seleccionó en la práctica 4 para esa articulación.
Articulación Nombre Motor R(Ω) L(mH) KT (Nm/A) KV (V/rad/s) Imáx (A)
4 DB17CDB 6.9 1.28 0.035 0.035 3.6
En los bloques Ordena Pares, Ordena Posiciones y Ordena Velocidades se indica el
orden del vector de pares, posiciones y velocidades del robot. El orden que indicaremos
en los tres selectores será [2 3 4 1].
Puesto que se está ajustando la cuarta articulación, a continuación del bloque Robot 4
GDL, se indicará en el selector que se elige la aceleración de la cuarta articulación. En
el bloque Integrador Aceleración especificamos que la condición inicial es cero, ya que
la velocidad inicial de esta articulación es de 0 rad/s. En el bloque Integrador Velocidad](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-126-320.jpg)

![Prácticas de Robótica utilizando Matlab®
Práctica 6 .- Pág. 13
simulación se ha desarrollado en Simulink el modelo que se encuentra en el fichero
simulador4.mdl. Ver figura 6.8.
Velocidades
Posiciones
SIM ULACIÌ N DE LA TRAY ECTORIA EN LÈNEA RECTA DEL ROBOT DE 4GDL
m at_q
T o Workspace
Sum 4
Sum 3
Sum 2
Sum 1
Saturation 4
Saturation 3
Saturation 2
Saturation 1
M AT LAB
Function
Robot 4GDL
[0 -0.6 0.5]
Posición Inicial
[0 -1 1.2]
Posición Final
Planificación
Planificación de
trayectorias
M ux
Pares
PID
PID 4
PID
PID 3
PID
PID 2
PID
PID 1
M ux
M ux
Volt
Vel
Par
M otor 4
Volt
Vel
Par
M otor 3
Volt
Vel
Par
M otor 2
Volt
Vel
Par
M otor 1
1/s
Integrator1
1/s
Integrator
Graficas
Dem ux
Dem ux
Dem ux
Dem ux1
M AT LAB
Function
Cinem ática
Inversa
25
Am plificador 4
25
Am plificador 3
25
Am plificador 2
25
Am plificador 1
Figura 6.8. Simulador del robot de 4 GDL.
Como puede apreciarse en la figura 6.8, para realizar la simulación se utiliza un
esquema de control desacoplado, de forma que cada articulación posee un regulador
PID. Los valores de los motores del robot que se utilizan para realizar la simulación son
aquellos que se emplearon en el proceso de sintonizado mostrado en el ejemplo 6.5.
Estos valores se recogen en la tabla 6.4. Así mismo los valores de los reguladores PID
son los que se obtuvieron en el ejemplo 6.1, que se muestran en la tabla 6.5.
Articulación Nombre Motor R(Ω) L(mH) KT (Nm/A) KV (V/rad/s) Imáx (A)
1 DA23JBB 0.39 0.65 0.054 0.054 25.3
2 DA34HBB 1.6 1.56 0.176 0.176 23.7
3 DA23GBB 0.8 0.93 0.058 0.058 18.5
4 DB17CDB 6.9 1.28 0.035 0.035 3.6
Tabla 6.4. Motores utilizados en el simulador del robot de 4 GDL.
Articulación P I D
1 90 0 1.6
2 300 0 6
3 200 0 5.7
4 100 0 0
Tabla 6.5. Valores de los reguladores del robot de 4 GDL.
El bloque Robot 4 GDL representa la dinámica directa del robot de 4 GDL. Como se
mostró en el ejemplo 6.3, para realizar la dinámica directa se ha desarrollado en Matlab
la función dindir4gdl.m. Esta función calcula la aceleración de cada articulación
cuando el robot transporta una determinada carga en función de la posición y velocidad
actual de la articulación y de su fuerza/par de entrada.](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-128-320.jpg)

![Prácticas de Robótica utilizando Matlab®
Práctica 6 .- Pág. 15
Esta función proporciona las coordenadas articulares del robot del instante actual de
simulación a partir del instante de tiempo y de la posición inicial y final expresadas en
coordenadas cartesianas. La función realiza una planificación de trayectorias en línea
recta entre la posición inicial y la final. Para ello divide la trayectoria en un número de
segmentos que viene impuesto por los parámetros con los que se desea simular en
Simulink:
nintegraciódeintervalo
simulacióndetiempo
segmentosnº =
En función del instante de simulación calcula qué posición cartesiana debe tener el
extremo del robot y, realizando la cinemática inversa del robot mediante la función
cininv4gdl.m, calcula las variables articulares del robot. El código fuente de la función
cininv4gdl.m es el siguiente:
% CININV4GDL Cinemática inversa de un robot de 4GDL.
% Q = CININV4GDL(ENTRADA) devuelve el vector 4x1 de coordenadas
% articulares que contiene la solución cinemática inversa.
% ENTRADA es un vector 3x1 que representa la posición expresada
% en coordenadas cartesianas.
%
% Ver también INVERSEKINEMATIC4.
function q = cininv4gdl(entrada)
% Posición cartesiana
p = entrada;
% Orientación deseada en el extremo del robot
n = [1 0 0]';
s = [0 0 -1]';
a = [0 1 0]';
% Matriz con la orientación y posición deseadas en el extremo del robot
T = [n s a entrada];
% Se calculan las coordenadas articulares
q = inversekinematic4(T);
La función cininv4gdl.m utiliza la función inversekinematic4.m obtenida en la práctica 2
para realizar la cinemática inversa del robot de 4 GDL. Como se puede apreciar en el
código fuente presentado, se especifica la orientación deseada en el extremo del robot.
Por lo tanto la orientación del extremo del robot permanecerá fija durante toda la
planificación. Para que un robot pueda posicionarse en cualquier punto con cualquier
orientación necesita un mínimo de 6 GDL. Este robot es de 4 GDL, por lo que existen
trayectorias que no pueden realizarse si la orientación del extremo es fija. Para realizar
cualquier trayectoria correctamente sería necesario modificar en cada momento la
orientación del extremo. Es decir, habría que realizar una planificación de la posición
del extremo, así como de su orientación. Sin embargo, como la única finalidad en este
apartado es simular el comportamiento del robot de 4 GDL, la orientación del extremo
permanecerá fija, de forma que se realizarán trayectorias en las que el extremo no
cambie su orientación.](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-130-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 6 .- Pág. 16
El bloque Cinemática Inversa calcula la cinemática inversa de la posición cartesiana
inicial de la trayectoria mediante la función cininv4gdl.m. Este cálculo es necesario, ya
que el integrador del modelo que obtiene las posiciones articulares del robot a partir de
las velocidades, necesita como condición inicial las variables articulares
correspondientes a la posición cartesiana inicial del extremo del robot.
Con la finalidad de poder efectuar una animación de la trayectoria del extremo del robot
desde Matlab se guarda la posición de cada articulación en la matriz mat_q. Esta matriz
posee una fila por cada instante de simulación y una columna por cada variable
articular.
Para realizar la simulación de la trayectoria en primer lugar es necesario configurar los
parámetros de la simulación. Los valores seleccionados de los parámetros son los que se
muestran en la figura 6.10. Es muy importante destacar que el tipo de paso seleccionado
del Solver debe ser fijo y además el valor del paso debe coincidir con el intervalo de
integración especificado en la función planifica4.m. Así mismo, el tiempo de
simulación deber ser idéntico al considerado en dicha función.
Figura 6.10. Parámetros para realizar la simulación del robot de 4 GDL.
Una vez que se han establecido los parámetros de simulación de Simulink
, ya puede
realizarse la simulación del modelo. Una vez finalizada la simulación, podremos, desde
el entorno de Matlab
, realizar una animación para comprobar visualmente que el robot
realiza la trayectoria deseada. Para efectuar la animación se utilizará la función
desarrollada en Matlab
animacion4.m. El código de esta función se muestra a
continuación:
% ANIMACION4 Animación de la trayectoria de un robot de 4 GDL
% ANIMACION(MAT_Q) realiza la animación de la trayectoria, expresada
% en la matriz MAT_Q, de un brazo robot de 4 GDL. MAT_Q contiene 4 filas
% y una columna para cada disposición del robot.
%
% Ver también DRAWROBOT3D4.
function animacion4(mat_q)
% Parámetros Denavit-Hartenberg del robot. Los parámetros correspondientes
% a variables articulares aparecen con valor 0
teta = [0 0 0 0 ];](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-131-320.jpg)
![Prácticas de Robótica utilizando Matlab®
Práctica 6 .- Pág. 17
d = [0.4 0 0 0.2];
a = [0 -0.1 0 0 ];
alfa = [0 -pi/2 0 0 ];
% Vector de posicion (x, y, z) del sistema de coordenadas de referencia
x0 = 0; y0 = 0; z0 = 0;
% Se dibuja el sistema de coordenadas de referencia. Se asigna el modo XOR
para borrar
% sólo el robot dibujado anteriormente. Se utiliza un grosor de línea de 2
unidades
p = plot3(x0,y0,z0,'EraseMode','xor','LineWidth',2);
% Se asigna una rejilla a los ejes
grid;
% Se establecen los límites de los ejes
axis([-1.5 1.5 -1.5 1.5 0 1.5]);
% Mantiene el gráfico actual
hold on;
% Número de columnas de la matriz
n = size(mat_q,2);
% Se dibuja la disposición del robot correspondiente a cada columna
for i=1:n
% Variables articulares del brazo robot
q1 = mat_q(1,i);
q2 = mat_q(2,i);
q3 = mat_q(3,i);
q4 = mat_q(4,i);
% Matrices de transformación homogénea entre sistemas de coordenadas
consecutivos
A01 = denavit(q1, d(1), a(1), alfa(1));
A12 = denavit(teta(2), q2, a(2), alfa(2));
A23 = denavit(teta(3), q3, a(3), alfa(3));
A34 = denavit(q4, d(4), a(4), alfa(4));
% Matrices de transformación del primer sistema al correspondiente
A02 = A01 * A12;
A03 = A02 * A23;
A04 = A03 * A34;
% Vector de posicion (x, y, z) de cada sistema de coordenadas
x1 = A01(1,4); y1 = A01(2,4); z1 = A01(3,4);
xi = x1; yi = y1; zi = z1 + q2;
x2 = A02(1,4); y2 = A02(2,4); z2 = A02(3,4);
x3 = A03(1,4); y3 = A03(2,4); z3 = A03(3,4);
x4 = A04(1,4); y4 = A04(2,4); z4 = A04(3,4);
% Se dibuja el robot
x = [x0 x1 xi x2 x3 x4];
y = [y0 y1 yi y2 y3 y4];
z = [z0 z1 zi z2 z3 z4];
set(p,'XData',x,'YData',y,'ZData',z);
% Se fuerza a MATLAB a actualizar la pantalla
drawnow;
end
Para realizar la animación simplemente se ejecutará desde Matlab:
» animacion4(mat_q')](https://image.slidesharecdn.com/practicasderoboticautilizandomatlab-roque-151015202716-lva1-app6891/85/Practicas-de-robotica-utilizando-matlab-Roque-132-320.jpg)
