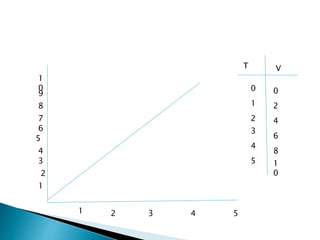
El documento trata sobre el tema de la cinemática. Explica conceptos como movimiento rectilíneo uniforme, movimiento uniformemente acelerado, caída libre, movimiento parabólico y movimiento circular uniforme. Incluye fórmulas clave para calcular distancias, velocidades, tiempos y otras variables en diferentes tipos de movimiento.

1. Instituto Técnico Industrial
Multipropósito
Laura Rojas
11-1

2.  (Del griego Kivew, Kineo, Movimiento) es la
rama de la física que estudia las leyes del
movimiento de los cuerpos sin considerar las
causas que la originan (las fuerzas) y se
limita, esencialmente, al estudio de la
trayectoria en función del tiempo.

3. 1. Velocidad constante
2. No hay Aceleración
3. Se recorren espacios iguales en tiempos
iguales
4. X:V°t+X°
5. Si no se expresa X°:0

4.  Un auto se mueve a velocidad de 12m/s
constante durante 5 seg. Que distancia
recorre ¿Cuánto se desplaza si es en línea
recta?
 X:V°t+X° X:(12m/seg)(5seg)+(0m)
 X°:0 X: 60m+0m:60m
 V:12m/s R/ recorre 60m
 T:5seg

5.  60km/h :V T: 10 min
 Hora: 60 min
 X:(60km/60min).(10min)
 1km.10: 10km

6.  Un joven que vive a 2,5km del colegio sale a
las 6:10Am y debe llegar a las 6:30Am, de lo
contrario no puede ingresar a la clase de
física
Si en joven sabe que debe asistir a que
velocidad mínimo (constante) debe caminar
para llegar justo a tiempo.

7. 2,5km
6:10Am
6:30Am
2,5km/20min.(1min/60seg):2,5Km/1200s.(100
0,/1km):2500m/1200seg.
Tiempo a recorres en 20min es 2,500m en
1,200seg
20 Min.

8.  Aceleración Constante
 La velocidad cambia de manera uniforme

9.  Un movimiento que parte del resposo
acelerado a razón de 2m/s2 cuál, es su
velocidad a los 0,1,2,3,4,5 seg.
A:2m/s2 V:(M/S)
V: at+V°
V: (2m/s2)t+0
V:(2m/s)t V:26m/s

10. 1 2 3 4 5
1
2
3
4
5
6
7
8
9
1
0
T V
0
1
2
3
4
5
0
2
4
6
8
1
0

11.  Un móvil con velocidad inicial 3m/s acelera a
razón de 2m/s2 determine su velocidad a los
0,1,2,3,4,5 seg.
 V:at+v°
 V:(2m/s2).Tr3m/s
 V:2.t+3

12. 1 2 3 4 5
1
2
3
4
5
6
7
8
9
10
11
12
1
3
T V
0
1
2
3
4
5
3
5
7
9
11
1
3

13.  Un fenómeno producido para la tracción
gravitacional de la tierra sobre los cuerpos
La caída libre es un caso especial del
movimiento Uniforme mente acelerado
FORMULAS:
V:V°+at V:V°+gt
X:1/2at2+v°t+X°
Y2:1/2gt2+V°t+y°
V2: V°2+2ax V2:V°2+2gy

14.  Para un cuerpo en la caída libre la v°:0
V°: Velocidad Inicial
1.Ejemplo
Desde una altura de 30mts se deja caer un
cuerpo cuanto tiempo tarda en llegar al piso.
Con que velocidad golpea el piso

15. 1.Datos Preg.
Y: 30m T:?
V°: 0 V:?
G: 9,8m/s2
Y:1/2gt2+v°t+Y°
30m:1/2(98m/s2).t+o.t
30m:1/2(9,8m/s2)t2

16. (30m).2/(9,8m/s2):T
60m/9,8m/s2:T
6,1seg2: T2
Raíz 6,1s2: T
2,46 segundos: T
V:V°+gt V:V°+gt
V:0+(9,8m/s2) 2,46seg
V:(9,8m/s2)/2,46seg : 3,9m
Raíz 3,9: 19vf

17.  Desde una altura de 50mts se deja caer un
cuerpo cuanto tiempo tarda en llegar al
piso?¿con que velocidad golpea el piso?
Datos Preg
Y: 50m T:?
G:9,8m/s2 V:?
V:0

18.  Y:1/2gt2+V°t+y°
50m:1/2(9,8m/s2).t+o.t
50m:1/2(9,8m/s2)t2
(50m).2/(9,8m/s2): t2
100m/9,8m/s2:t
10,2s2:t
Raíz 10,1s2:t
3,19 seg.:t

19.  V:V°+gt
 V:0+(9,8m/s2) 3,19seg
 V:(9,8m/s2)/3,19seg: 3,07m
 Raíz 3,07m: 1,75m
V:V°+gt
V:0+(9,8m/s2).3,19s
V:31,26m/s

20.  El movimiento de una parabola o
semiparabolico (lanzamiento Horizontal) se
puede considerar como la posición de un
avance horizontal rectilíneo uniforme y la
caída libre de un cuerpo en reposo.
El movimiento semiparabolico es el
movimiento horizontal que se realiza en
diferentes objetos

22.  EJEMPLO 1: Una esfera es lanzada
horizontalmente desde una altura de 30m
con una velocidad inicial de 80m/s. calcular:

 El tiempo que dura la esfera en el aire.
 El alcance horizontal de la esfera.
 La velocidad con que la esfera llega al suelo.


23.  EJEMPLO 2: Desde un avión de guerra que
viaja con una velocidad horizontal de
420km/h, a una altura de 3500m, se suelta
una bomba con el fin de explotar
un campamento militar que está situado en la
superficie de la tierra. ¿Cuántos metros antes
de llegar al punto exacto del campamento,
debe ser soltada la bomba para dar con el
blanco?

25.  Se denomina movimiento parabólico al
realizado por un objeto cuya trayectoria
describe una parábola . Se corresponde con la
trayectoria ideal de un proyectil que se mueve
en un medio que no ofrece resistencia al
avance y que está sujeto a un campo
gravitorio uniforme.

26.  Rmax:(v°2.sen(2.@))/g
 Rmax: Alcance máximo del proyectil en el eje
x
V°: Velocidad inicial del proyectil
Sen: Entidad trigonométrica
@:Angulo de salida del proyectil
G: gravedad

27.  Se patea un balón de fútbol con un ángulo de
37° con una velocidad de 20 m/s. Calcule:

 a) La altura máxima.
 b) El tiempo que permanece en el aire.
 c) La distancia a la que llega al suelo.
 d) La velocidad en X y Y del proyectil después
de 1 seg de haber sido disparado


28.  Datos
 Ángulo = 37°
 a) Ymax = ?
 d) Vx =?
 Vo = 20m/s
 b) t total = ?
 Vy = ?
 g= -9.8 m/s^2
 c) X = ?

29. Vox = Vo Cos a = 20 m/s Cos 37° = 15.97
m/s
Voy = Vo Se n a = 20 m/s Sen 37° = 12.03
m/sPaso 2
Calcular el tiempo de altura máxima ,
donde Voy = 0
Por lo tanto : t = (Vfy - Voy) / g = (0 -
12.03 m/s) / 9.8 = 1.22.seg.

30.  Paso 3
 Calcular a) la altura máxima:
 Ymax = Voy t + gt^2 / 2= 12.03 m/s ( 1.22s) +
(( -9.8m/s^2 )(1.22s)^2) / 2 = 7.38m

 Paso 4
 Calcular b) el tiempo total . En este caso solo se
multiplica el tiempo de altura máxima por 2,
porque sabemos que la trayectoria en este caso
es simétrica y tarda el doble de tiempo en caer el
proyectil de lo que tarda en alcanzar la altura
máxima.
 T total = tmax (2) = 1.22s (2) = 2.44 s.

31.  Paso 5
 Calcular el alcance máximo, para lo cual
usaremos esta formula:
 X = Vx t total = 15.97 m/s ( 2.44s) = 38.96
m.
 Paso 6
 Vfy = gt + Voy = (- 9.8) ( 1seg.) + 12.03 m/s
= 2.23 m/s
 Vfx = 15.97 m/s ,ya que esta es constante
durante todo el movimiento.

32.  Sea un proyetíl lanzado desde un cañón. Si
elegimos un sistema de referencia de modo
que la dirección Y sea vertical y positiva hacia
arriba, a y = - g y a x = 0. Además suponga
que el instante t = 0, el proyectil deja de
origen (X i = Y iVi. = 0) con una velocidad

35.  Vxi = Vi cos θ
 Vyi = Vi sen θi
 Como el movimiento de proyectiles es bi-
dimencional, donde ax = 0 y ay = -g, o sea con
aceleración constante, obtenemos las
componentes de la velocidad y las coordenadas
del proyectil en cualquier instante t, con ayuda
de las ecuaciones ya utilizadas para el M.R.U.A.
Expresando estas en función de las proyecciones
tenemos:
 X = Vxit = Vi cos θi t
 y = Vyi t + ½ at2
 Vyf = Vyi + at
 2ay = Vyf
2 - Vyi
2

36.  Altura Máxima que alcanza un proyectil.
 Tiempo de vuelo del proyectil:

37.  Alcance del proyectil :

38.  En cinematica, el movimiento
circular (también llamado movimiento
circunferencial) es el que se basa en un eje de
giro y radio constante, por lo cual
la trayectoria es una circunferencia. Si
además, la velocidad de giro es constante
(giro ondulatorio), se produce el movimiento
circular uniforme , que es un caso particular
de movimiento circular, con radio y centro
fijos y velocidad angular constante

39.  ejemplos de movimiento circular uniforme:
- un cuerpo celeste orbitando a otro en órbita
casi circular (ej: la tierra alrededor del sol).
- las hélices de un avión o helicóptero
- un auto haciendo una curva a velocidad
constante
- las ruedas de un vehículo (una bicicleta)
- una hormiga caminando por las paredes de una
botella.
- una nave espacial con gravedad artificial
basada en la rotación de la misma.
- un lavarropas

40.  ejemplos de movimiento uniformemente
acelerado:
- la frenada de un auto
- caída libre con resistencia del aire despreciable
- un ascensor
- un cohete con sus propulsores encendidos
- un cuerpo deslizándose por un plano inclinado
- un cuerpo de densidad constante, sumergido en
un medio de densidad constante (algo que se
hunde o flota), cayendo o acelerándose hacia
arriba de forma uniforme.

41.  Formulas…
 a = aceleración
v = velocidad
R = Radio de giro
T = Periodo (tiempo para dar una vuelta)
m = masa de cuerpo
Entonces:
a = (v^2 ) / R
v = 2 . Pi . R / T

42.  Otras formulas adicionales:
Sea:
Fc = Fuerza centrípeta
W = velocidad angular (radianes/seg)
Beta = Angulo recorrido desde el comienzo del giro
hasta el fin del giro.
S = longitud del arco de circunferencia recorrido
Entonces:
Fc = m . (v^2 ) / R
S = R . Beta
v = w. R