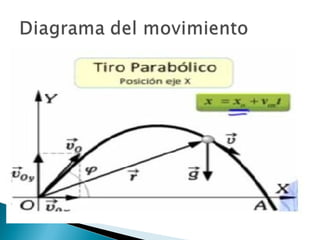
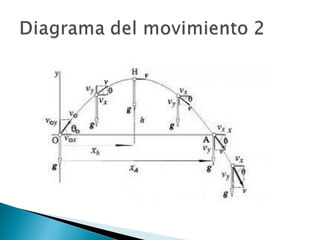
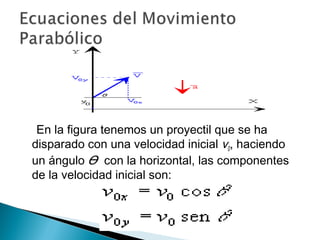
Este documento presenta las ecuaciones del movimiento parabólico, incluyendo la aceleración, velocidad y posición en función del tiempo, así como fórmulas para calcular la altura máxima y el alcance. Luego, propone 5 problemas de aplicación sobre lanzamientos de proyectiles en diferentes condiciones, requiriendo calcular variables como el tiempo de vuelo, desplazamiento horizontal, velocidad y altura máxima.

1. Docente: Dr. Máximo Valentín Montes

3. El tiro parabólico se puede estudiar
como la composición de dos
movimientos:
 Un movimiento rectilíneo uniforme
(M.R.U.) en la dirección del eje x.
 Un movimiento rectilíneo uniformemente
acelerado (M.R.U.A.) en la dirección del
eje y. ( a = g = 9.8 m/s

6. En la figura tenemos un proyectil que se ha
disparado con una velocidad inicial v0, haciendo
un ángulo ϴ con la horizontal, las componentes
de la velocidad inicial son:

7. ECUACIONES DEL MOVIMIETO
PARABOLICO
Magnitud Componente x Componente y
aceleración ax = 0 ay = -g
velocidad vx = v0x vy = v0y - gt
posición x = v0xt y = v0yt- (1/2)gt2

8. En el tiro parabólico son de interés la altura máxima y
el alcance (o desplazamiento horizontal) conseguido.
La altura máxima se alcanza cuando la componente
vertical vy de la velocidad se hace cero
. Como vy = v0y - gt, se alcanzará la altura máxima cuando
t = v0y/g.
Utilizando estos datos llegarás fácilmente a la conclusión de
que el valor de la altura máxima es:
ymax= v0y
2
/2g = (v0
2
/2g) sen2
α

9. El móvil estará avanzando horizontalmente a la
velocidad constante v0x durante el tiempo de
vuelo, que será 2t(siendo t el tiempo en
alcanzar la altura máxima) ya que el móvil tarda
lo mismo en subir que en bajar.
Por lo tanto el alcance es:
Xmax = v0x2t, es decir
alcance = Xmax = (v0
2
/g) sen 2α

12.  Problema 1
Un avión en vuelo horizontal a una
altura de 300 m y con una velocidad
de 60 m/s, deja caer una bomba.
Calcular el tiempo que tarda en llegar
al suelo, y el desplazamiento
horizontal de la bomba.

13. Problema 2
 Se lanza un cuerpo desde el origen con velocidad
horizontal de 40 m/s, y con una velocidad vertical
hacia arriba de 60 m/s. Calcular la máxima altura
y el alcance horizontal.

14. problema 3.
Resolver el ejercicio anterior, tomando como
lugar de lanzamiento la cima de una colina de 50
m de altura.

15. Problema 4.
Se lanza un proyectil desde una colina de 300 m
de altura, con una velocidad horizontal de 50 m/s,
y una velocidad vertical de -10 m/s (hacia abajo).
Calcular el alcance horizontal y la velocidad con
que llega al suelo.

16. Problema 5.
Un cañón dispara una bala desde lo alto de un
acantilado de 200 m de altura con una velocidad
de 46 m/s haciendo un ángulo de 30º por encima
de la horizontal. Calcular el alcance, el tiempo de
vuelo, y las componentes de la velocidad de la
bala al nivel del mar. Hallar también la altura
máxima. (Hallar primero, las componentes
horizontal y vertical de la velocidad inicial).