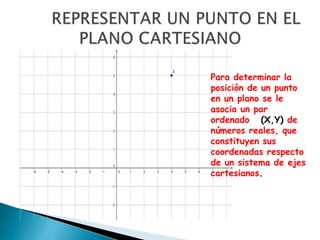
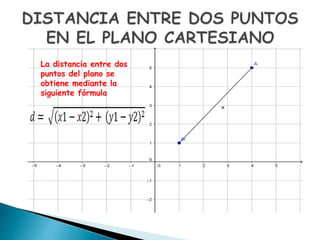
El documento discute conceptos geométricos relacionados con el plano cartesiano, incluyendo la representación de puntos, la distancia entre puntos, la pendiente de una línea recta, y la posición relativa de dos líneas rectas. También menciona a René Descartes y su establecimiento de los fundamentos de la geometría analítica y el sistema de coordenadas cartesianas.

1. Profesor José Wilson Alfaro Tapia

2. 1)Representación de un punto en el
plano cartesiano.
2) Distancia entre dos puntos en el
plano cartesiano.
3) Concepto de pendiente de una recta.
4) Discusión del valor de la pendiente
5) Posición relativa de dos líneas rectas
en el plano.

3.  Matemático, físico y
filósofo francés. Estableció
los fundamentos de la
Geometría Analítica. El
Sistema de ejes de
coordenados
perpendiculares es llamado
Sistema Cartesiano en
honor de su creador Renato
Cartesius, nombre de
Descartes en latín.
 (Álgebra y Geometría
II,Las Heras,Fuenzalida,
Lara,y Riveros, pág33,Edit.
Santillana)
holismoplanetario.files.wordpress.c
om/2015/01/descartes.jpg?w=812

4. Para determinar la
posición de un punto
en un plano se le
asocia un par
ordenado (X,Y) de
números reales, que
constituyen sus
coordenadas respecto
de un sistema de ejes
cartesianos.

5. La distancia entre dos
puntos del plano se
obtiene mediante la
siguiente fórmula

6. www.youtube.com/watch?v=28nc-L-5o9E

7. POSICIÓN RELATIVA DE DOS LÍNEAS
RECTAS EN EL PLANO.
www.youtube.com/watch?v=QY0mJGQjE5E
ECUACIÓN GENERAL Y PARTICULAR
DE LA LÍNEA RECTA
www.youtube.com/watch?v=lvAAGy2fRik

8. Representación de
un punto A(x,y)
Distancia entre dos
puntos
Pendiente de una
línea recta.
Ecuación General
Ax + By + C = 0
Ecuación Canónica
Y = mX + b