El documento presenta una introducción a la historia de la lógica. Explica que la lógica surgió en la antigua Grecia con filósofos como Platón, Aristóteles y Euclides, quienes establecieron los principios formales de las matemáticas y la lógica. Más tarde, durante la Revolución Científica, pensadores como Descartes y Newton contribuyeron al desarrollo de la ciencia matemática. Finalmente, introduce las distintas etapas en la historia de la lógica, incluyendo

1. CURSO de LOGICA UNIDAD I Conceptos Introductorios

2. CURSO de LOGICA Qué es Lógica

3. Lo mas valioso no es lo que tienen en sus vidas, si no a quién tienen en sus vidas… anónimo

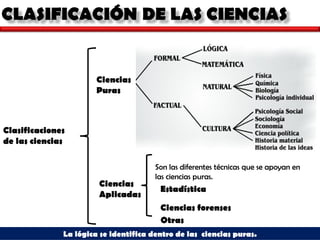
4. La Lógica es un término que deriva del griego "Λογικός" (logikê-logikós), que a su vez es "λόγος" (logos), que significa razón. [1] La Lógica es la ciencia encargada de estudiar el pensamiento a través de las Formas Mentales . Se considera que Aristóteles fue el que fundó la Lógica como un medio de conocimiento o Propedéutica , una herramienta básica para todas las Ciencias [2] . La Lógica según Immanuel Kant es una ciencia formal, es decir, aquella ciencia que estudia las formas del pensamiento prescindiendo de todo contenido. [3] Carl Sagan , en su obra El mundo y sus demonios , presenta a la razón y el uso de la lógica como un modelo de causas-efectos encadenados por una transformación, que dada la naturaleza de nuestro universo, es eminentemente termodinámica. La lógica plantea certezas y la razón busca la verdad mediante el uso de certezas descritas por la lógica material . La Lógica es ciencia de relaciones porque estudia el pensamiento y, pensar es establecer relaciones. Pero se preocupa no tanto por establecer relaciones (esto es propios de las ciencias...) sino por el estudio de las relaciones mismas, por eso la lógica es una ciencia “formal”. La lógica es una disciplina científica dirigida a satisfacer la necesidad de investigar las leyes o principios que rigen el proceso de la adquisición del conocimiento en todas sus formas, así como el modo de explicarlos. Los principios lógicos constituyen el fundamento teórico de toda indagación científica.

5. Por lo tanto, las ciencias son consideradas, en el fondo, como Lógica aplicada. Debemos recordar que el hecho lógico es anterior a la ciencia misma de la Lógica, pues la Lógica se aprende en la vida común y corriente y a eso es lo que llamamos concepto pre-científico de Lógica. ¿Qué función realiza entonces el Tratado de Lógica? Su función es vigorizar nuestras facultades mentales. En este aspecto la Lógica es muy parecida a la Gramática, la cual no nos enseña a hablar (eso lo aprendemos en la vida común y corriente), pero si nos enseña; a ser más correctos, precisos y exactos en la expresión hablada y escrita. Lo mismo sucede con las distintas operaciones lógicas que practica el hombre sin haberlas aprendido en los tratados y textos de lógica, sino en las distintas ciencias especiales que se sirven de esta y, de la experiencia cotidiana. La función de la lógica es ayudarnos a mejorar nuestro razonamiento, proporcionarnos reglas que nos ayuden a evitar falacias sofismos y paralogismos lógicos, en fin ayudarnos a evitar, errores en la forma o estructura de nuestro pensamiento. Cabe destacar que, en muchos casos, lo evidente y lo lógico son considerado lo mismo aunque lo evidente no tenga un valor absoluto para todos los tiempos ni para todos los sitios.

6. Etimológicamente hablando el término lógica procede de la voz griega “logos” que quiere decir discursos, tratado, ciencia, palabra, etc. Por eso se ha llegado a afirmar que la Lógica es la ciencia del “logos”. Es importante señalar que la traducción ordinaria de “logos” tratado, no es la principal ni la más importante a la hora de definir lo que es la Lógica; “logos” tiene varios significados; y el más clásico entre los griegos fue el de pensamiento, idea, espíritu, razón, en contraste con lo material, lo corpóreo, lo orgánico. Por lo tanto debemos afirmar que la palabra logos hace referencia al mundo de la inteligencia, del pensamiento, de la razón, de la idea ese es el campo de la Lógica. En conclusión podríamos decir que la definición nominal (o sea referente a la palabra) de Lógica es “ciencia de los pensamientos y de la razón. Científicamente hablando, la lógica es un valioso medio para ordenar conceptualmente las ideas que tenemos sobre las cosas y las relaciones que surgen de estas mismas cosas. Es este sentido, la lógica es ciencia y método a la vez. Además dentro de su rama puramente formal, la Lógica no es mas que la indagación sistemática de los principios de todo razonamiento válido.

7. CURSO de LOGICA Historia de la Lógica

8. Introducción En la filosofía moderna se critica el abuso que la escolástica medieval hizo de la lógica aristotélica. Nació así la “Lógica Informal”, o el estudio metódico de los argumentos. Durante varios siglos, sólo fue investigada por la retórica , la oratoria y la filosofía , entre otras ramas del conocimiento. Se especializó medularmente en la identificación de falacias y paradojas , así como en la construcción correcta de razonamientos. A partir de mediados del Siglo XIX la lógica formal comenzó a ser estudiada en el campo de las matemáticas y posteriormente por las ciencias computacionales, naciendo así la Lógica simbólica . La lógica simbólica trata de esquematizar los pensamientos de forma clara y sin ambigüedades. Para ello usa un lenguaje de signos propio y distinto al verbal.

9. Leibniz(fines del siglo XVIII), filósofo y matemático, pensaba que se podía crear un lenguaje simbólico tan perfecto que evitara las controversias entre los filósofos y redujera las disputas a meros errores de cálculo. Pero su obra no fue conocida en su época. En el siglo XIX, matemáticos como G. Boole y A. De Morgan intentaron expresar la forma de los razonamientos válidos en un lenguaje matemático. El desarrollo posterior de la lógica simbólica es la obra de G. Peano, C.S. Pierce, G. Frege, B. Russell y A. Whitehead, entre otros. Peano es el primero que expresa lógica matemática porque vio en la lógica un instrumento para lograr la sistematización y fundamentación de las matemáticas. Así, en la edad contemporánea, la lógica generalmente es entendida para describir razonamiento en una forma prescripta. Esto es, describe cómo el razonar debería tomar lugar. Además de encontrarle múltiples e importantes usos computacionales y matemáticos a la lógica simbólica, se ha mantenido la lógica aristotélica , la cual principalmente se ocupa de enseñar el buen argumento y es todavía enseñada, con ese designio, en la época contemporánea. Para la Lógica matemática y la filosofía analítica la lógica es un objeto de estudio en sí mismo, por lo que ésta es estudiada a un nivel más abstracto. Introducción

10. Introducción Históricamente la palabra ha ido cambiando de sentido. Comenzó siendo una modelización de los razonamientos, propuesta por los filósofos griegos, y posteriormente ha evolucionado hacia diversos sistemas formales, relacionados con la teoría. Para el estudio de la evolución de la lógica, se han tomado diversos enfoques: Por etapa Enfoque cultural El nacimiento de la lógica: Nacimiento intelectual del ser humano. La lógica emerge como mecanismo espontáneo en el enfrentamiento del hombre con la naturaleza, para comprenderla y aprovecharla.

11. China, India y Grecia entre el Siglo V y el Siglo I a.C. En China no duró mucho tiempo: la traducción y la investigación escolar en lógica fue reprimida por la dinastía Qin, acorde con la filosofía legista. En India, la lógica duró bastante más: se desarrolló (por ejemplo con la nyaya ) hasta que en el mundo islámico apareció la escuela de Asharite , la cual suprimió parte del trabajo original en lógica. (A pesar de lo anterior, hubo innovaciones escolásticas indias hasta principios del siglo XIX, pero no sobrevivió mucho dentro de la India Colonial ). El tratamiento sofisticado y formal de la lógica moderna aparentemente proviene de la tradición griega .

12. CURSO de LOGICA Historia de la Lógica Etapas

13. Clasificación de la historia de la lógica según Henri Poncairé: PRIMERO, en Tópicos : del rigor y la formalidad, a la creatividad y el caos: Etapas: Revolución Matemática. Revolución Científica. Revolución Formal. Revolución Digital. La próxima y prevista Revolución Lógica.

14. REVOLUCIÓN MATEMÁTICA Características:

15. REVOLUCIÓN MATEMÁTICA Características: Las Matem á ticas Y La L ó gica Del a ñ o 600 AC hasta 300 AC se desarrollan en Grecia los principios formales de las matem á ticas. Este periodo cl á sico lo protagonizan Plat ó n, Arist ó teles y Euclides. Plat ó n propone ideas o abstracciones. Arist ó teles resuelve el razonamiento deductivo y sistematizado. Euclides es el autor que establece el m é todo axiom á tico.

16. REVOLUCIÓN MATEMÁTICA Exponentes: Plat ó n Plat ó n, 427aC - 347 aC, propone instaurar en Siracusa una ut ó pica rep ú blica dirigida por fil ó sofos. Crea la Academia de Atenas que no era solo una instituci ó n filos ó fica, sino centro de formaci ó n pol í tica para j ó venes arist ó cratas. Seg ú n algunos especialistas, Plat ó n edifica su teor í a del conocimiento con el fin de justificar el poder emergente de la figura del fil ó sofo. Sostiene la existencia de dos mundos -el mundo de las ideas y el de mundo f í sico de los objetos. Seg ú n Plat ó n, lo concreto se percibe en funci ó n de lo abstracto y por tanto el mundo sensible existe gracias al mundo de las ideas. Plat ó n escoge el formato di á logo como forma de transmisi ó n del pensamiento.

17. REVOLUCIÓN MATEMÁTICA Exponentes: Arist ó teles Los tratados de l ó gica de Arist ó teles, 384aC - 332 aC, conocidos como Organ ó n , contienen el primer tratado sistem á tico de las leyes de pensamiento para la adquisici ó n de conocimiento. Representan el primer intento serio que funda la l ó gica como ciencia. Arist ó teles no hace de la l ó gica una disciplina metaf í sica sino que establece correspondencias rec í procas entre pensamiento l ó gico y estructura ontol ó gica. Se considera a Aristóteles ( IV a. C.) el fundador de la lógica. Para Aristóteles, la lógica era una propedéutica o introducción al saber general, pues constituye una especie de instrumento de todas las ciencias. Aristóteles fue el primero en emplear el término “Lógica” para referirse al estudio de los argumentos dentro del lenguaje natural. En el Organon Aristóteles la define como “el arte de la argumentación correcta y verdadera”.

18. REVOLUCIÓN MATEMÁTICA Exponentes: Euclides Matem á tico alejandrino autor de la universal obra, los c é lebres Elementos . Uno de los textos matem á ticos m á s relevantes de la historia del pensamiento cient í fico hasta del siglo XIX. Los Elementos est á n divididos en XIII Libros y constituyen la recopilaci ó n m á s exhaustiva de las matem á ticas conocidas en el a ñ o 300 aC. Su valor universal lo propaga el uso riguroso del m é todo deductivo que distingue entre principios -definiciones, axiomas y postulados-, y teoremas, que se demuestran a partir de los principios. A lo largo de la historia se mantuvo la sospecha de que el quinto postulado era demostrable a partir de los anteriores. El deseo de resolver tal hip ó tesis ocupa hasta el siglo XIX con la construcci ó n de las geometr í as no euclidianas y se deduce con ellas la imposibilidad de demostrar el quinto postulado.

19. REVOLUCIÓN MATEMÁTICA Exponentes: Apolonio de Perga La obra sobre curvas c ó nicas de Apolonio de Perga, « un ge ó metra de la é poca helen í stica-.

20. REVOLUCIÓN CIENTÍFICA Características: La ciencia matem á tica Ante el retroceso de la escuela cl á sica de los griegos se presentan periodos de autoridad religiosa. El Renacimiento es el inicio de una nueva revoluci ó n que revive la ciencia y las matem á ticas. Los representantes m á s destacados son Descartes, Newton y Leibniz. Este periodo abarca del a ñ o 1500dC al 1800 Dc (Siglo XV-XVIII).

21. REVOLUCIÓN CIENTÍFICA Exponentes: Ren é Descartes Fil ó sofo y matem á tico franc é s, 1596-1650 Parte de la duda universal como principio y prescinde de cualquier conocimiento previo que no quede demostrado por la evidencia con que ha de manifestarse el esp í ritu. Descartes duda de toda ense ñ anza recibida, de todo conocimiento adquirido, del testimonio de los sentidos e incluso de las verdades de orden racional. Llegado a este punto, halla una verdad de la que no puede dudar: la evidencia interior que se manifiesta en su propio sujeto ( « pienso, luego existo » ). Como cient í fico, se debe a Descartes, entre otras aportaciones de considerable importancia, la creaci ó n de la geometr í a anal í tica a la vez que aporta un corpus cuantitativo al asunto y permite el uso de m é todos algebraicos. La geometr í a exige ser cuantitativa para ser usada en ciencia e ingenier í a, y los m é todos algebraicos permiten el desarrollo m á s r á pido que los m é todos sistem á ticos -a su vez m á s rigurosos- requeridos por el enfoque axiom á tico de la geometr í a cl á sica. Ubi dubium ibi libertas , donde hay duda hay libertad.

22. REVOLUCIÓN CIENTÍFICA Exponentes: Isacc Newton A Isacc Newton , 1642-1727, Se le debe el descubrimiento de: La gravitaci ó n universal, el desarrollo del c á lculo infinitesimal, importantes descubrimientos sobre ó ptica, las leyes que rigen la mec á nica cl á sica que alimentar í a el nacimiento de la mec á nica cu á ntica. Su obra fundamental, Principios matem á ticos de la filosof í a natural (1686).

23. REVOLUCIÓN CIENTÍFICA Exponentes: Gottfried W. Leibniz Fil ó sofo y matem á tico alem á n, 1646-1716; fund ó la Academia de Ciencias de Berl í n, 1700. En Discurso sobre el arte combinatorio enuncia la necesidad de un lenguaje riguroso, exacto y universal puramente formal. Como matem á tico, su principal trabajo publicado en 1684 es la memoria Nuevo m é todo para la determinaci ó n de los m á ximos y los m í nimos , en la que expone las ideas fundamentales del c á lculo infinitesimal, anticip á ndose unos a ñ os a Newton. Introdujo el s í mbolo de integral y de diferencial de una variable. En el á rea de l ó gica matem á tica publica Generales inquisitiones de analysi notionum et veritatum y Fundamenta calculi logici .

24. REVOLUCIÓN CIENTÍFICA Exponentes: Georg Wilhelm Friedrich Hegel Fil ó sofo alem á n, 1770-1831; fascinado por la obra de Kant y de Rousseau. Autor de Ciencia de la l ó gica se le atribuye con este trabajo la constituci ó n de la l ó gica dial é ctica entendida como principio motor del concepto que disuelve y produce las particularidades de lo universal. Nikolai I. Lobachevsky Matem á tico ruso, 1792-1856; funda la Geometr í a No Euclidiana y renueva por ello los fundamentos que hasta ese momento cimentaban la ciencia de la Geometr í a. Lleva a cabo su revoluci ó n en el planteamiento que hasta entonces hab í a utilizado la ciencia Matem á tica para resolver el enigma del quinto postulado de Euclides que a su vez sirve de puerta a Lobachevsky para adentrarse en los renovados campos de lo f í sico y lo real .

25. REVOLUCIÓN FORMAL Características: Formalizaci ó n de las Matem á ticas Se caracteriza por el resurgimiento de la formalizaci ó n rigurosa de las matem á ticas, que en la etapa cl á sica griega fu é representativa. El uso de los infenitesimales fue una de las pr á cticas m á s notoria en la é poca renacentista, para la cual no se ofrec í a una justificaci ó n. La rigorizaci ó n del an á lisis lleg ó con la eliminaci ó n de los infinitesimales y la presencia de los l í mites como argumento. En este periodo se crea la l ó gica simb ó lica, la escuela formal, la l ó gica booleana, el c á lculo proposicional, la inducci ó n matem á tica. Personajes muy notables de esta etapa son: Peano, Hilbert, Frege, Boole, de Morgan, Gentzen, Russell, G ö del y Whitehead. A Rusell y G ö del se deben los planteamientos de las limitantes de la l ó gica y de la ciencia en general.

26. REVOLUCIÓN FORMAL Exponentes: Guiseppe Peano La enunciaci ó n de los principios del italiano Guiseppe Peano, 1858-1932, acerca de l ó gica matem á tica y su aplicaci ó n pr á ctica quedaron contenidos en su obra Formulaire de mathematiques . Los axiomas de Peano permiten definir el conjunto de los n ú meros naturales. David Hilbert Matem á tico alem á n, 1862-1943, aporta grandes avances a campos fundamentales de la relatividad y la mec á nica cu á ntica con la Teor í a de Invariantes y el concepto de Espacio de Hilbert . A partir de las fuentes griegas de Euclides, publica en 1899 su obra Fundamentos de Geometr í a , en la que formula sus principios de axiomatizaci ó n de la geometr í a. Seg ú n sus teor í as, es necesario establecer un conjunto de postulados b á sicos antes de plantear de modo m á s detallado cualquier tipo de problema f í sico o matem á tico.

27. REVOLUCIÓN FORMAL Exponentes: Friedrich G. Frege Junto con Boole y Peano, el matem á tico y l ó gico Friedrich G. Frege, 1848-1925, partiendo del an á lisis de los fundamentos de la matem á tica lleva a cabo la m á s profunda renovaci ó n y desarrollo de la l ó gica cl á sica hasta el momento. Es el primero en introducir los cuantificadores u operadores y en elaborar una Teor í a de la Cuantificaci ó n. George Boole El l ó gico y matem á tico George Boole, 1815-1864 Aplica el c á lculo matem á tico a la l ó gica, fundando el á lgebra de la l ó gica. El empleo de s í mbolos y reglas operatorias adecuados permite representar conceptos, ideas y razonamientos mediante variables y relaciones (ecuaciones) entre ellas. Boole dio un m é todo general para formalizar la inferencia deductiva, representando complicados raciocinios mediante sencillos sistemas de ecuaciones. Su obra principal es Investigaci ó n de las leyes del pensamiento en las que se fundan las teor í as matem á ticas de la l ó gica y la probabilidad, 1854, usadas hasta la fecha.

28. REVOLUCIÓN FORMAL Exponentes: Augustus De Morgan La mayor contribuci ó n de Augustus De Morgan (1806-1871) En el estudio de la l ó gica incluye la formulaci ó n de las Leyes de Morgan y su trabajo fundamenta la teor í a del desarrollo de las relaciones y la matem á tica simb ó lica moderna o l ó gica matem á tica. De Morgan es autor de la mayor contribuci ó n como reformador de la l ó gica. Georg F. Cantor Al matem á tico alem á n Georg F. Cantor, 1845-1918, se debe la idea del infinito continuo , es decir, la posibilidad de considerar conjuntos infinitos dados simult á neamente. Se le considera el creador de la teor í a de los n ú meros irracionales y de los conjuntos.

29. REVOLUCIÓN FORMAL Exponentes: Gentzen El alem á n Gentzen (1909-1945) formul ó la prueba de la consistencia de un sistema de aritm é tica cl á sica en el cual el m é todo no elemental es una extensi ó n de inducci ó n matem á tica a partir de una secuencia de n ú meros naturales a un cierto segmento de n ú meros ordinales transfinitos. Bertrand Rusell Bertrand Rusell (1872-1970) es uno de los creadores de la log í stica y uno de los pensadores de mayor influencia en la filosof í a cient í fica contempor á nea. Conociendo los trabajos de Cantor descubre en la Teor í a de Conjuntos varias paradojas que resuelve mediante la Teor í a de los Tipos. Establece la teor í a de la jerarqu í a de los lenguajes- para eliminar las paradojas sem á nticas. Siguiendo adem á s de los trabajos de Cantor, a Peano y Frege, Rusell se propone fundamentar y axiomatizar la matem á tica a partir de conceptos l ó gicos. Este empe ñ o culmina con la publicaci ó n (1910-1913) de los monumentales Principia Mathematica -en colaboraci ó n con Whitehead-, obra que, adem á s, sienta las bases de la moderna l ó gica formal.

30. REVOLUCIÓN FORMAL Exponentes: Kurt G ö del Kurt G ö del (1906-1978) aporta m ú ltiples contribuciones a la l ó gica matem á tica, destacando la demostraci ó n de la consistencia de la hip ó tesis cantoriana del continuo y el teorema y prueba de incompletez sem á ntica . En Sobre las proposiciones indecidibles de los sistemas de matem á tica formal establece que es imposible construir un sistema de c á lculo l ó gico suficientemente rico en el que todos sus teoremas y enunciados sean decidibles dentro del sistema. Con este teorema se demostr ó hay enunciados que no son demostrables ni refutables. Para probar esta aserci ó n se sirvi ó de la matematizaci ó n de la sintaxis l ó gica.

31. REVOLUCIÓN DIGITAL Características:

32. REVOLUCIÓN DIGITAL Exponentes: Alan Turing Matem á tico y L ó gico pionero en Teor í a de la Computaci ó n que contribuye a importantes an á lisis l ó gicos de los procesos computacionales. Las especificaciones para la computadora abstracta que é l idea -conocida como M á quina de Turing -, resulta ser una de sus m á s importantes contribuciones a la Teor í a de la Computaci ó n. Prueba que es posible construir una m á quina universal con una programaci ó n adecuada capaz de hacer el trabajo de cualquier m á quina dise ñ ada para resolver problemas espec í ficos. La M á quina de Turing es un intento para determinar si la matem á tica se puede reducir a alg ú n tipo simple de computaci ó n. Su objetivo fu é desarrollar la m á quina m á s simple posible capaz de realizar computaci ó n. La m á quina propuesta por Turing es un dispositivo relativamente simple, pero capaz de realizar cualquier operaci ó n matem á tica. Turing se ilusion ó con la idea de que su m á quina pod í a realizar cualquier proceso del cerebro humano, inclusive la capacidad de producir conciencia de uno mismo.

33. REVOLUCIÓN DIGITAL Exponentes: Norbert Weiner El cient í fico norteam é ricano Norbert Weiner (1894-1964) en 1947 publica su libro m á s famoso: Cibern é tica, o control y comunicaci ó n en el animal y la m á quina ; en donde se utiliza por primera vez la palabra Cibern é tica. Existen muchas definiciones de Cibern é tica -del griego kybernetes , piloto-, y Norbert Weiner da vida a la palabra con una definici ó n simple: La Cibern é tica es la ciencia que estudia la traducci ó n de procesos biol ó gicos a procesos que reproduce una m á quina . Desde los inicios la Cibern é tica se relaciona directamente con ciencias como Neurolog í a, Biolog í a, Biosociolog í a , Rob ó tica e Inteligencia Artificial.

34. REVOLUCIÓN DIGITAL Exponentes: Luitzen Egbertus Jan Brouwer Matem á tico y l ó gico alem á n (1881-1966) conocido como LEJ Brouwer y fundador de la escuela de la L ó gica intuicionista Son significativos sus trabajos Life, Art and Mysticism (1905) y Sobre la infiabilidad de los principios l ó gicos . Alfred Tarski Matem á tico y l ó gico y fil ó sofo polaco (1902-1983). Em é rito profesor de la University of California, Berkeley, Realiza importantes estudios sobre á lgebra en general, teor í a de mediciones, l ó gica matem á tica, teor í a de conjuntos, y metamatem á ticas. El trabajo de Tarski 5 incluye respuestas a la paradoja de Banach-Tarski , el teorema de la indefinibilidad de la verdad, las nociones de cardinal, ordinal, relaci ó n y es inductor de las á lgebras cil í ndricas.

35. REVOLUCIÓN DIGITAL Exponentes: Benoit Mandelbrot El gran impulsor de la matem á tica contempor á nea y pionero de la geometr í a fractal 6 a quien la computaci ó n pura revela la moderna Geometr í a de la Naturaleza . Fractal y geometr í a fractal son el corpus principal de sus investigaciones adem á s de los sistemas irreversibles.

36. LA PRÓXIMA Y PREVISTA REVOLUCIÓN LÓGICA. Características: La siguiente Revoluci ó n L ó gica incorpora la fusi ó n entre matem á ticas y computaci ó n. Las computadoras tienden a explorar datos inteligentemente transfiriendo informaci ó n de las bases de datos a las bases de conocimiento interconectadas a trav é s de la Red a escala infinitesimal. La l ó gica evoluciona pues como un gen hacia la culminaci ó n del conocimiento libre que nace del rigor formal de la Matem á tica griega; emerge renovadamente de etapas de persecuci ó n tan oscuras como la Edad Media y otros intentos m á s recientes; hasta el intercambio constante y continuo de datos en la moderna era de estructura de redes que Internet proporciona a modo neuronal a la Humanidad.

38. Mientra vivas Levanta tu mirada al cielo y acuerdate de tu creador, valora el don maravilloso de la vida y atrevete a ser feliz con lo que Dios te ha dado, recuerda que cada dia es un Presente que debemos aprovecharal maximo y que los momentos dificiles son oportunidades para fortalecernos. Y si hoy aparece obscuro tu cielo no olvides que mañana el SOL BRILLARA PARA TI ......

40. CURSO de LOGICA

41. Clasificaciones de las ciencias Ciencias Aplicadas La lógica se identifica dentro de las ciencias puras. Otras Ciencias Puras Son las diferentes técnicas que se apoyan en las ciencias puras. Estadística Ciencias forenses

42. Aplicada a las ciencias Aplicada a los procesos Aplicada a las matemáticas Trabajar en grupo y hacer un ensayo sobre la aplicación de la Lógica.

43. Aplicada a las ciencias Se relaciona con todas las ciencias. Todo las ciencias porque todas ellas trabajan sobre diversos lenguajes simbólicos Todas establecen relaciones de pensamiento entre varias ideas. Lógica es una ciencia de relaciones y (sobre todo) la ciencia que estudia las relaciones, OBJETO FORMAL Y OBJETO MATERIAL El objeto formal caracteriza a una ciencia y el objeto material estrecha relaciones entre dos o más ciencias. La Lógica tiene relación con todas las ciencias pero tiene una relación especial con algunas de ellas. Todas las ciencias poseen un objeto formal distinto a las otras, esta particularidad es como la huella digital que los identifica. A través del objeto formal podemos identificar y distinguir las disciplinas del saber aunque posean ciertas similitudes. El objeto material por su parte puede ser compartido por varias ciencias. Un claro ejemplo de esto lo representan la Lógica, la Gramática, la Teoría del Conocimiento y la Psicología las cuales poseen el mismo objeto material: el pensamiento .

44. … Aplicada a las ciencias La lógica estudia los problemas del movimiento del hombre hacia el conocimiento certero. Para la lógica lo central es aclarar qué es una certeza y cómo se alcanza. La lógica no entra en definir qué es verdad y qué es mentira. Esos conceptos, al tener cierta carga moral, son competencia del razonamiento. Por tanto, la ciencia no define qué es verdad o mentira: define certezas. Estas últimas, son indispensables para todas las ciencias. La filosofía es la disciplina que se encarga de enseñar a elaborar y proponer metodologías de cómo falsar las certezas firmes, a través de los razonamientos: ya sean deductivos, inductivos ó abductivos.

45. Aplicada a los procesos La lógica es el "proceso de reflejo del mundo objetivo en la conciencia del hombre y de verificación de la corrección de este reflejo por la práctica, es generada históricamente por la vida de los hombres concretos, cuando se separan de los fenómenos de la naturaleza “ CONOCIMIENTO CIENCIAS SISTEMAS Sub Sistemas Procesos Acciones

46. Aplicada a las matemáticas El hombre de hoy se relaciona más frecuentemente con la lógica matemática que se refiere a un sistema deductivo en el que existen ciertos axiomas básicos y ciertas reglas de deducción. Ese sistema está formado por un conjunto de expresiones (o símbolos) que permiten construir determinadas proposiciones (o secuencias de signos dotables de significado), las reglas deductivas permiten reconocer cuales son las afirmaciones deducibles de los axiomas mediante las reglas de deducción y cuáles no. Matematización de la lógica. Primero inicia la lógica formal, desde los tiempos de Aristóteles.. Esto se da a mediados del siglo XIX; a través de los lenguajes simbólicos. La clave de los cambios se encuentra en Boole y Frege, autores de lo conocido como matematización de la lógica . Con este término se entiende la subordinación de una ciencia al método de las matemáticas.