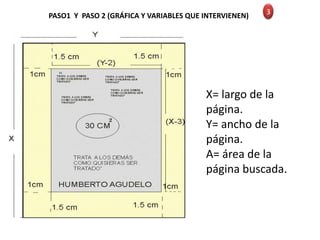
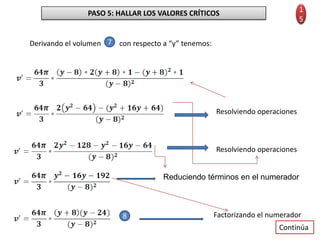
El documento presenta 5 problemas relacionados con máximos y mínimos. El primer problema busca las dimensiones de una página que minimicen el área total usando el papel, dado un área impresa fija. El segundo problema busca las dimensiones de un cilindro que minimicen el área total de la lámina usada, dado un volumen fijo de 125 cm3. El tercer problema busca las dimensiones de un cono circular que minimice el volumen al circunscribirse en una esfera de radio 8 cm.

1. 1PROBLEMAS DE APLICACIÓN SOBRE MÁXIMOS Y MÍNIMOS

2. 2PROBLEMA 1Las márgenes superior e inferior de una página son ambas 1.5 cm y las márgenes laterales son de 1 cm cada una. Si el área del material impreso por página es fijo e igual a ¿cuáles deben ser las dimensiones de la página de modo que la cantidad de papel a emplear fuera mínima?

3. 3PASO1 Y PASO 2 (GRÁFICA Y VARIABLES QUE INTERVIENEN)X= largo de la página.Y= ancho de la página.A= área de la página buscada.

4. 4PASO 3 Y PASO 4: ÁREA A MINIMIZAR EXPRESADA EN UNA SÓLA VARIABLE.

5. 5PASO 5: HALLAR LOS VALORES CRÍTICOS

6. 6PASO 6:DECIDIR SI EL MÍNIMO HALLADO TIENE LUGAR EN PROBLEMAHUMBERTO AGUDELO ZAPATA

7. 7PROBLEMA 2Se quiere construir un envase cilíndrico de base circular cuyo volumen sea 125 cm3. Hallar las dimensiones que debe tener para que la cantidad de lámina empleada (área total) sea mínima.

8. 8PASO1 Y PASO 2 (GRÁFICA Y VARIABLES QUE INTERVIENEN)r = radio de los círculosh= altura del cilindro

9. PASO 3 Y PASO 4: ÁREA A MINIMIZAR EXPRESADA EN UNA SÓLA VARIABLE.9El área a minimizar en este caso, es el área de la lámina que se va a gastar, las dos tapas (área de dos círculos) y el área que envuelve al cilindro (un rectángulo de altura h y de largo 2πrh.A=Sabemos que el volumen de cilindro de tener 125 cm3Y la ecuación de volumen de un cilindro es Por lo tanto, ÁREA A MINIMIZAR

10. 10PASO 5: HALLAR LOS VALORES CRÍTICOS Para hallar la menor cantidad de material empleado derivamos a A con respecto a r:Los valores críticos de A se obtienen cuando A’=0 o cuando A’ no existe; es decir cuando: ÓDe estos valores críticos descartamos de una vez a (no existen radios =0).

11. 11PASO 6:DECIDIR SI EL MÍNIMO HALLADO TIENE LUGAR EN PROBLEMAFinalmente comprobamos que es un valor mínimo calculando A’’ y verificando que A’’Este valor dadas las condiciones será positivo.Calculando la A’’ se tiene El valor de h lo obtenemos reemplazando el valor de r en la ecuación de volumen de un cilindro Luego las dimensiones del cilindro deben ser :cmcm

12. 12PROBLEMA 3Hallar las dimensiones de un cono circular recto de volumen mínimo que se puede circunscribir en una esfera de 8 cm de radio.

13. 13PASO1 Y PASO 2 (GRÁFICA Y VARIABLES QUE INTERVIENEN)Como los triángulos rectángulos AED son semejantes , entonces podemos establecer proporcionalidad entre sus lados correspondientes; así:1

14. PASO 3 Y PASO 4: VOLUMEN A MINIMIZAR EXPRESADA EN UNA SÓLA VARIABLE.14Continuación…Elevando al cuadrado ambos miembros de la ecuación 1Factorizando el miembro derechoSimplificando24Ahora bien, el volumen de un cono es: Donde35Sustituyendo y en 4536Sustituyendo en 26Esta es la función de volumen a minimizar7

15. 15PASO 5: HALLAR LOS VALORES CRÍTICOS Derivando el volumen con respecto a “y” tenemos:7Resolviendo operacionesResolviendo operacionesReduciendo términos en el numerador Factorizando el numerador8Continúa

16. 16Los valores críticos de A se obtienen cuando A’=0 o cuando A’ no existe; es decir cuando:óLuego los valores críticos son:Analizando estos valores encontramos que y =-8 y y =8 deben descartarse (y =-8 por ser negativo y y = 8 es un absurdo dentro del contexto del problema).

17. 17PASO 6:DECIDIR SI EL MÍNIMO HALLADO TIENE LUGAR EN PROBLEMADerivando por segunda vez el volumen, tenemos Hallando la segunda derivada de v podemos comprobar que y = 24 es un valor mínimo.Obsérvese que se sustituimos y=24 en v’’ el resultado será v’’> 0Finalmente, tomando como valor y =24 , encontramos que: HUMBERTO AGUDELO ZAPATA

18. 18PROBLEMAS PROPUESTOS SOBRE MÁXIMOS Y MÍNIMOS SEGUNDA PARTEPROBLEMA 1Una caja rectangular de base cuadrada se construye de tal manera que el área de sus seis caras es . ¿Cuáles son las dimensiones de la caja que hacen que su volumen Sea máximo?. PROBLEMA 2Un cono circular recto tiene un volumen de . ¿cuáles deben ser sus dimensiones para que su área lateral sea mínima. Una ventana tiene forma de rectángulo coronado por un semicírculo. Hallar sus dimensiones cuando el perímetro es de y el área es la mayor posible. PROBLEMA 3PROBLEMA 4Hallar las dimensiones del cilindro de mayor área lateral que se puede Inscribir en una esfera de radio . PROBLEMA 5Un terreno rectangular va ha ser cercado. El material que se necesita Para para dos de sus lados paralelos cuesta $ 120 por cada metrolineal. Los otros dos lados paralelos serán cercados con un material quecuesta $ 200 por metro lineal. ¿Hallar las dimensiones del terreno demayor área posible que puede ser cercado con un costo de $ 18000?

19. 19RESUELVA LOS EJERCICIOS SINO LOS HA REALIZADO, ES POR SU BIEN.