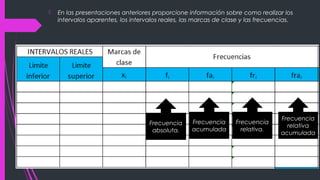
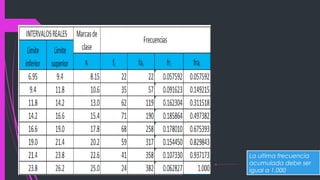
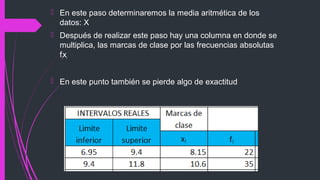
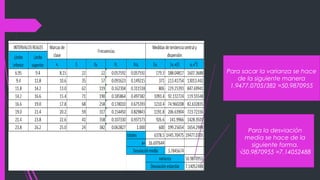
Este documento proporciona instrucciones para calcular medidas de tendencia central y dispersión a partir de datos de frecuencias absolutas. Explica cómo calcular la media aritmética, desviación media, varianza y desviación estándar mediante la suma de productos de las marcas de clase y las frecuencias absolutas. También muestra los pasos para hallar cada medida de forma precisa.

1. Diana Laura Ochoa Gallegos
3°B
Lic. Edgar Mata Ortiz.

2.  este ultimo paso consiste en , calcular
algunas medidas de tendencia central y
dispersión:
 Media aritmética.
 Desviación media.
 Varianza
 Desviación estándar

3.  En las presentaciones anteriores proporcione información sobre como realizar los
intervalos aparentes, los intervalos reales, las marcas de clase y las frecuencias.
Frecuencia
absoluta.
Frecuencia
acumulada
Frecuencia
relativa.
Frecuencia
relativa
acumulada

4. La ultima frecuencia
acumulada debe ser
igual a 1.000

5.  En este paso determinaremos la media aritmética de los
datos: X
 Después de realizar este paso hay una columna en donde se
multiplica, las marcas de clase por las frecuencias absolutas
fixi
 En este punto también se pierde algo de exactitud

6. La tabla queda de esta forma cuando ya hemos
sacado la multiplicación de fixi
Recuerden solo se
multiplicara
8.15*22=179.3
Y así sucesivamente
Luego sacaremos la
sumatoria para así
obtener la media
aritmética
Luego sacaremos la
sumatoria para así
obtener la media
aritmética
La media aritmética se
obtiene de la siguiente
manera
6.378.5/382=16.697644
La media aritmética se
obtiene de la siguiente
manera
6.378.5/382=16.697644
La media aritmética nos indica el punto medio de los
datos, es una medida de tendencia central
La media aritmética nos indica el punto medio de los
datos, es una medida de tendencia central

7.  Siguiente paso determinar la desviación media de los datos:
Dx
 La desviación media es el promedio de las distancias de cada
dato, respecto a la media.
 La formula es la siguiente:
 |xi- x| fi = Diferencia absoluta entre cada marca de clase y
la media por la frecuencia absoluta.
Bueno para que el resultado sea exacto se
realizara de esta manera
8.15 -16.697644= +8.547644 (22)
=188.04
Y así sucesivamente.
Nota: Los resultados salen negativos, pero
debemos ponerlos positivos.
Bueno para que el resultado sea exacto se
realizara de esta manera
8.15 -16.697644= +8.547644 (22)
=188.04
Y así sucesivamente.
Nota: Los resultados salen negativos, pero
debemos ponerlos positivos.

8. Aquí ya vemos
como quedaron
todos losvalores.
Veamos como nos quedan los
valores.
La sumatoria de los
valores.
Para sacar la desviación
media
1445.70475/382 =3.7845674

9.  En este paso determinaremos la varianza y la desviación
estándar de los datos: s2
y S
 La formula es la siguiente:
 Xi – x2
fi = el cuadrado de la diferencia de cada marca de clase y la media por la frecuencia absoluta.
Para calcularlos de la forma correcta
se hace de la siguiente manera:
(8.15-16.697644)2
=73.06221795 * 22
=1607.368795
Y así sucesivamente con cada uno
veamos como queda en la tabla que
les mostrare…..

10. Para sacar la varianza se hace
de la siguiente manera
1.9477.0705/382 =50.9870955
Para la desviación
media se hace de la
siguiente forma.
√50.9870955 =7.14052488