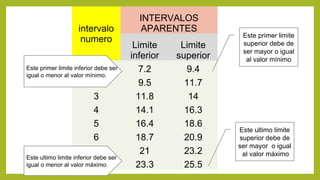
Este documento describe los pasos para construir intervalos aparentes para un conjunto de datos que tienen un valor máximo de 25.8 y un valor mínimo de 7.3, usando 8 intervalos. Después de probar varios casos con diferentes tamaños de intervalo, se obtiene la solución óptima con un tamaño de intervalo de 2.4, donde los intervalos cumplen con todas las condiciones requeridas.

1. Diana Laura Ochoa Gallegos
3°B
Lic. Edgar Mata Ortiz.

2. MAX 25.8
MIN 7.3
RANGO 18.5
el valor máximo y
el valor mínimo
los sacaremos de
un grupo de
datos.
Para sacar el
rango se resta el
valor máximo y elmínimo
DATOS

3. # de intervalos 8
Tamaño del intervalo. 2.3125
tam.de
interv.redondeado 2.3
Para determinar el
tamaño de intervalos
se divide el rango
entre el # de
intervalos.
18.5/8=2.3125
En este caso vamos a tomar como
tamaño de intervalo redondeado 2.3 si
los datos fueran enteros lo tomaríamos
como un entero por ejemplo 3 o 4. pero
en este caso deben de ser decímales
podemos tomar 2.3 , 2.4 o 2.52.3 , 2.4 o 2.5 en este
primer caso tomaremos 2.3 y veamos
como queda.

4. • Después pasamos a construir los 8 intervalos aparentes.
intervalo numero
INTERVALOS APARENTES
Limite inferior Limite superior
1 7.2
2
3
4
5
6
7
8
El valor inicial debe de ser menor o igual
al mínimo, en este caso utilizamos el 7.2
que es igual al mínimo. Este también
puede cambiarse en caso de que le sea
necesario
CASO 1

5. intervalo numero
INTERVALOS APARENTES
Limite inferior Limite superior
1 7.2
2 9.5
3 11.8
4 14.1
5 16.4
6 18.7
7 21
8 23.3
Para poder sacar los
otros limites inferiores
le vamos a ir
sumando el tamaño
de intervalo
redondeado que en
este caso es 2.3 y
queda de esta forma.
+
+
+
+
7.2+2.3=9.5
9.5+2.3=11.8
Y así
sucesivamente
hasta llegar a los
8 intervalos

6. intervalo
numero
INTERVALOS
APARENTES
Limite
inferior
Limite
superior
1 7.2
2 9.5
3 11.8
4 14.1
5 16.4
6 18.7
7 21
8 23.3
MAX 25.8
MIN 7.3
RANGO 18.5
Cuando hayamos terminado todos los
limites inferiores debemos de revisar
que el ultimo limite sea igual o menor al
valor máximo.
En este caso nos podemos
dar cuenta que si cumple.

7. intervalo
numero
INTERVALOS
APARENTES
Limite
inferior
Limite
superior
1 7.2 9.4
2 9.5 11.7
3 11.8 14
4 14.1 16.3
5 16.4 18.6
6 18.7 20.9
7 21 23.2
8 23.3 25.5
ya que obtuvimos los limites inferiores ahora
tenemos que sacar los LIMITES
SUPERIORES. Estos se sacan de la
siguiente manera bueno para obtener el
primer limite se hace de esta manera.
9.5-.1=9.4
Nota: le restamos .1 porque estamos hablando
de decimales si fueran enteros pues seria 1.
Para el segundo limite y los que faltan les
sumaremos 2.3.
9.4+2.3= 11.7
11.7+2.3=14
Y así sucesivamente hasta llegar a los 8
intervalos

8. intervalo
numero
INTERVALOS
APARENTES
Limite
inferior
Limite
superior
1 7.2 9.4
2 9.5 11.7
3 11.8 14
4 14.1 16.3
5 16.4 18.6
6 18.7 20.9
7 21 23.2
8 23.3 25.5
Este primer limite inferior debe ser
igual o menor al valor mínimo.
Este ultimo limite inferior debe ser
igual o menor al valor máximo.
Este primer limite
superior debe de
ser mayor o igual
al valor mínimo
Este ultimo limite
superior debe de
ser mayor o igual
al valor máximo

9. Bueno como podemos darnos cuenta no se cumplió una de las
condiciones, debido a que el ultimo limite superior debe de ser igual o
mayor al valor máximo. Lo que podemos hacer es lo siguiente:
◘Cambiar el primer límite inferior.
◘ Cambiar el tamaño del intervalo.
◘Cambiar el numero de intervalos.
Ya ajustados estos valores trataremos de cumplir con las cuatro
condiciones de modo que los intervalos sigan siendo 8.
Es casi imposible que ningún método resulte, y así tengamos que usar
el ultimo punto que es imposible que suceda pero en algunos casos si
sucede.
interval
o
numero
INTERVALOS
APARENTES
Límite
inferior
Límite
superio
r
1 7.2 9.4
2 9.5 11.7
3 11.8 14
4 14.1 16.3
5 16.4 18.6
6 18.7 20.9
7 21 23.2
8 23.3 25.5
Este ultimo límite
superior debe de
ser mayor o igual
al valor máximo

10. Bueno para poder ajustar nuestros datos vamos a cambiar el tamaño
del intervalo el siguiente es el que se utilizo en el primer caso.
Tamaño del intervalo = 2.3125
tam.de intervalo redondeado = 2.3
Bueno el tamaño de intervalo puede ser redondeado a
2.4 o 2.5
En este segundo caso vamos a utilizar el 2.5 como nuevo
tamaño de intervalo redondeado y veamos que resultados
obtenemos.
CASO 2

11. Tamaño de intervalo
redondeado = 2.5
intervalo
numero
INTERVALOS
APARENTES
Limite
inferior
Limite
superior
1 7.2 9.6
2 9.7 12.1
3 12.2 14.6
4 14.7 17.1
5 17.2 19.6
6 19.7 22.1
7 22.2 24.6
8 24.7 27.1
Este primer limite
inferior debe ser
igual o menor al
valor mínimo.
Este ultimo limite inferior
debe ser igual o menor al
valor máximo.
Este primer
limite superior
debe de ser
mayor o igual al
valor mínimo
Este ultimo
limite superior
debe de ser
mayor o igual
al valor máximo
Como podemos
darnos cuenta
estos valores si
cumplen con las
cuatro
condiciones
pero podemos
mejorarlo
veamos como.

12. Lo primero que aremos para mejorar los valores es que, vamos a mejorar el valor inicial.
7.3 - 7.2= 0.1
recuerden que el 7.3 es el valor mínimo que debemos de tomar y el 7.2 es porque podemos
elegir como primer limite inferior un número igual o menor al valor mínimo.
27.1 - 25.8=1.3
El 27.1 es el ultimo límite superior y el 25.8 es el primer límite superior.
La mitad de 1.3 es .65 tomaremos .6 y quedara de la siguiente manera:
7.2 - .6= 6.6
Nuestro primer limite inferior será 6.6 veamos como quedan los valores de la tabla y veamos
si cumplen con las cuatro condiciones.
Tamaño de intervalo
redondeado =2.5
Caso 3

13. intervalo
numero
INTERVALOS
APARENTES
Limite
inferior
Limite
superior
1 6.6 9
2 9.1 11.5
3 11.6 14
4 14.1 16.5
5 16.6 19
6 19.1 21.5
7 21.6 24
8 24.1 26.5
Este primer limite
inferior debe ser
igual o menor al
valor mínimo.
Este ultimo limite inferior
debe ser igual o menor al
valor máximo.
Este primer
limite superior
debe de ser
mayor o igual al
valor mínimo
Este ultimo
limite superior
debe de ser
mayor o igual
al valor máximo
Como podemos
darnos cuenta
estos valores
también cumplen
con las cuatro
condiciones pero
aun podemos
mejorarlo veamos
otro caso

14. Bueno como pudimos darnos cuenta en los caso
anteriores los valores si cumplían pero lo que queremos
lograr es que los valores sean más precisos a lo que nos
pide.
Como ya les había mencionado podemos redondear el
tamaño de intervalo y es lo que aremos nuevamente en
este caso
El tamaño de intervalo redondeado será de : 2.4
Y veamos que resultados obtenemos
Caso 4

15. intervalo
numero
INTERVALOS
APARENTES
Limite
inferior
Limite
superior
1 7.2 9.5
2 9.6 11.9
3 12 14.3
4 14.4 16.7
5 16.8 19.1
6 19.2 21.5
7 21.6 23.9
8 24 26.3
En este caso también
vemos como si cumple
con las cuatro condiciones
pero nosotros lo que
queremos es que los
valores de nuestra tabla
sean lo mas cercano a
nuestros valores máximo
y mínimo.
Así que veamos el ultimo
caso y veamos que
sucede.
Este primer limite
inferior debe ser
igual o menor al
valor mínimo.
Este ultimo limite
inferior debe ser igual
o menor al valor
máximo.
Este primer
limite superior
debe de ser
mayor o igual al
valor mínimo
Este ultimo
limite superior
debe de ser
mayor o igual
al valor máximo

16. Lo primero que aremos para mejorar los valores es que, vamos a mejorar el valor inicial.
7.3 - 7.2= 0.1
recuerden que el 7.3 es el valor mínimo que debemos de tomar y el 7.2 es porque podemos
elegir como primer limite inferior un número igual o menor al valor mínimo.
26.3 - 25.8=.5
El 26.3 es el ultimo límite superior y el 25.8 es el primer límite superior.
La mitad de .5 es .25 tomaremos .2 y quedara de la siguiente manera:
7.2 - .2= 7.0
Nuestro primer limite inferior será 7.0 veamos como quedan los valores de la tabla y veamos
si cumplen con las cuatro condiciones.
Caso 5
Tamaño de intervalo
redondeado = 2.4

17. Tamaño de
intervalo
redondeado = 2.4
intervalo
número
INTERVALOS
APARENTES
Limite
inferior
Limite
superior
1 7.0 9.3
2 9.4 11.7
3 11.8 14.1
4 14.2 16.5
5 16.6 18.9
6 19 21.3
7 21.4 23.7
8 23.8 26.1
Este primer limite
inferior debe ser
igual o menor al
valor mínimo.
Este ultimo limite
inferior debe ser igual
o menor al valor
máximo.
Este primer
limite superior
debe de ser
mayor o igual al
valor mínimo
Este ultimo
limite superior
debe de ser
mayor o igual
al valor máximo
Como podemos
darnos cuenta este
caso es el que
cumple con las 4
condiciones que
deseamos por lo
tano esta seria la
solución optima ya
que es el más
adecuado, para este
problema

18. ◘Finalmente hemos obtenido los intervalos aparentes
son necesarios para cuando tenemos que contar los
datos manualmente así que pueden hacerlo y ponerlo
aparte en realidad los que deben anotarse en la tabla
son los intervalos reales
◘En la siguiente presentación que les proporcionare
podremos ver la explicación de como realizar los
intervalos reales.