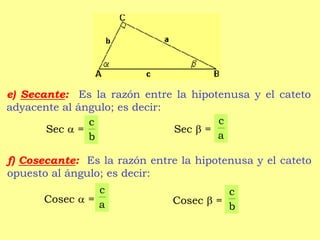
El documento presenta los conceptos básicos de la trigonometría en triángulos rectángulos, incluyendo las definiciones de seno, coseno, tangente y otras funciones trigonométricas, así como fórmulas y valores para ángulos de 30°, 45° y 60°. También incluye ejemplos de cálculos trigonométricos y la resolución de problemas geométricos usando estas relaciones.

1. Trigonometría en el triángulo :
 Definición de seno, coseno, tangente, cotangente,
secante y cosecante en el triángulo rectángulo.
 Algunas formulas entre razones trigonométricas.
 Razones trigonométricas de 30º, 45º y 60º.
 Ángulos de elevación y depresión.
 Problemas de planteo en función de calcular alturas
o distancias aplicando razones trigonométricas.

2. Razones trigonométricas en el triángulo rectángulo:
En el triángulo rectángulo se establece una serie de
relaciones entre sus lados y ángulos agudos; relaciones
que reciben el nombre de razones trigonométricas, las
que son seis y a continuación se definen:

3. a) Seno: Es la razón entre el cateto opuesto al ángulo
agudo y la hipotenusa; es decir:
Sen  = Sen  =
b) Coseno: Es la razón entre el cateto adyacente al
ángulo agudo y la hipotenusa; es decir:
Cos  = Cos  =
c
a
c
b
c
b
c
a

4. c) Tangente: Es la razón entre el cateto opuesto al
ángulo agudo y el cateto adyacente a este; es decir:
Tg  = Tg  =
d) Cotangente: Es la razón entre el cateto adyacente al
ángulo agudo y el cateto opuesto a este; es decir:
Cotg  = Cotg  =
b
a
a
b
a
b
b
a

5. e) Secante: Es la razón entre la hipotenusa y el cateto
adyacente al ángulo; es decir:
Sec  = Sec  =
f) Cosecante: Es la razón entre la hipotenusa y el cateto
opuesto al ángulo; es decir:
Cosec  = Cosec  =
a
c
b
c
a
c
b
c

6. Notar que:
Cada función trigonométrica tiene una cofunción; así
seno y coseno, tangente y cotangente, secante y
cosecante son cofunciones; además como  y  son
complementarios; se deduce que:
"la función trigonométrica de un ángulo agudo es
igual a la cofunción de su complemento".

7. Ejercicios:
1) Determine el valor de las funciones trigonométricas de
los ángulos agudos en cada uno de los siguientes
triángulos rectángulos.
Sen  =
x
x2 = 52 + 122
x2 = 25 + 144 = 169
169
2
x 
x = 13
=13
13
12
Cos  =
13
5
Tg  =
5
12
Cotg  =
12
5
Sec  =
5
13
Cosec  =
12
13
Sen  =
13
5
Cos  =
13
12
Tg  =
12
5
Cotg  =
5
12
Sec  =
12
13
Cosec  =
5
13

8. x
2
)
5
3
(
2
6
2
x 

x2 + 36 = 45
x2 = 45 - 36 = 9
9
2
x 
x = 3
Sen  =
Cos  =
Tg  =
5
5
2
25
5
2
5
5
5
2
5
3
6





5
5
25
5
5
5
5
1
5
3
3





=3
1
1
2
3
6

Cotg  =
2
1
6
3

Sec  =
Cosec  =
5
3
5
3

1
1
2
5
6
5
3

1
2

9. Sen  =
Cos  =
Tg  =
Cotg  =
Sec  =
Cosec  =
5
5
2
5
5
2
2
1
5
2
5
Sen  =
Cos  =
Tg  =
Cotg  =
Sec  =
Cosec  =
5
5
2
5
5
2
2
1
5
2
5
"la función trigonométrica de un ángulo agudo es
igual a la cofunción de su complemento".

10. 2) A partir del valor de las funciones trigonométricas
dadas, obtener el valor de las funciones trigonométricas
restantes:
(a) Si Sen  = 0,6
Asociando los valores como
medidas de los lados de un
rectángulo:
5
3
10
6

 Cateto opuesto
hipotenusa
3
5
x=4
Cos  =
5
4
Tg  =
4
3
Cotg  =
3
4
Sec  =
4
5
Cosec  =
3
5

11. b) Si tg  =
3
3
2 Cat. Op.
Cat.ady.
Asociando los valores como
medidas de los lados de un
rectángulo:
3
x
3
2
2
)
3
2
(
2
3
2
x 

x2 = 9 + 12 = 21
21
2
x 
21
x 
21

Sen  =
Cos  =
Cotg  =
7
7
2
21
7
3
2
21
63
2
21
21
21
3
2
21
3
2







7
21
21
21
3
21
21
21
3
21
3




2
3
3
2
3
3
3
3
2
3
3
3
2
3





1
7
1
7
1
1

12. Sec  =
Cosec  =
3
21
2
7
3
2
7
3
9
2
63
3
3
2
3
21
3
2
21







1
1
El hecho de asociar medidas a los lados de un
rectángulo; no significa que estas sean las únicas
medidas de tales lados, ya que hay muchos números en
una determinada razón.

13. Algunas formulas:
1
2
Cos
2
Sen
)
1 






 2
Cos
1
2
Sen



 2
Sen
1
2
Cos



 2
Cos
1
Sen



 2
Sen
1
Cos

1
sec
Co
Sen
)
2 






sec
Co
1
Sen



Sen
1
sec
Co


14. 1
Sec
Cos
)
3 






Sec
1
Cos



Cos
1
Sec

1
tg
Co
Tg
)
4 


 



tg
Co
1
Tg



Tg
1
tg
Co




Cos
Sen
Tg
)
5




Sen
Cos
tg
Co

15. Verifiquemos algunas de estas igualdades en el triángulo
rectángulo:
(a) Sen2  + cos2  = 1
c
a
Sen 

2
c
2
a
2
Sen 

c
b
Cos 

2
c
2
b
2
Cos 




 2
Cos
2
Sen 



2
c
2
b
2
a
2
c
2
b
2
c
2
a
1
2
c
2
c

/2 /2

16. (b) Sen  . Cosec  = 1
Sen  =
Cosec  =
c
a
a
c
Sen  · Cosec  = 

a
c
c
a
1
1
1 1
1
1
1





Cos
Sen
Tg
)
c
(
b
a
b
c
c
a
c
b
c
a
Cos
Sen






b
a
Tg 





Cos
Sen
Tg

1
1

17. Funciones trigonométricas de 30º 45º y 60º.
a) De 45º: Se construye un triángulo rectángulo
isósceles de catetos de medida igual a la unidad:
x
x2 = 12 + 12
x2 = 1 + 1 = 2
2
2
x 
2
x 
2

Sen 45º =
Cos 45º =
Tg 45º =
Cotg 45º =
Sec 45º =
Cosec 45º =
2
2
2
2
2
1
2
1



 1
1
1

2
1
2

2
1
2

1
1
1

2
2
2
2
2
1
2
1





18. b) De 30º y 60º: Se construye un triángulo equilátero
lado 2 unidades:
x
x2 + 12 = 22
x2 = 4 - 1
3
2
x 
3
x 

3
Sen 30º =
Cos 30º =
Tg 30º =
Cotg 30º=
Cosec 30º =
2
1
2
3
2
1
2

3
3
3
3
3
1
3
1




3
1
3

Sec 30º =
3
3
2
3
3
3
2
3
2





19. Sen 60º =
Cos 60º =
Tg 60º =
Cotg 60º =
Cosec 60º =
Sec 60º =
Sen 30º =
Cos 30º =
Tg 30º =
Cotg 30º=
Cosec 30º =
2
1
Sec 30º =
2
3
3
3
3
3
3
2
2
2
1
2
3
3
3
3
3
3
2
2

20. Cuadro resumen valor de funciones trigonometricas
de 30º 45º y 60º:
Ejercicios:
1) Calcular el valor de las siguientes expresiones:
Sen Cos Tg Cotg Sec Cosec
30º
45º
60º
2
1
2
1
2
3
2
3
3
3
3
3
3
3
3
3
2
3
3
2
2
2
2
2
2
2
2
2
1 1

21. (a) Cotg 60o-(Cos 30o - Cosec 60o) =









3
3
2
2
3
3
3
6
3
4
3
3
3
2
3
3
2
2
3
3
3 





2 3 2
6
3
3

2
3


22. (b) (Sen 45º-Tg 30º)(Cotg 60º+Sec 30º) =















3
3
2
3
3
3
3
2
2
3
3
3
3
3
2
2









1
3
3
3
2
2









3
9
2
6


3
3
2
6


1
2
6


2
2
6 


23. 2) Calcular la medida de los lados pedidos en cada uno
de los siguientes triángulos rectángulos:
Sen 60º =
x
6
x
6
2
3

Tg 60º =
y
6
y
6
3 
 
6
2
x
3 


3
3
12
3
3
3
12
3
12
x 




3
4
x 
6
y
3 

3
3
6
3
3
3
6
3
6
y 




3
2
y 

24. x
2
2
2
3

2
2
y
3
3

 
2
2
2
x
3 


3
6
4
3
3
3
2
4
3
2
4
x 




3
6
4
x 
2
2
3
y
3 


3
6
2
y 
Cos 30º =
x
2
2
Tg 30º =
2
2
y

25. 6
x
2
2


6
2
x
2 


2
3
2
2
3
4
2
12
x 



3
x 
Sen 45º =
6
x
Cos 45º =
6
y
6
y
2
2


6
2
x
2 


2
3
2
2
3
4
2
12
y 



3
y 

26. 3) Calcular el ángulo indicado en c/u de los siguientes
triángulos rectángulos:
8
3
4
x
Cos 
2
3
x
Cos 
 x = 30º
2
3
2
x
Tg 
3
x
Tg 
 x = 60º

27. 6
2
3
x
Sen 
2
2
x
Sen 
 x = 45º

28. Angulos de elevación y depresión:
Si OB linea visual sobre
OA linea horizontal;
luego  es ángulo de
elevación.
Si OB linea visual bajo
OA linea horizontal;
luego  es ángulo de
depresión.
Problemas:

29. a) Calcular la altura de una torre si al alejarnos 100
metros de su base, se obtiene un punto el que determina
una visual a la parte más alta de la torre la que forma
con la superficie un ángulo de elevación de 60o.
x
60º
100
x
3 

x
3
100 
.
m
3
100
x 
Tg 60º =
100
x
Se busca una función trigonométrica que
relacione los datos dados, en este caso el la
100m.
tangente.

30. b) Desde lo alto de un faro de 72 metros de altura se
observa una embarcación en el mar, determinandose una
línea visual con un ángulo de depresión de 30o.¿A que
distancia se encuentra la embarcación de la base del
faro?
72m
30º
30º
x m.
Se busca una función trigonométrica que
relacione los datos dados, en este caso el la
tangente.
x
72
3
3


Tg 30º =
x
72
72
3
x
3 


3
3
3
216
3
216
x




.
m
3
72
x 
3
3
216
x 

31. c) Un niño eleva un volantín dandole 300 metros de hilo.
Si el hilo forma con la superficie un ángulo de elevación
de 60o.¿A que altura se encuentra el volantín?
60º
x m
300
x
2
3


Sen 60º =
300
x
3
300
x
2 


2
3
300
x


.
m
3
150
x 
Se busca una función trigonométrica que
relacione los datos dados, en este caso es el
seno.

32. d) Un esquiador desciende una colina de 108 metros de
altura con un ángulo de depresión de 30o.¿Qué
distancia recorre el esquiador desde la cúspide hasta
llagar al plano?
108 m
30º
30º x
108
2
1


Sen 30º =
x
108
108
2
x
1 


.
m
216
x 
Se busca una función trigonométrica que
relacione los datos dados, en este caso es el
seno.