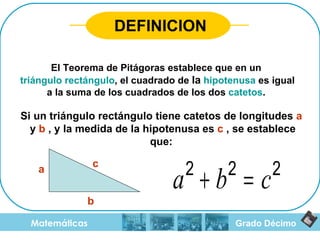
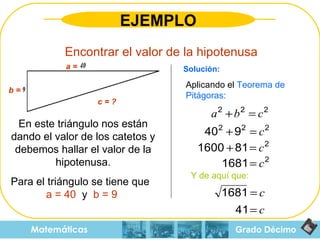
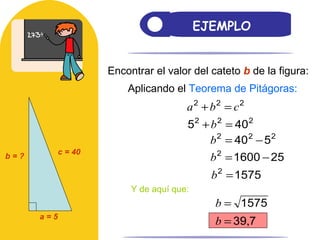
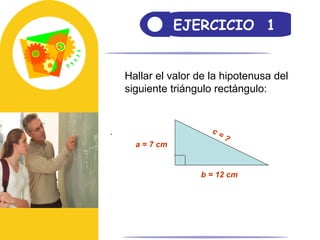
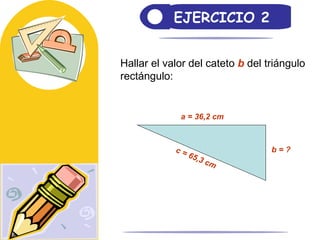
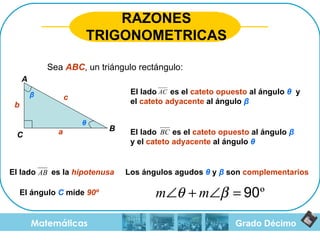
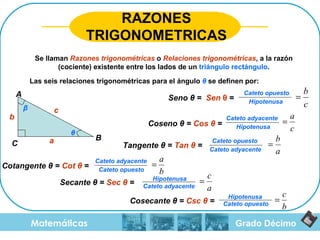
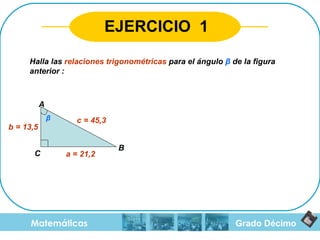
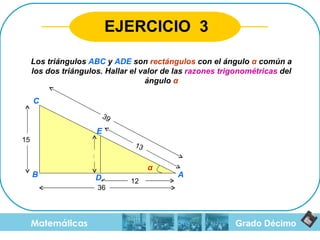
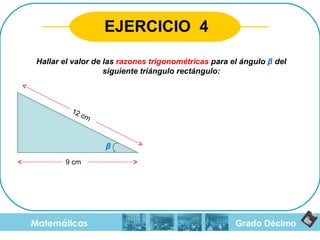
El documento aborda el teorema de Pitágoras, el cual establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. También se mencionan las razones trigonométricas y sus definiciones dentro del contexto de triángulos rectángulos, con ejemplos y ejercicios para el cálculo de hipotenusa y catetos. Además, se proporciona una breve historia del teorema, incluyendo su uso en civilizaciones antiguas como Mesopotamia y Egipto.

1. Activando proyección…………………………. COLEGIO JOSE ANTONIO GALAN MATEMATICAS, GRADO DECIMO PROFESOR: FREDY RODRIGUEZ

2. TEOREMA DE PITAGORAS

3. Grado Décimo Matemáticas El Teorema de Pitágoras establece que en un triángulo rectángulo , el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los dos catetos . DEFINICION Si un triángulo rectángulo tiene catetos de longitudes a y b , y la medida de la hipotenusa es c , se establece que: a b c

4. Grado Décimo Matemáticas HISTORIA El Teorema de Pitágoras lleva este nombre porque su descubrimiento recae sobre la escuela pitagórica . Anteriormente, en Mesopotamia y el Antiguo Egipto se conocían ternas de valores que se correspondían con los lados de un triángulo rectángulo, y se utilizaban para resolver problemas referentes a los citados triángulos, tal como se indica en algunas tablillas y papiros , pero no ha perdurado ningún documento que exponga teóricamente su relación.

5. Grado Décimo Matemáticas HISTORIA El Teorema de Pitágoras es de los que cuentan con un mayor número de demostraciones diferentes, utilizando métodos muy diversos. Una de las causas de esto es que en la Edad Media se exigía una nueva demostración de él para alcanzar el grado de Magíster matheseos .

6. Grado Décimo Matemáticas EJEMPLO Encontrar el valor de la hipotenusa En este triángulo nos están dando el valor de los catetos y debemos hallar el valor de la hipotenusa. Para el triángulo se tiene que a = 40 y b = 9 Aplicando el Teorema de Pitágoras: Y de aquí que: Solución: c = ? a = b =

7. EJEMPLO Encontrar el valor del cateto b de la figura: Aplicando el Teorema de Pitágoras: Y de aquí que: c = 40 a = 5 b = ?

8. EJERCICIO 1 . Hallar el valor de la hipotenusa del siguiente triángulo rectángulo: a = 7 cm b = 12 cm c = ?

9. EJERCICIO 2 Hallar el valor del cateto b del triángulo rectángulo: a = 36,2 cm c = 65,3 cm b = ?

10. EJERCICIO 3 Halla la altura de un triángulo isósceles cuyos Lados miden c = 5 cm . y a = b = 4 cm. c = 5 cm. b = 4 cm. a = 4 cm. h

11. EJERCICIO 4 El tamaño de las pantallas de televisión viene dado por la longitud en pulgadas de la diagonal de la pantalla ( una pulgada equivale a 2,54 cm ). Si un televisor mide 34,5 cm de base y 30 cm de altura, ¿cuál será su tamaño? 30 cm. 34,5 cm. d

12. Grado Décimo Matemáticas RAZONES TRIGONOMETRICAS Sea ABC , un triángulo rectángulo: El ángulo C mide 90º Los ángulos agudos θ y β son complementarios a b c θ β A B C El lado es el cateto opuesto al ángulo θ y el cateto adyacente al ángulo β El lado es el cateto opuesto al ángulo β y el cateto adyacente al ángulo θ El lado es la hipotenusa

13. Grado Décimo Matemáticas RAZONES TRIGONOMETRICAS Se llaman Razones trigonométricas o Relaciones trigonométricas , a la razón (cociente) existente entre los lados de un triángulo rectángulo . Las seis relaciones trigonométricas para el ángulo θ se definen por: a b c θ β A B C Coseno θ = Cos θ = Cateto adyacente Hipotenusa Tangente θ = Tan θ = Cateto opuesto Cateto adyacente Cotangente θ = Cot θ = Cateto adyacente Cateto opuesto Secante θ = Sec θ = Cateto adyacente Hipotenusa Seno θ = Sen θ = Cateto opuesto Hipotenusa Cosecante θ = Csc θ = Cateto opuesto Hipotenusa

14. Grado Décimo Matemáticas EJERCICIO 1 Halla las relaciones trigonométricas para el ángulo β de la figura anterior : a = 21,2 b = 13,5 c = 45,3 β A B C

15. Grado Décimo Matemáticas EJERCICIO 2 Construya cada uno un triángulo rectángulo donde el ángulo θ = 60º y halle cada una de las relaciones trigonométricas del ángulo θ

16. Grado Décimo Matemáticas EJERCICIO 3 Los triángulos ABC y ADE son rectángulos con el ángulo α común a los dos triángulos. Hallar el valor de las razones trigonométricas del ángulo α 15 12 36 13 39 5 α A B C D E

17. Grado Décimo Matemáticas EJERCICIO 4 Hallar el valor de las razones trigonométricas para el ángulo β del siguiente triángulo rectángulo: 9 cm 12 cm β

18. Grado Décimo Matemáticas EJERCICIO 5 Si se sabe que , calcular las demás funciones trigonométricas para el ángulo θ