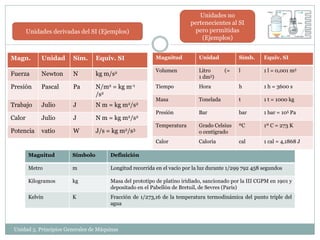
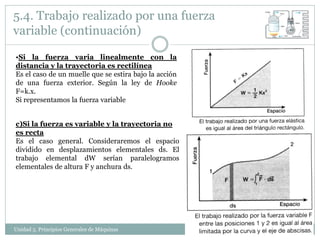
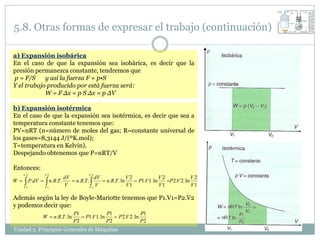
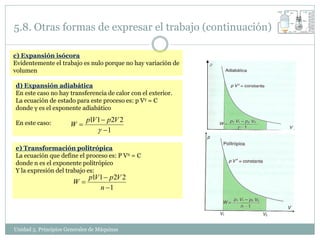
Este documento describe los principios básicos de las máquinas. Explica que una máquina transforma la energía para desarrollar un efecto físico y clasifica las máquinas en eléctricas, térmicas y otras. También define conceptos como trabajo, energía, potencia y diferentes formas de energía como cinética, potencial y térmica. Resalta que la energía se conserva pero puede transformarse de una forma a otra.

1. Tecnología Industrial II
Bachillerato de Ciencias y Tecnología
Principios generales de máquinas
IES PEDRO SIMÓN ABRIL
(ALCARAZ)

2. 5.1.-5.2. Concepto de máquina.
Magnitudes y Unidades
Máquina es: todo medio creado por el hombre que se encarga de recibir y transformar
la energía de forma adecuada para desarrollar un determinado efecto físico. Un
máquina transforma los dos factores del trabajo: la fuerza y el espacio.
En el estudio de las máquinas distinguiremos:
a) Máquinas eléctricas: generadores (transforman la energía mecánica en eléctrica),
motores (transforman la energía eléctrica en mecánica) y transformadores (transforman la
energía magnética en eléctrica)
b) Máquinas térmicas: motrices y frigoríficas. Magnitud Unidad SI Símbolo
Las magnitudes referidas a máquinas: masa, energía, Longitud Metro m
potencia…, se expresarán en el SI.
Recordemos que las unidades básicas del SI son: Masa Kilogramos kg
Cantidad de Mol mol
materia
Tiempo Segundos s
Intensidad Amperios A
Unidad Equiv.:1 kp (1 kgf) = 9,8 N eléctrica
Temperatura Kelvin K
Unidad 5. Principios Generales de Máquinas

3. Unidades no
pertenecientes al SI
Unidades derivadas del SI (Ejemplos) pero permitidas
(Ejemplos)
Magn. Unidad Sím. Equiv. SI Magnitud Unidad Símb. Equiv. SI
Volumen Litro (= l 1 l = 0,001 m3
Fuerza Newton N kg m/s2 1 dm3)
Presión Pascal Pa N/m2 = kg m-1 Tiempo Hora h 1 h = 3600 s
/s2
Masa Tonelada t 1 t = 1000 kg
Trabajo Julio J N m = kg m2/s2
Presión Bar bar 1 bar = 105 Pa
Calor Julio J N m = kg m2/s2
Temperatura Grado Celsius ºC 1º C = 273 K
Potencia vatio W J/s = kg m2/s3 o centígrado
Calor Caloria cal 1 cal = 4,1868 J
Magnitud Símbolo Definición
Metro m Longitud recorrida en el vacío por la luz durante 1/299 792 458 segundos
Kilogramos kg Masa del prototipo de platino iridiado, sancionado por la III CGPM en 1901 y
depositado en el Pabellón de Bretuil, de Sevres (Paris)
Kelvin K Fracción de 1/273,16 de la temperatura termodinámica del punto triple del
agua
Unidad 5. Principios Generales de Máquinas

4. 5.3. Trabajo
Se denomina trabajo realizado sobre un cuerpo al producto escalar de la fuerza aplicada sobre
el cuerpo por el desplazamiento producido sobre el cuerpo. Se mide en julios, en calorías
(4,18 julios) y en kwh (3.600.000 julios).
W  F .s  F .s. cos
Si la fuerza coincide en dirección y sentido con el desplazamiento φ=0 y entonces cosφ=1 con lo que
W=F.s
- Si cosφ es positivo diremos que se realiza trabajo motor o útil
- Si cosφ es negativo diremos que se realiza trabajo resistente
En el Sistema Técnico, la unidad de fuerza es el kilopondio o kilogramo-fuerza y la unidad de
longitud el metro, con lo que la unidad de trabajo se conoce como kilopondímetro (prácticamente en
desuso)
1 kilopondímetro (kpm) = 1 kilopondio (kp) • metro (m)
Equivalencia: 1 kpm = 9,8 J
Unidad 5. Principios Generales de Máquinas

5. 5.4. Trabajo realizado por una fuerza
variable
La definición anterior supone que la fuerza que realiza el trabajo es constante y que además la trayectoria
seguida por el móvil es rectilínea pero esto no siempre sucede (por ejemplo en un motor de explosión).
Cuando esto no sucede consideraremos lo siguiente:
ds incremento de desplazamiento elemental.
dW incremento infinitesimal de trabajo.
Se obtiene que dW  F .d s  F . cos.s B
Y el trabajo total correspondiente al desplazamiento entre una posición elemental A y otra final B será: W   F .d s
A
Así se pueden plantear las siguientes situaciones:
•Si la fuerza es constante y la trayectoria es
rectilínea
Representando en unos ejes coordenados la fuerza
en ordenadas y el desplazamiento en abscisas, el
valor numérico del trabajo es el valor del área del
rectángulo; es decir el producto W=F.s.
Unidad 5. Principios Generales de Máquinas

6. 5.4. Trabajo realizado por una fuerza
variable (continuación)
•Si la fuerza varia linealmente con la
distancia y la trayectoria es rectilínea
Es el caso de un muelle que se estira bajo la acción
de una fuerza exterior. Según la ley de Hooke
F=k.x.
Si representamos la fuerza variable
c)Si la fuerza es variable y la trayectoria no
es recta
Es el caso general. Consideraremos el espacio
dividido en desplazamientos elementales ds. El
trabajo elemental dW serían paralelogramos
elementales de altura F y anchura ds.
Unidad 5. Principios Generales de Máquinas

7. 5.4. Trabajo realizado por una fuerza
variable (continuación)
Si no se desean hacer cálculos con integrales se
podría calcular el área de modo aproximativo a base
de rectángulos elementales, aumentando la F
precisión a medida que aumenta el número de
rectángulos elementales:
X
W=SFi.Dx
Dx
Donde:
∑ = represente el sumatorio de todos los productos F● Δx en los diferentes
intervalos que consideremos. F adquirirá diferente valor en cada intervalo.
Unidad 5. Principios Generales de Máquinas

8. 5.5. Formas de energía.
Conservación de la energía
La energía se puede definir como la capacidad para producir un trabajo.
Se mide en Julios, calorías o kwh
Entre las diferentes formas de energía podemos destacar:
A) Energía mecánica (cinética + potencial)
Es la energía almacenada en los cuerpos materiales y que puede definirse como la capacidad que
tiene un cuerpo para realizar trabajo en función de su velocidad (cinética), de su
posición en un campo gravitatorio (potencial gravitatoria), de su estado de tensión
(potencial elástico), etc.
A.1. Energía cinética
Es la energía que posee un cuerpo en virtud de su movimiento.
E cinética=Energía cinética de traslación + Energía cinética de rotación
a.1)Energía cinética de traslación. Es la energía cinética que posee el cuerpo debido a su
movimiento de traslación.
Ec = ½ m v2 Ec = energía cinética en Julios (J)
m = masa (kg)
v = velocidad lineal (m/s)
Unidad 5. Principios Generales de Máquinas

9. 5.5. Formas de energía.
Conservación de la energía (continuación)
a.2) Energía cinética de rotación. Es la energía cinética que posee un cuerpo debido a su
movimiento de giro alrededor de un eje. Si v=ώ r entonces Ec = ½ mr2ώ2. La Ec total será la suma de
la s energías cinéticas individuales de todas las partículas: Ec = ½ (m1r12 + m2r22 +…) ώ2
Así: Ec = ½ I ώ2 Ec = energía cinética de rotación (J)
I = momento de inercia (kg m2)
ώ = velocidad angular (rad/s)
El Momento de Inercia (I) es un parámetro que depende de la masa y de
la geometría del material. Se obtiene al sumar la energía cinética de todas las
partículas que giran con el cuerpo (∑miri2)
b)Energía potencial gravitatoria
Es la energía que posee un cuerpo en función de su altura respecto de la
superficie de la tierra
Ep  m.g.h. Ep= energía potencial (J)
m = masa (kg)
g = aceleración de la gravedad (m/s2)
h = altura (m)
Unidad 5. Principios Generales de Máquinas

10. 5.5. Formas de energía.
Conservación de la energía (continuación)
A.2. Energía térmica:
Es una forma de energía en tránsito consecuencia de la diferencia de Tª entre dos
cuerpos en contacto. Es el calor absorbido por un cuerpo. Es proporcional a la cantidad
de masa, calor específico e incremento de temperatura del mismo:
Q = m C Δt
La unidad de expresión de Q en el SI es el Julio. También se puede emplear la caloría (cal). Cuando un
cuerpo absorbe energía en forma de calor:
a) El cuerpo se dilata, aumenta su volumen, lo que genera trabajo.
b) Aumenta la movilidad atómica, y en consecuencia la energía interna del material, lo que
se manifiesta en un aumento de temperatura.
En los gases diferenciaremos:
a) Energía térmica con calor específico a volumen constante: Qv = m Cv Δt
b) Energía térmica con calor específico a presión constante: Qp = m Cp Δt
En los gases es preferible expresar el calor específico utilizando en número de moles en lugar de la
masa, ya que de esta manera la diferencia entre Cp y Cv es aproximadamente la constante R de la
ecuación de los gases perfectos si se expresa el calor en calorías.
Ecuación de Mayer: Cp – Cv = R = 2 cal/K•mol
Unidad 5. Principios Generales de Máquinas

11. Principio de conservación de la energía
La energía no se crea ni se destruye, solamente se transforma.
El principio de conservación también es aplicable a la masa, de acuerdo con la ecuación de
Einstein: E = m•c2 E = energía (Julios)
m = masa (kg)
c = velocidad de la luz (m/s)
El principio de conservación de la energía aplicado a máquinas térmicas se denomina Primer
Principio de la Termodinámica. El objetivo es aprovechar el calor para producir trabajo
(motor térmico) o emplear el trabajo para extraer calor (máquina frigorífica). Así pues por
aplicación de Primer Principio de la Termodinámica obtenemos que :
ΔU = Q – W ΔU = variación de energía interna
Q = calor
W = trabajo
Q -W
a) en motores térmicos: Q = ΔU + W
b) en máquinas frigoríficas: W = ΔU + Q SISTEMA
En este principio no se ha tenido en cuenta el rozamiento. -Q W
Como sabemos no toda la energía es aprovechable, lo que nos conduce
al concepto de rendimiento (η).
Unidad 5. Principios Generales de Máquinas

12. 5.6. Potencia
Se define la potencia como la variación del trabajo por unidad de tiempo.
P = W/t su unidad en el SI es el vatio=julio/segundo
La potencia también se puede calcular mediante la expresión: W F .s
P   F .v
t t
Donde v = velocidad del cuerpo al que se le aplica la fuerza.
La potencia también se puede expresar en kilovatios (kW), caballos de vapor (CV=735 W) e incluso
caballos-fuerza (HP=746W (sistema anglosajón)).
Una particularidad del trabajo como magnitud física, en comparación con otras, es que tiene valor
monetario. Se fija el precio del kWh, lo que no sucede con el N o m/s.
5.7. Resistencias pasivas. Rendimiento mecánico
Al producirse un trabajo se generan unas pérdidas o energía no utilizable que se puede denominar
trabajo de rozamiento y que normalmente se disipa en forma de calor.
W  DEp  DEc  Wr
Unidad 5. Principios Generales de Máquinas

13. 5.7. Resistencias pasivas. Rendimiento mecánico
(continuación)
Como ya sabemos la fuerza de rozamiento es el producto de la acción normal entre el cuerpo y la superficie
que lo soporta, N, y un coeficiente de rozamiento, μ, que depende de la naturaleza de la superficie: Fr = N μ
Además existen otros trabajos no útiles, trabajos pasivos debidos a esfuerzos y resistencias pasivas, como
resistencia de fluidos, tensiones de cables, etc.
Las máquinas son dispositivos que transforman una energía o un trabajo de una clase determinada en otra
energía u otro trabajo.
Llamaremos:
-Wm=trabajo motor o energía de entrada
-Wu= trabajo útil o energía de salida
-Wr=trabajo resistente o perdidas
Como es evidente: Wm = Wu + Wr
Así el rendimiento de una máquina se define como el cociente entre el trabajo útil y el trabajo
motor
Wu Wm  Wr Wr
   1
Wm Wm Wm
En función de la potencia sería:
Pu Pm  Pr Pr
   1
Pm Pm Pm
En el caso de máquinas puestas consecutivamente en cadena de manera que cada una de ellas use la energía
transformada por la anterior el rendimiento de toda la instalación será el producto de todos los rendimientos
de cada una de las máquinas
  1 . 2 .... n
Unidad 5. Principios Generales de Máquinas

14. 5.7. Resistencias pasivas. Rendimiento mecánico
(continuación)
Hemos de tener en cuenta que las máquinas no funcionan siempre a la velocidad de régimen. En una
máquina existen diferentes periodos de marcha; algunos de los más importantes son:
a) Arranque: el trabajo motor (Wm) se emplea en pasar de la velocidad 0 al valor de régimen v,
además en vencer las resistencias pasivas y realizar trabajo útil.
Wm  Wu  Wr   Ec
Ec= energías cinéticas de rotación y traslación de los diferentes órganos
b) Régimen normal: el trabajo motor ya ha vencido la inercia, ha adquirido la velocidad v que
se mantiene constante, por lo que ya no varía la Ec, así:
Wm  Wu  Wr
c) Parada: la Ec se devolverá, pues se pasa de velociad v a velocidad 0, o bien se disipa en alguno
de los sistemas de freno.
Wm  Wu  Wr   Ec
Unidad 5. Principios Generales de Máquinas

15. 5.8. Otras formas de expresar el trabajo
En la rotación de un cuerpo, se produce el giro alrededor de un punto por acción de una fuerza
•Momento de una fuerza respecto de un punto:
Es el producto de la fuerza por la distancia mínima al punto M=F.d. El momento se mide en N.m.
•Trabajo de rotación
Se define el trabajo de rotación como: W   M .d
donde σ es el ángulo girado en radianes.
En el caso de que M no varíe se obtiene que W=M.σ siendo σ el ángulo girado en radianes.
•Trabajo de expansión-compresión en un cilindro
El gas que queda encerrado en un cilindro puede evolucionar en su interior de diversas formas:
- A presión constante o isobárica
- A temperatura constante o isoterma
- A volumen constante o isócora
- Sin intercambio de calor o adibática
- Como generalización de las anteriores, politrópica
Por la importancia de estas transformaciones en las máquinas térmicas, vamos a estudiar cada una de
ellas.
Unidad 5. Principios Generales de Máquinas

16. 5.8. Otras formas de expresar el trabajo (continuación)
a) Expansión isobárica
En el caso de que la expansión sea isobárica, es decir que la
presión permanezca constante, tendremos que
p = F/S y así la fuerza F = p•S
Y el trabajo producido por está fuerza será:
W = F Δx = p S Δx = p ΔV
b) Expansión isotérmica
En el caso de que la expansión sea isotérmica, es decir que sea a
temperatura constante tenemos que:
PV=nRT (n=número de moles del gas; R=constante universal de
los gases=8,3144 J/(ºK.mol);
T=temperatura en Kelvin).
Despejando obtenemos que P=nRT/V
Entonces:
V2 V2 V2
dV dV V2 V2 V2
W  P.dV   n.R.T .
V1 V1
V
 n.R.T . 
V1
V
 n.R.T . ln
V1
 P1.V 1. ln
V1
P2.V 2. ln
V1
Además según la ley de Boyle-Mariotte tenemos que P1.V1=P2.V2
y podemos decir que:
P1 P1 P1
W  n.R.T . ln  P1.V 1. ln  P2.V 2. ln
P2 P2 P2
Unidad 5. Principios Generales de Máquinas

17. 5.8. Otras formas de expresar el trabajo (continuación)
c) Expansión isócora
Evidentemente el trabajo es nulo porque no hay variación de
volumen
d) Expansión adiabática
En este caso no hay transferencia de calor con el exterior.
La ecuación de estado para este proceso es: p Vγ = C
donde γ es el exponente adiabático
p1V 1  p2V 2
En este caso: W
 1
e) Transformación politrópica
La ecuación que define el proceso es: P Vn = C
donde n es el exponente politrópico
Y la expresión del trabajo es:
p1V 1  p 2V 2
W
n 1
Unidad 5. Principios Generales de Máquinas

18. 5.8. Otras formas de expresar el trabajo (continuación)
•Energía y potencia eléctrica
a) Intensidad de corriente eléctrica: cantidad de carga eléctrica que circula en la unidad de
tiempo:
I = Δq/t I = Intensidad en Amperios (A)
q = Carga eléctrica en Culombios (C)
t = tiempo en segundos (s)
b) Diferencia de potencial: trabajo necesario para mover la unidad de carga eléctrica entre dos
puntos de un campo eléctrico:
ΔU = W/q ΔU = Diferencia de potencial en Voltios (V)
W = Trabajo en Julios (J)
q = Carga eléctrica en Culombios (C)
Si el W = 0 esto implica que la carga se mueve entre dos puntos que están al mismo potencial. Las
superficies de un campo eléctrico que se encuentran al mismo potencial se denominan
Equipotenciales.
Así si el W = q U y q = I t podemos establecer que : W = U I t
Como la potencia es el trabajo realizado en la unidad de tiempo: P = U I t/t = U I
La energía consumida por un dispositivo eléctrico sería: E = P t
E = energía en kWh
P = potencia en kilovatios (kW)
t = tiempo en horas (h)
Unidad 5. Principios Generales de Máquinas

19. 5.8. Otras formas de expresar el trabajo (continuación)
• Potencia hidráulica
Sabemos que la potencia (P) es: w F d
P   F v
t t
Cuando trabajamos con fluidos la fuerza es la presión ejercida sobre la superficie: F  PS
En cuanto a la velocidad, por aplicación del principio de continuidad, será:
Q
v
Por tanto, operando obtenemos: S
Q
P  pS  p Q
S
siendo: P = potencia en vatios (W)
p = presión en Pascales (Pa = N/m2)
Q = caudal en m3/s
Otra forma de calcular la potencia hidráulica es: P  Q.h
siendo: P = potencia en vatios (W)
Q = caudal en m3/s
h = altura o desnivel en m
Unidad 5. Principios Generales de Máquinas