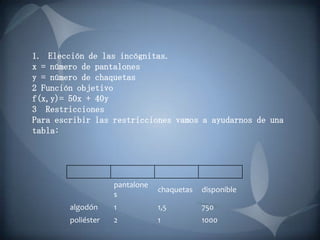
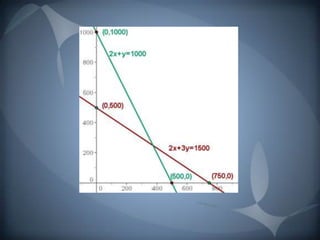
La programación lineal es un procedimiento matemático para resolver problemas formulados como ecuaciones lineales para obtener un resultado óptimo. Se usa un modelo matemático con funciones lineales para describir el problema y encontrar la mejor solución. En un ejemplo, un fabricante debe maximizar sus ventas suministrando la cantidad óptima de pantalones y chaquetas a un almacén usando la cantidad disponible de tejidos, considerando restricciones como la materia prima requerida para cada producto.

1. ESCUELA POLITECNICA DEL EJERCITO
COMPUTACION AVANZADA
PROGRAMACIÓN LINEAL
GISSELA PAREDES
THALIA CUEVA
DAYSI SINALUIZA

2. DEFINICION
Es un procedimiento o algoritmo matemático mediante el
cual se resuelve un problema indeterminado, formulado a
través de ecuaciones lineales.
Es una técnica determinista, no incluye probabilidades y
utiliza un modelo matemático para describir el problema.
El adjetivo lineal significa que todas las funciones
matemáticas del modelo deben ser funciones lineales. En
este caso, la palabra programación no se refiere a
programación en computadoras; en esencia es un sinónimo
de planeación. Así, la PL trata la planeación de las
actividades para obtener un resultado óptimo, esto es, el
resultado que mejor alcance la meta especificada (según el
modelo) entre todas las opciones de solución.

5. EJEMPLO:
Unos grandes almacenes encargan a un fabricante pantalones y
chaquetas deportivas.
El fabricante dispone para la confección de 750 m de tejido de
algodón y 1000 m de tejido de poliéster. Cada pantalón precisa 1 m
de algodón y 2 m de poliéster. Para cada chaqueta se necesitan 1.5
m de algodón y 1 m de poliéster.
El precio del pantalón se fija en 50 € y el de la chaqueta en 40 €.
¿Qué número de pantalones y chaquetas debe suministrar el
fabricante a los almacenes para que éstos consigan una venta
máxima?

6. 1. Elección de las incógnitas.
x = número de pantalones
y = número de chaquetas
2 Función objetivo
f(x,y)= 50x + 40y
3 Restricciones
Para escribir las restricciones vamos a ayudarnos de una
tabla:
pantalone
chaquetas disponible
s
algodón 1 1,5 750
poliéster 2 1 1000

7. x + 1.5y ≤ 750 2x+3y≤1500
2x + y ≤ 1000
Como el número de pantalones y chaquetas son números
naturales, tendremos dos restricciones más:
x≥0
y≥0
4 Hallar el conjunto de soluciones factibles
Tenemos que representar gráficamente las restricciones.
Al ser x ≥ 0 e y ≥ 0, trabajaremos en el primer cuadrante.
Representamos las rectas, a partir de sus puntos de corte
con los ejes.