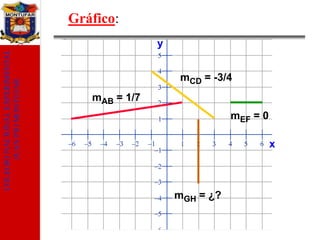
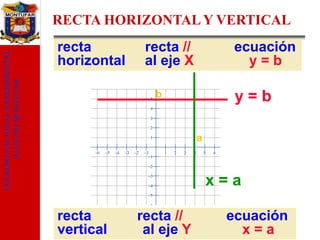
El documento presenta información sobre la pendiente de una recta. Explica conceptos como la pendiente, el cálculo de la pendiente entre dos puntos y diferentes formas de representar una recta mediante ecuaciones. Además, introduce conceptos relacionados como rectas paralelas y perpendiculares. El objetivo es explicar y analizar la noción de pendiente de una recta en geometría.

2. COLEGIO NACIONAL EXPERIMENTAL
“JUAN PIO MONTUFAR”
PROYECTO DE GEOMETRIA
PENDIENTE DE
UNA RECTA

3. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR
OBJETIVOS:
1. Explicar el concepto de pendiente.
2. Determinar la pendiente de una recta.
3. Identificar los elementos que determinan una
recta.
4. Dada una recta l en un plano de coordenadas,
deducir una ecuación cuya gráfica corresponda
a l.

4. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR
Internet
Wikipedia
Power Point
Microsoft Word
Geometría Analítica
de Lehmann
Página de Internet:
www.wikipedia.org
AutoCad (2010)
Visual Basic
Html

5. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR
PROCEDIMINETO
 Se nos otorgo el tema de “Pendiente de una Recta” para su
desarrollo.
 Consultamos en las diferentes fuentes de información todo lo
que encontramos acerca del tema.
 Lo organizamos de una manera didáctica mediante la
utilización de organizadores gráficos y ejemplos sencillos.
 Consultamos temas relacionados con nuestro tema principal
para complementar el conocimiento.
 Por último mediante el uso de graficadores comprobamos la
teoría consultada anteriormente.

6. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR
INDICE
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Ángulo de inclinación de una recta.
Pendiente de una recta.
Calculo de la pendiente de una recta.
Teorema de la pendiente de una recta.
Ejemplos de aplicación.
Conclusiones.
Ecuación de la recta 1.
Ecuación de la recta 2.
Ecuación de la recta 3.
Recta vertical y horizontal.
1. Rectas Paralelas.
2. Rectas perpendiculares.
11. Utilización de Graph para grafica pendientes.
12. Utilización de Autocad para graficar pendientes.

7. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR
ÁNGULO DE INCLINACION DE UNA RECTA
El ángulo de inclinación de la recta está formado por la parte
positiva del eje X y la recta considerada hacia arriba.
y
Se halla en el intervalo de:
0º≤ ω ≤180º
ω
ω
x

8. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR
Pendiente de una Recta
Se llama pendiente de una
recta, a la tangente de su
ángulo de inclinación.
Se la representa con
la letra “m”.
m = tg ω
Si ω es agudo la
pendiente es positiva
Si ω es obtuso la
pendiente es
negativa
Cualquier recta que coincida o que sea paralela al
ángulo de inclinación de 90º no existe ya que tg de 90º
no esta definida

9. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR
Ejemplo:
Calcule la pendiente (m) del siguiente
gráfico:
ω= 45º
m = tg ω
ω
m = tg 45º
m=1

10. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR
Cálculo de la pendiente de una recta
Sea l una recta no vertical que pasa
por los puntos P1(x1;y1) y P2(x2; y2).
y
P2(x2; y2)
y=y2 - y1
P1(x1;y1)
0
x=x2 - x1
x
y2 - y1
m= x -x
2
1

11. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR
Teorema de la Pendiente de una Recta
Teorema
• Si P1 y P2 son 2 puntos diferentes cualesquiera
de una recta, la pendiente de la recta es igual a:
Teniendo en cuenta que:

12. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR
Ejemplos
Ubique los puntos en el plano y
determine la pendiente de estos
segmentos:
1. A(-6; 1)
y B(1; 2)
2. C(-1; 4) y
D(3; 1)
3. E(3; 2)
y
F(8; 2)
4. G(2; 1)
y
H(2; -3)

13. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR
Desarrollo:

14. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR
Gráfico:
y
mCD = -3/4
mAB = 1/7
mEF = 0
x
mGH = ¿?

15. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR
Conclusiones
1. Si m>0 la recta l es creciente
2. Si m<0 la recta l es decreciente
3. Toda recta horizontal tiene m = 0
4. Las rectas verticales no tienen
pendiente definida.

16. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR
Ecuación de la recta 1.
La ecuación de la recta de pendiente m, y
punto de paso (x1, y1) es:
Y
(x1, y1)
y - y1 = m(x - x1)
X

17. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR
Ecuación de la recta 2.
La gráfica de una recta de pendiente m y
ordenada en el origen b, es:
Y
y = mx + b
b
X

18. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR
Ecuación de la recta 3.
ECUACIÓN GENERAL DE LA RECTA
Ax + By + C = 0
La gráfica de una ecuación lineal:
Ax + By + C = 0, es una recta, y recíprocamente,
toda recta es la gráfica de una ecuación lineal.

19. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR
RECTA HORIZONTAL Y VERTICAL
recta
horizontal
recta //
al eje X
ecuación
y=b
y=b
b
a
x=a
recta
vertical
recta //
al eje Y
ecuación
x=a

20. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR
En resumen:
Formas de la ecuación de una recta:
• Forma punto pendiente:
• Forma pendiente ordenada
al origen
• Forma general
y-y1=m(x-x1)
y = mx+b
Ax + By + C = 0
• Recta vertical
x=a
• Recta horizontal
y=b

21. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR
Rectas paralelas
Dos rectas l1 y l2 cuyas pendientes son m1 y m2 ,
son paralelas (l1 // l2) si y sólo si tienen la misma
pendiente o si ambas son verticales .
Es decir:
m1 = m 2

22. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR
Rectas perpendiculares
Dos rectas l1 y l2 cuyas pendientes son m1 y m2 ,
son perpendiculares (l1 l2) si y sólo si el producto
de sus pendientes es -1.
Es decir:
m1 . m2 = -1
Además, una recta horizontal y una vertical son
perpendiculares entre sí.

23. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR
Ejercicios:
1.- Determine la ecuación de la recta que pasa por (5/2; 5) y tiene pendiente 1/3.
2. Determine la ecuación de la recta que pasa por (6;1) y (1;4).
3. Determine la pendiente y la
intersección con el eje y de la recta determinada
por la ecuación x- 9 = 5y+3.
4. Determine la ecuación general de la
recta que pasa por (3; -1) y (-2;-9).

24. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR

25. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR

26. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR

27. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR

28. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR

29. COLEGIO NACIONAL EXPERIMENTAL
JUAN PIO MONTUFAR
