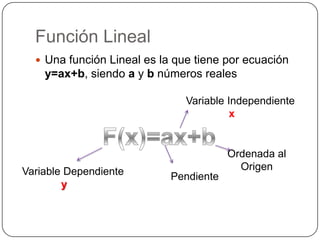
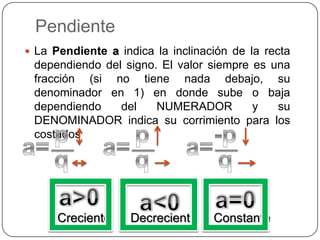
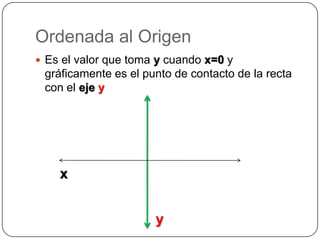
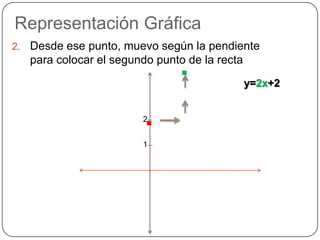
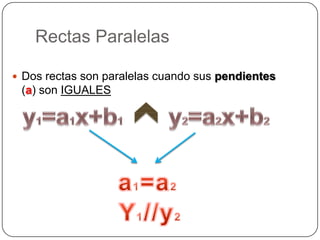
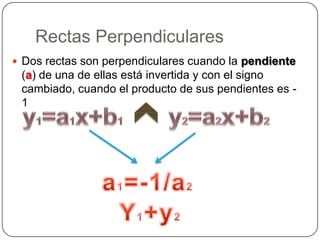
La función lineal se representa como y=ax+b, donde a es la pendiente y b es la ordenada al origen. La pendiente indica si la recta es creciente, decreciente o constante, mientras que la ordenada al origen es el punto donde la recta corta el eje y. Dos rectas son paralelas si tienen la misma pendiente y perpendiculares si el producto de sus pendientes es -1.

1. Graficos y EcuacionesFunción Lineal

2. Función LinealUna función Lineal es la que tiene por ecuación y=ax+b, siendo a y b números realesVariable Independiente xF(x)=ax+bOrdenada alOrigenVariable DependienteyPendiente

3. PendienteLa Pendiente a indica la inclinación de la recta dependiendo del signo. El valor siempre es una fracción (si no tiene nada debajo, su denominador en 1) en donde sube o baja dependiendo del NUMERADOR y su DENOMINADOR indica su corrimiento para los costadospp-pa=a=a=qqqa>0a=0a<0CrecienteDecrecienteConstante

4. Ordenada al OrigenEs el valor que toma y cuando x=0 y gráficamente es el punto de contacto de la recta con el eje yxy

5. Representación GráficaSe marca sobre el eje y la Ordenada al Origen (b), el punto por donde la recta va a cortar:y=2x+2.21

6. Representación Gráfica.Desde ese punto, muevo según la pendiente para colocar el segundo punto de la rectay=2x+2.21

7. Formas de la ecuación de una RectaCuando tenemos la pendiente y uno de los puntos de la recta:Ecuación de la recta que pasa por p=(x0;y0) y tiene Pendiente ay-y0=a(x-x0)

8. Formas de la ecuación de una RectaCuando tenemos dos puntos de la recta:Ecuación de la recta que pasa por p=(x0;y0) y q=(x1;y1)y1-y0(x-x0)y-y0=x1-x0

9. Rectas ParalelasDos rectas son paralelas cuando sus pendientes (a) son IGUALESy1=a1x+b1y2=a2x+b2a1=a2Y1//y2

10. Rectas PerpendicularesDos rectas son perpendiculares cuando la pendiente (a) de una de ellas está invertida y con el signo cambiado, cuando el producto de sus pendientes es -1y1=a1x+b1y2=a2x+b2a1=-1/a2Y1+y2