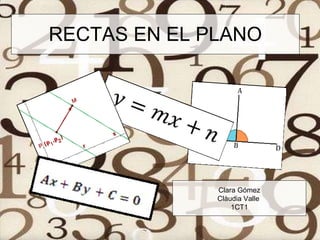
Este documento resume diferentes formas de representar rectas en un plano, incluyendo ecuaciones vectoriales, paramétricas, generales y explícitas. También explica cómo determinar la posición relativa entre rectas basada en sus pendientes, y cómo calcular la proyección ortogonal de un punto sobre una recta y el ángulo entre dos rectas.

1. RECTAS EN EL PLANO Clara Gómez Clàudia Valle 1CT1

3. Ecuación vectorial: (x,y) = (xº,yº)+k(a,b) Ecuaciones paramétricas: x = xº + k·a y = yº + k·b Ej: Ecuación contínua: x-xº y-yº a b 1 7 Vector director Punto genérico Punto conocido Vector director La información que se obtiene es la misma que la de la E. vectorial Vector director La información que se obtiene es la misma que la de la E. vectorial y la E. paramétricas Cada valor real de la k nos determina el punto x de la recta. Si conocemos la ecuación vectorial podemos conocer un punto y un vector. x= -1+3k y= 3+4k Ej: (x,y)= (-1,3)+k(3,4) Ej: x-3 y+2

4. E. general: Ax + By + C = 0 ( A, B 0 ) Asignando un valor a la x, tendremos inmediatamente la y, y por tanto las coordenadas de un punto de la recta. Ya que teniendo dos puntos podemos trazar una recta, basta con que hagamos este proceso dos veces para tener una recta definida. Además, esta ecuación permite saber la dirección, ya que A=b y B=-a, y por lo tanto tenemos el vector director. E. explícita: y = mx + n Pendiente Ordenada al origen A partir del pendiente se determina la posición relativa entre dos rectas: Perpendiculares: m r ·m s = -1 Paralelas: m r = m s Coincidentes: m r = m s ; n r =n s -> Son la misma recta Coeficientes de x Termino Independiente Ej: x-2y-5=0 Ej: y= 5x+8

5. Proyección ortogonal: Punto simétrico: M=punto exterior a la recta M ’ =e s la proyección ortogonal o la proyección de M sobre la recta. -Punto exterior -Proyección ortogonal -Punto simétrico Para encontrar el punto simétrico se utiliza la siguiente fórmula: P = ( x+a , y+b ) 2 2 La a y b son el punto simétrico, la x y la y son el punto exterior y la P es la proyección ortogonal. Angulo de dos rectas: Dos rectas que se cortan forman 4 ángulos, iguales dos a dos. cos β = | v∘w| |v|·|w| S i las dos rectas son paralelas: el ángulo será de 0º Si las rectas son perpendiculares: el ángulo será de 90º.