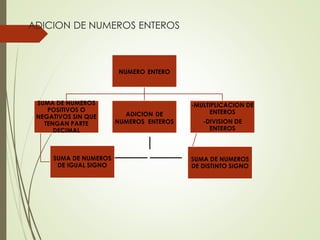
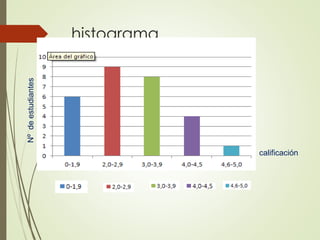
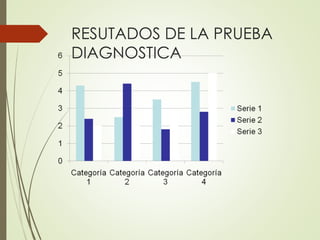
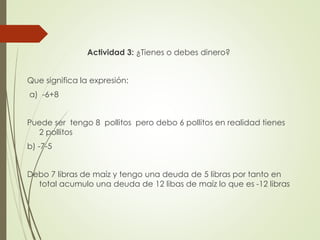
Este documento presenta tres estrategias didácticas para el aprendizaje de la adición de números enteros en estudiantes de séptimo grado. La primera estrategia implica interpretar situaciones cotidianas con números enteros. La segunda involucra planear y ejecutar los pasos para resolver problemas de adición de enteros. La tercera consiste en implementar actividades interactivas sobre el tema mediante las TIC. El objetivo general es que los estudiantes aprendan los conceptos básicos de números enteros y su adición aplicándolos a contextos reales.

1. ESTRATEGIAS
DIDACTICAS PARA EL
APRENDIZAJE DE LA
ADICIÓN DE NÚMEROS
ENTEROS

2. IDENTIFICACION
Nombre de la Institución:
Institución Educativa Técnica Agro pesquera Manuel Padilla Polo
de Robles el Guamo Bolívar
Nivel: Educación básica secundaria
Grado: séptimo
Sección: Diurna
Docente: Lic. Luis Felipe González Hernández

3. ÍNTRODUCCIÓN
Las áreas básicas del conocimiento no se pueden seguir
desarrollando en forma fragmentada y con poca
profundización. Metodológicamente se han venido
abordando en forma rígida y aislada, no potencian las
capacidades mas necesarias para satisfacer las exigencias
de la realidad social.
Este encasillamiento del saber escolar ha traído como
consecuencia el fracaso de los estudiantes de 7° de la IETA
Manuel Padilla Polo de Robles en la solución de sus
problemas extraescolares que suponen habilidades y
conocimientos de variada índole.

4. DIAGNOSTICO
AMBIENTE ESTUDIANTIL: En los estudiantes de 7° de la
Institución Educativa Técnica Agro pesquera
Manuel Padilla Polo de Robles el Guamo Bolívar
se identifica la situación :
Aspectos
cognoscitivos:
presentan
algunas
habilidades mentales para el proceso de la
suma de números enteros y recuerdan
la
adición de números naturales y resaltan las
propiedades de este conjunto. (evidenciado a
partir de la aplicación de una prueba
diagnóstica).

5. Aspectos afectivos: Las actitudes y acciones
iníciales de los estudiantes de 7° logran dentro de
ellos unos juicios y unas normatividades que
restringen su desarrollo afectivo hacia el área de
matemáticas, su
núcleo
familiar
no
es
responsable con el compromiso académico
individual o grupal esto es notado en reuniones
de padres o en comunidad.
Aspectos motrices: presentan un nivel positivo en
sus actividades de aprendizaje matemático,
habilidades
para
ejercitar
procesos
de
pensamiento numérico el docente determina a
través de observaciones y desarrollos lúdicos
dentro del aula de clases.

6. Aspectos familiares y socioeconómicos:
en su mayoría pertenecen a grupos
familiares
de
corto
conocimiento
académico, algunos hasta analfabetas
por pertenecer a una región rural, son
familias que dependen mucho de
actividades comerciales como la pesca
y la ganadería; esta característica se
convierte en un aspecto de relevancia
en la asistencia y acompañamiento
personal con los estudiantes.

7. Ambiente Escolar : La Institución Educativa
Agro pesquera Manuel Padilla Polo de robles
presenta un ambiente de armonía es una
planta física acorde al entorno y a su
ubicación geográfica, su característica
principal como rivera del rio Magdalena y su
condición social son cultura propia para el
aprendizaje de cada estudiante.
Dentro de la planta física encontramos
apoyo y recurso educativo por parte de los
docentes, se implementan estrategias
pedagógicas que ayudan a los estudiantes
a construir ideas y comunicación interactiva
que facilitan el aprendizaje de los
estudiantes.

8. Actividades en el Aula: los estudiantes toman sus
apuntes, los directores de grupo hacen el
acompañamiento
constante
motivando
la
participación de los padres de familia sirviendo estos
como orientadores del proceso para cada trabajo
propuesto o actividades de nivelación.
Las herramientas utilizadas con frecuencia para el
aprendizaje con los estudiantes son el tablero y, las
carteleras sirven como apoyo lúdico o didáctico para
el aprendizaje de cada tema a desarrollar.
Los equipos audiovisuales y computadores se han
convertido en una estrategia de poco acceso para
los docentes.

9. DESCRIPCION DEL PROBLEMA
En general se ha detectado en los estudiantes lo
siguiente:
Dificultad al realizar actividades Matemáticas donde
interviene la adición de números enteros,
la
inclusión de situaciones rutinarias y simples.
Análisis y causas:
La
falta de implementación de estrategias de
enseñanzas por parte de los docentes, lo que
permita la apropiación de los conceptos propios
de números enteros.
No tener de referencia los lineamientos curriculares lo
que lleva a la no implementación de estrategias
para el desarrollo del pensamiento numérico y
procedimientos de tipo aritmético.

10. No se desarrollan procesos de habilidad numérica
que
permitan
al
estudiante
viabilizar
su
conocimiento en diferentes contextos de su que
hacer diario.
Consecuencias:
Encontramos un estudiante desmotivado, asumiendo
que la matemática no es una ciencia de
aplicación.
Aprendizaje de los sistemas numéricos resulta difícil
por que no asimila sus conceptos y posibles
aplicaciones.
Rendimiento bajo en pruebas saber, olimpiadas de
matemáticas
y bajo rendimiento en el área en un buen porcentaje
de estudiantes.

11. Los niveles de competencias básicas se
convierten en un arma desafiante para los
estudiantes y esta aversión los desmotiva
cada vez mas por el aprendizaje.
Por ultimo encontramos un estudiante solo
interesado en los resultados de su
evaluación y su formación integral la deja a
un lado.

12. Preguntas
problematizadoras
1. ¿Qué estrategias didácticas sirven para la
comprensión del concepto de números enteros
y los procedimientos para realizar adiciones?
2. ¿Qué situaciones del entorno resultan útiles
para describir adición de números enteros?

13. ELECCION DEL TEMA Y NOMBRE DEL
PROYECTO
ESTRATEGIAS DIDACTICAS PARA EL
APRENDIZAJE DE LA ADICIÓN DE
NÚMEROS ENTEROS En los estudiantes
de 7° de la institución educativa
técnica agro pesquera
Manuel
Padilla Polo de Robles el Guamo
Bolívar

14. JUSTIFICACION
El presente proyecto de aula es pertinente debido a la relevancia del
estudio de los números enteros en el área de matemáticas.
Es un tema especialmente difícil para un grupo de estudiantes del
orden rural hasta ahora acostumbrados a trabajar con números
naturales y números decimales.
Por tanto resulta conveniente implementar estrategias didácticas que
permitan un aprendizaje significativo en torno a al adición de
números enteros.

15. OBJETIVOS
Objetivo general:
-implementar estrategias didácticas que permitan a los
estudiantes de 7° de la Institución Educativa Manuel
Padilla Polo de Robles Bolívar apropiarse de los
conceptos básicos de números enteros y la operación
adición aplicándolos a conceptos cotidianos.
Objetivos específicos:
-Aplicar una prueba diagnostica para determinar el
nivel de manejo de los estudiantes respecto a la
adición con números enteros
-Implementar estrategias didácticas para generar
aprendizaje significativo en torno a al adición con
números enteros.
-revisar los conceptos necesarios para el desarrollo de
contenidos propios de los números enteros.

16. MARCO TEORICO
Para la ejecución del proyecto
de Aula se tendrá en cuenta
lo siguiente:

17. PENSAMIENTO NUMERICO Y SISTEMAS NUMERICOS
Los lineamientos curriculares de matemáticas plantean el
desarrollo de los procesos curriculares y la organización de
actividades centradas en la comprensión del uso y de los
significados de los números y de la numeración; la
comprensión del sentido y significado de las operaciones y las
relaciones entre números, y el desarrollo de diferentes
técnicas de calculo y estimación.

18.  Procesos generales de la actividad matemática:
contemplados en los lineamientos curriculares
1.Formular y resolver problemas
2.Modelar procesos y fenómenos de la realidad
3.Comunicar
4.Razonar
5.Formular,comparar y ejercitar procedimientos y
algoritmos

19. FORMULACION, COMPARACION Y EJERCITACION DE
PROCEDIMIENTOS
proceso que implica comprometer a los estudiantes en la
construcción y ejecución segura de procedimientos mecánicos
o de rutina también llamados algoritmos. Para el análisis en la
ejecución de procedimientos rutinarios en el desarrollo
significativo y comprensivo del conocimiento matemático es
conveniente considerar mecanismos cognoscitivos involucrados
en dichos algoritmos.

20. ADICION DE NUMEROS ENTEROS
NUMERO ENTERO
SUMA DE NUMEROS
POSITIVOS O
NEGATIVOS SIN QUE
TENGAN PARTE
DECIMAL
SUMA DE NUMEROS
DE IGUAL SIGNO
ADICION DE
NUMEROS ENTEROS
-MULTIPLICACION DE
ENTEROS
-DIVISION DE
ENTEROS
SUMA DE NUMEROS
DE DISTINTO SIGNO

21. ESTANDARES BASICOS DE CALIDAD 7°
-Resuelvo problemas cotidianos de suma con números
enteros.
-Establezco conjeturas sobre propiedades y relaciones
de los números enteros utilizando herramientas
tecnológicas.
-Justifico la elección de métodos e instrumentos de
calculo en la resolución de problemas con números
enteros

22. MOMENTOS DEL
AlternaciónAPRENDIZAJE cognoscitivo en los que prima
de momentos: mecanismo
el conocimiento conceptual y el conocimiento procedimental lo
cual requiere de:
-una atención
-un control
-una planeación
-una ejecución y
-una verificación e interpretación intermitente de resultados parciales.

23. MARCO TEORICO
DEFINICIÓN :
Que es la adición de números enteros:
Suma de dos números positivos o negativos
Podemos analizar tres casos:
1.La suma de dos números enteros positivos:
Solo se puede sumar los valores absolutos es decir el numero sin el signo, y su
resultado es positivo.
2.La suma de dos números negativos:
Solo se suman los valores absolutos de ambos números y el resultado es
negativo.

24. 3.La suma de un numero entero positivo mas un numero
entero negativo:
Se restan los valores absolutos y el resultado de la resta
tendrá el signo del numero que cuenta con mayor
valor absoluto.

25. Autores que hablan sobre los procedimientos en
matemáticas:
-Interaprendizaje holístico de matemáticas
Mario Orlando Suarez, (2004)
Un numero entero es cualquier elemento formado por los números naturales
y sus opuestos.
Los números negativos permiten contar nuevos tipos de cantidades, como
los saldos deudores o los pisos de un edificio por encima o por debajo de
la entrada.
Para sumar números enteros de igual signo se suman sus valores absolutos y
al resultado se le pone el signo que tenían los sumandos, es decir signos
iguales se suman y se conserva el signo de los sumandos.

26. -Didáctica de la relatividad Aditivo-Ordinal y de los números
enteros
Mary González, J.P.
“Todas las reglas que se verifican para los números naturales
deben seguir verificándose para los nuevos campos
numéricos de manera que se conserven las definiciones en
el campo menos amplio como casos particulares de las
nuevas definiciones en los campos ampliados sin que exista
contradicción”.

27. -Lúdica y matemáticas a través de las TIC para la practica de
operaciones con la suma de números enteros.
Juan Bautista Valdez,
plantea:
El estudio de sistemas numéricos se les dificulta en el paso del numero
natural al numero entero lo que se manifiesta en la poca asimilación
de estos números con errores de operaciones y relaciones.

28. ESTRATEGIAS
1.Estrategias para entender o interpretar la aparición de números
enteros en situaciones cotidianas:
El estudiantes leerá un texto en el que aparezcan los números
enteros en diferentes situaciones.
A través de estas estrategias se pretende que el estudiante pueda
responder de manera efectiva preguntas como:
-¿Entiende todo lo que esta escrito?
-¿Distingue cuales son los datos?
-¿Hay suficiente información?
-¿Esta ejercitación es igual a otra que haya resuelto antes?

29. El estudiante debe estar preparado para:
-comprender el enunciado (algoritmo)
-interpretar expresiones matemáticas como la adición de
números enteros
-analizar condiciones
-comprender datos
-interpretar un contexto y
-formular preguntas

30. 2.Estrategias para configurar y ejecutar un plan:
Esta estrategia hace referencia al proceso para planear la
secuencia lógica o los pasos procedimentales que utilizara
el estudiante de para resolver algoritmos una vez hayan
entendido.
Uno de los procesos que ayuda a desarrollar esta estrategia es
la modelación, ósea la representación cognitiva interna por
medio de ideogramas escritos u orales.

31. Como tipos de representaciones cognitivas
Goldin (1998) describe las siguientes:
-Manipulación mental de notaciones formales (numerales y
operaciones aritméticas).
-Sistemas de representaciones afectivos, emociones, actitudes,
creencias y valores sobre las matemáticas o sobre si mismas en
relación con las matemáticas.

32. 3. Implementación de las Tics
Implementación de actividades j clic para afianzar los
procedimientos para la adición de números enteros.
http://clic.xtec.cat/db/act_es.jsp?id=3229
http://clic.xtec.cat/db/act_es.jsp?id=1341

33. Como las tic ayudan a los procesos de enseñanza en las
matemáticas.
Se considera implementar ambientes lúdico matemáticos con
las TIC a través del análisis, desarrollo e implementación para
la enseñanza de la operación con adición números enteros,
permitiendo mejorar el razonamiento lógico y la agilidad
mental de los estudiantes de 7° de la IETA Manuel Padilla
Polo de Robles Bolívar.
teniendo en cuenta este análisis, se pretende con esta
herramienta generar ambientes lúdicos matemáticos
incorporando las tecnologías

34. De la información y comunicación que permitan mejorar
los procesos generales que se contemplan en los
lineamientos curriculares de matemáticas pudiendo
concluir que los puntajes o calificaciones que las
calificaciones por los estudiantes a los que se le aplico
la prueba sin las TIC fue inferior al obtenido por los
mismos después de aplicarles estas tecnologías y
volverlos a evaluar teniendo un mejor rendimiento.

35. Se ha venido incrementando el uso de la TIC con ambientes
virtuales para dar solución a problemas prácticos y se ha
observado que los estudiantes se entusiasman y quieren que
se les de mas oportunidades de escrudiñar mas tiempo para
dedicarle a este tipo de material les motiva a ver otras
opciones y observar que las matemáticas se hacen menos
complicadas y son no tan rígidas como se les había hecho
creer con procedimientos que han ido cambiando con el
firme propósito de mejorar.

36. MATERIALES
recursos didácticos y materiales
Los
de trabajo para este
proyecto de aula se señalan a continuación:
-textos guías del grado 7°
-carteleras
-fotocopias
-tablero y marcadores
-computadores para la implementación de las TIC
-actividades en j clic

37. CRONOGRAMA
FECHA
ACTIVIDAD
06-03-2012
Aplicación de la prueba diagnostica
10-04-2012
Retroalimentación
17-04-2012
Actividades de refuerzo
08-05-2012
Reunión con los padres de familia del
grado 7º para plantear la situación
problema.
15-05-2012
Visita a la sala de tecnología e
informática para aplicar las TIC
12-06-2012
Aplicación de evaluación

38. EVALUACION
El decreto 230 de 2002 en su capitulo II refiere que
La evaluación de los estudiantes debe ser continua e integral y
se hará con referencia a cuatro periodos académicos de
igual duración en los que se divide el año escolar.
Objetivos de la evaluación:
-Valorar el alcance y obtención de los logros, competencias y
conocimientos por parte de los estudiantes
-Diseñar e implementar estrategias para apoyar a los
estudiantes que tienen dificultades en el área de estudio.

39. EVALUACION
Se aplica la siguiente evaluación:
Evaluación formativa:
Escribe el numero que falta para que la adición sea correcta:
a) 12+____= -3
f) (-3)+_____= 8
b) ____+3=8
g) _____+(-10)= -17
c) ____+(-7)= -1
h) _____+(-6)
d) 18+____= 23
i) _____+8= 0
e) -15+____= -7
j) 5+____= 2

40. EVALUACION
 Evaluación sumativa:
Encuentra dos números enteros que satisfagan cada condición:
a) dos signos contrarios cuya suma sea 5
b) negativos cuya suma sea -9
c) que la suma sea 0

41. EVALUACION
 Evaluación aplicativa
La siguiente evaluación es aplicada a las pruebas saber y saber icfes:
Si resolvemos la expresión (4+5) – (-9) obtenemos como resultado:
a) 10
b) 0
c) 18
d) 81
A la hora de sumar números enteros se pueden presentar:
a) 2 posibilidades
c) 1 posibilidad
b) 3 posibilidades
d) ninguna de las anteriores

42. Responde las siguientes preguntas:
¿es siempre la adición de números de enteros otro numero
entero? , ¿Por qué?
¿es igual sumar 1 de -2 que -2 de 1?
¿Qué características encuentras al resolver algoritmos con la
suma de números enteros?

43. RESULTADOS
Con relación a la adición de números enteros el porcentaje de
valoración cambio evidenciando una tendencia creciente
al afirmar el grado de verdad de las proposiciones
correspondientes a dicho paradigma.
Este aspecto puede ser interpretado de distintas formas: por
una parte implicaría que las estrategias didacticopedagogicas producen un cambio en la valoración pero
tienden a afirmar el paradigma dominante. En ese mismo
orden de ideas, el hecho podría significar que las
estrategias favorecen a que los estudiantes de 7° de la IETA
Manuel Padilla Polo de Robles

44. Tomen conciencia de los referentes epistemológicos que
los constituyen pero no incorporan un dispositivo
critico que les permita tomar distancia de los mismos.
Por ultimo, podría significar también que para los
estudiantes y el profesor el cambio no tiene una
dirección especifica hacia el tema en particular sino
hacia el reconocimiento y construcción de ideas para
un análisis de procesos de calculo aritmético.

45. BIBLIOGRAFIA
-Estándares básicos de calidad
Área de matemática
-Ley general de educación
Ley 115 de febrero 8 de 1994
-Lineamientos curriculares de matemáticas
Ministerio de Educación Nacional
-Teorías cognitivas del Aprendizaje J.L. Pozo (1989) Madrid
Morata
-Unidades didácticas en ciencias y matemáticas
Digna Couso-Edelmira Badillo Editorial Magisterio
-Misión Matemática 7°
Fabián Martínez - Norely Useche
Editorial Educar

46. ANEXOS

47.  Institución educativa Manuel Padilla Polo de Robles Bolívar.
Prueba diagnostica 7º grado Jornada: diurna
Nombre del estudiante
Nombre del docente: Lic. Luis F. González
I periodo académico 2012

48. PRUEBA DIAGNOSTICA:
Elaborar suma con números enteros:
7+2-3=(7+2)-3
= 9-3
=
se suman 7 y 2
se restan 9 y 3
6
(2-1)-(2+5)=1-(2+5) se restan 2 y 1
=1-7
se suman 2 y 5
=-6
se restan 1 y 7

49. -(-3-5)-(-2-7)= -(-8)-(-2-7) se suman -3 y -5
=-(-8)-(-9)
se suman -2 y -7
=+8+9
se distribuye el signo-
= 17
se suman 8 y 9
-(4+7)-(6-1)= -11-(6-1) se suman 4 y 7
= -11-5
se restan 6 y 1
= -16
se suman -11y -5

50. histograma
Para una muestra n= 48, el numero de estudiantes del
grado 7º de la I.E.T.A. Manuel Padilla Polo de Robles
Bolívar, partir de la prueba diagnostico se pudo
interpretar con un diagrama de barras o histograma
donde se arrojan los resultados.

51. Nº de estudiantes
histograma
calificación

52. EVIDENCIA
 Estudiantes de grado 7º con dificultades en el aprendizaje
de matemáticas.

53. RESUTADOS DE LA PRUEBA
DIAGNOSTICA

54. ACTIVIDADES
Actividad 1:
Aplicar la propiedad asociativa de los números
naturales para los siguientes sumandos:
3+5+7
Desarrollo: 3+5+7= 3+(5+7)= (3+5)+7
El estudiante demuestra a través del pensamiento
numérico la solución de una suma de varios
sumandos agrupando los números en diferente
orden.

55. ACTIVIDADES
Actividad 2:
¿Qué notas al observar las siguientes propiedades
de la suma de números naturales?
a) 3+2=2+3
b) 5+0=0+5=5
c) 8+(7+5)=(8+7)+5
Un estudiante responde, las tres propiedades
anteriores son diferentes otro responde hay dos
propiedades que me generan el mismo resultado y
al finalizar la discusión de posibles respuestas ya
encontramos un estudiante centrado en la
temática que se esta desarrollando.

56. Actividad 3: ¿Tienes o debes dinero?
Que significa la expresión:
a) -6+8
Puede ser tengo 8 pollitos pero debo 6 pollitos en realidad tienes
2 pollitos
b) -7-5
Debo 7 libras de maíz y tengo una deuda de 5 libras por tanto en
total acumulo una deuda de 12 libas de maíz lo que es -12 libras

57. c) +6+3
Tengo 6 naranjas y adiciono 3 mangos en total tengo 9
frutas
d)+3-5
Debo 5 chivos y tengo 3 chivos por tanto puedo pagar
una parte de la deuda de los chivos pero no la puedo
pagar completa por lo tanto aun debo, lo que es -2
chivos