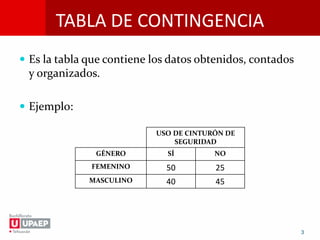
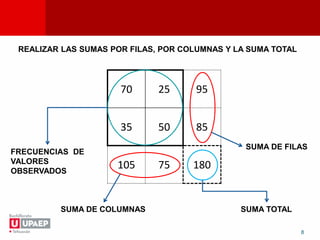
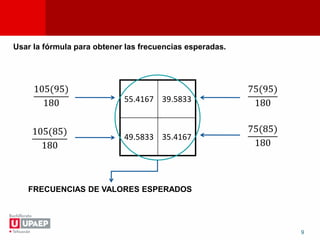
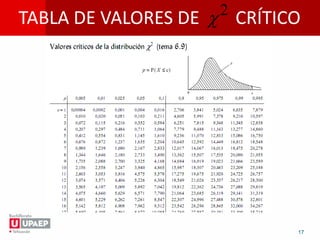
La prueba chi-cuadrada determina si dos variables están relacionadas. Se formula una hipótesis nula y alternativa, se calculan las frecuencias esperadas y el chi-cuadrado observado, y se compara con el valor crítico de la tabla para aceptar o rechazar la hipótesis nula. El documento provee los pasos para realizar la prueba chi-cuadrada y un ejemplo sobre la relación entre el uso de cinturón de seguridad y el género.