Este documento presenta una introducción al modelo de regresión lineal simple. Explica que la regresión lineal estudia la dependencia entre una variable dependiente (Y) y una variable independiente (X). Define el modelo de regresión lineal simple como Y = β0 + β1X1 + ε, donde β0 y β1 son parámetros a estimar y ε es el error aleatorio. Finalmente, indica que el objetivo es determinar si existe una relación lineal significativa entre las variables.

1. Undécima sección
Regresión lineal simple
MSc. Edgar Madrid Cuello.
Dpto de Matemática, UNISUCRE
Análisis y diseño de experimentos
Julio 2019
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

2. Undécima sección
Generalidades
Denición
Uno de los aspectos más relevantes de la Estadística es el análisis
de la relación o dependencia entre variables. Frecuentemente
resulta de interés conocer el efecto que una o varias variables
pueden causar sobre otra, e incluso predecir en mayor o menor
grado valores en una variable a partir de otra.
Los métodos de regresión estudian la construcción de modelos para
explicar o representar la dependencia entre una variable respuesta o
dependiente (Y ) y la(s) variable(s) explicativa(s) o
independiente(s), X.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

3. Undécima sección
Generalidades
Denición
Uno de los aspectos más relevantes de la Estadística es el análisis
de la relación o dependencia entre variables. Frecuentemente
resulta de interés conocer el efecto que una o varias variables
pueden causar sobre otra, e incluso predecir en mayor o menor
grado valores en una variable a partir de otra.
Los métodos de regresión estudian la construcción de modelos para
explicar o representar la dependencia entre una variable respuesta o
dependiente (Y ) y la(s) variable(s) explicativa(s) o
independiente(s), X.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

4. Undécima sección
Generalidades
Denición
Uno de los aspectos más relevantes de la Estadística es el análisis
de la relación o dependencia entre variables. Frecuentemente
resulta de interés conocer el efecto que una o varias variables
pueden causar sobre otra, e incluso predecir en mayor o menor
grado valores en una variable a partir de otra.
Los métodos de regresión estudian la construcción de modelos para
explicar o representar la dependencia entre una variable respuesta o
dependiente (Y ) y la(s) variable(s) explicativa(s) o
independiente(s), X.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

5. Undécima sección
Generalidades
Denición
En este tema abordaremos el modelo de regresión lineal, que tiene
lugar cuando la dependencia es de tipo lineal, y daremos respuesta
a dos cuestiones básicas:
¾Es signicativo el efecto que una variable X causa sobre otra
Y ? ¾Es signicativa la dependencia lineal entre esas dos
variables?.
De ser así, utilizaremos el modelo de regresión lineal simple
para explicar y predecir la variable dependiente (Y ) a partir de
valores observados en la independiente (X).
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

6. Undécima sección
Generalidades
Denición
En este tema abordaremos el modelo de regresión lineal, que tiene
lugar cuando la dependencia es de tipo lineal, y daremos respuesta
a dos cuestiones básicas:
¾Es signicativo el efecto que una variable X causa sobre otra
Y ? ¾Es signicativa la dependencia lineal entre esas dos
variables?.
De ser así, utilizaremos el modelo de regresión lineal simple
para explicar y predecir la variable dependiente (Y ) a partir de
valores observados en la independiente (X).
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

7. Undécima sección
Generalidades
Denición
En este tema abordaremos el modelo de regresión lineal, que tiene
lugar cuando la dependencia es de tipo lineal, y daremos respuesta
a dos cuestiones básicas:
¾Es signicativo el efecto que una variable X causa sobre otra
Y ? ¾Es signicativa la dependencia lineal entre esas dos
variables?.
De ser así, utilizaremos el modelo de regresión lineal simple
para explicar y predecir la variable dependiente (Y ) a partir de
valores observados en la independiente (X).
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

8. Undécima sección
Generalidades
Denición
La forma de la función es desconocida para el investigador, pero en
muchos casos puede suponerse una función polinómica de la forma:
Y = β0 + β1X1 + . . . + βpXp (1)
Cuando se considera una sola variable explicativa, la función tiene
la forma:
Y = β0 + β1X1 (2)
Las ecuaciones 1 y 2 representan modelos determinísticos para la
variable dependiente. Si se desea analizar una relación estadística
entre las variables, es necesario agregar una componente aleatoria ε
para denotar el error de medición en la variable de respuesta.
Entonces, el modelo estadístico puede escribirse como;
Y = β0 + β1X1 + ε (3)
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

9. Undécima sección
Generalidades
Denición
La forma de la función es desconocida para el investigador, pero en
muchos casos puede suponerse una función polinómica de la forma:
Y = β0 + β1X1 + . . . + βpXp (1)
Cuando se considera una sola variable explicativa, la función tiene
la forma:
Y = β0 + β1X1 (2)
Las ecuaciones 1 y 2 representan modelos determinísticos para la
variable dependiente. Si se desea analizar una relación estadística
entre las variables, es necesario agregar una componente aleatoria ε
para denotar el error de medición en la variable de respuesta.
Entonces, el modelo estadístico puede escribirse como;
Y = β0 + β1X1 + ε (3)
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

10. Undécima sección
Generalidades
Denición
La forma de la función es desconocida para el investigador, pero en
muchos casos puede suponerse una función polinómica de la forma:
Y = β0 + β1X1 + . . . + βpXp (1)
Cuando se considera una sola variable explicativa, la función tiene
la forma:
Y = β0 + β1X1 (2)
Las ecuaciones 1 y 2 representan modelos determinísticos para la
variable dependiente. Si se desea analizar una relación estadística
entre las variables, es necesario agregar una componente aleatoria ε
para denotar el error de medición en la variable de respuesta.
Entonces, el modelo estadístico puede escribirse como;
Y = β0 + β1X1 + ε (3)
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

11. Undécima sección
Generalidades
Denición
La forma de la función es desconocida para el investigador, pero en
muchos casos puede suponerse una función polinómica de la forma:
Y = β0 + β1X1 + . . . + βpXp (1)
Cuando se considera una sola variable explicativa, la función tiene
la forma:
Y = β0 + β1X1 (2)
Las ecuaciones 1 y 2 representan modelos determinísticos para la
variable dependiente. Si se desea analizar una relación estadística
entre las variables, es necesario agregar una componente aleatoria ε
para denotar el error de medición en la variable de respuesta.
Entonces, el modelo estadístico puede escribirse como;
Y = β0 + β1X1 + ε (3)
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

12. Undécima sección
Generalidades
Denición
La forma de la función es desconocida para el investigador, pero en
muchos casos puede suponerse una función polinómica de la forma:
Y = β0 + β1X1 + . . . + βpXp (1)
Cuando se considera una sola variable explicativa, la función tiene
la forma:
Y = β0 + β1X1 (2)
Las ecuaciones 1 y 2 representan modelos determinísticos para la
variable dependiente. Si se desea analizar una relación estadística
entre las variables, es necesario agregar una componente aleatoria ε
para denotar el error de medición en la variable de respuesta.
Entonces, el modelo estadístico puede escribirse como;
Y = β0 + β1X1 + ε (3)
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

13. Undécima sección
Generalidades
Denición
La forma de la función es desconocida para el investigador, pero en
muchos casos puede suponerse una función polinómica de la forma:
Y = β0 + β1X1 + . . . + βpXp (1)
Cuando se considera una sola variable explicativa, la función tiene
la forma:
Y = β0 + β1X1 (2)
Las ecuaciones 1 y 2 representan modelos determinísticos para la
variable dependiente. Si se desea analizar una relación estadística
entre las variables, es necesario agregar una componente aleatoria ε
para denotar el error de medición en la variable de respuesta.
Entonces, el modelo estadístico puede escribirse como;
Y = β0 + β1X1 + ε (3)
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

14. Undécima sección
Generalidades
Denición
La forma de la función es desconocida para el investigador, pero en
muchos casos puede suponerse una función polinómica de la forma:
Y = β0 + β1X1 + . . . + βpXp (1)
Cuando se considera una sola variable explicativa, la función tiene
la forma:
Y = β0 + β1X1 (2)
Las ecuaciones 1 y 2 representan modelos determinísticos para la
variable dependiente. Si se desea analizar una relación estadística
entre las variables, es necesario agregar una componente aleatoria ε
para denotar el error de medición en la variable de respuesta.
Entonces, el modelo estadístico puede escribirse como;
Y = β0 + β1X1 + ε (3)
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

15. Undécima sección
Generalidades
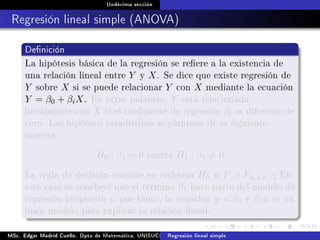
Denición
El término regresión se debe a Francis Galton, quien lo uso por
primera vez en una publicación en 1885 sobre las leyes de la
herencia (Regression towards mediocrity in hereditary stature).
En sus investigaciones encontró que algunas características de los
hijos se asemejaban a las de los padres pero regresaban, en cierta
medida, a los estándares de la raza. Así, si los padres son altos, los
hijos también tienden a serlo, aunque su estatura está más ajustada
al promedio de la raza, o sea, regresa o retrocede al estándar.
Igualmente, los hijos de padres de baja estatura tienden a ser bajos.
[1]
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

16. Undécima sección
Generalidades
Denición
Una forma de determinar si puede existir o no dependencia entre
variables, y en caso de haberla deducir de qué tipo puede ser, es
grácamente representando los pares de valores observados. A
dicho gráco se le llama nube de puntos o diagrama de dispersión.
independencia
hay ausencia de relación
positiva
existe asociación lineal positiva
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

17. Undécima sección
Generalidades
Denición
Una forma de determinar si puede existir o no dependencia entre
variables, y en caso de haberla deducir de qué tipo puede ser, es
grácamente representando los pares de valores observados. A
dicho gráco se le llama nube de puntos o diagrama de dispersión.
independencia
hay ausencia de relación
positiva
existe asociación lineal positiva
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

18. Undécima sección
Generalidades
Denición
Una forma de determinar si puede existir o no dependencia entre
variables, y en caso de haberla deducir de qué tipo puede ser, es
grácamente representando los pares de valores observados. A
dicho gráco se le llama nube de puntos o diagrama de dispersión.
independencia
hay ausencia de relación
positiva
existe asociación lineal positiva
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

19. Undécima sección
Generalidades
Denición
Una forma de determinar si puede existir o no dependencia entre
variables, y en caso de haberla deducir de qué tipo puede ser, es
grácamente representando los pares de valores observados. A
dicho gráco se le llama nube de puntos o diagrama de dispersión.
independencia
hay ausencia de relación
positiva
existe asociación lineal positiva
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

20. Undécima sección
Generalidades
Denición
negativa
existe asociación lineal negativa
no lineal
existe fuerte asociación, pero no
lineal.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

21. Undécima sección
Generalidades
Denición
negativa
existe asociación lineal negativa
no lineal
existe fuerte asociación, pero no
lineal.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

22. Undécima sección
Generalidades
Denición
negativa
existe asociación lineal negativa
no lineal
existe fuerte asociación, pero no
lineal.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

23. Undécima sección
Regresión lineal simple
Denición
La estructura del modelo de regresión lineal es la siguiente:
Y = β0 + β1X1 + ε (4)
En términos de los valores observados, el modelo de regresión se
representa de esta forma:
yi = β0 + βxi con i = 1, 2, . . . , n (5)
Las inferencias en regresión simple se basan en cuatro supuestos.
Estos son:
1 La variable explicativa X se mide sin error, es decir, está bajo
el control del investigador quien escoge los valores sin las
inuencias del azar.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

24. Undécima sección
Regresión lineal simple
Denición
La estructura del modelo de regresión lineal es la siguiente:
Y = β0 + β1X1 + ε (4)
En términos de los valores observados, el modelo de regresión se
representa de esta forma:
yi = β0 + βxi con i = 1, 2, . . . , n (5)
Las inferencias en regresión simple se basan en cuatro supuestos.
Estos son:
1 La variable explicativa X se mide sin error, es decir, está bajo
el control del investigador quien escoge los valores sin las
inuencias del azar.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

25. Undécima sección
Regresión lineal simple
Denición
La estructura del modelo de regresión lineal es la siguiente:
Y = β0 + β1X1 + ε (4)
En términos de los valores observados, el modelo de regresión se
representa de esta forma:
yi = β0 + βxi con i = 1, 2, . . . , n (5)
Las inferencias en regresión simple se basan en cuatro supuestos.
Estos son:
1 La variable explicativa X se mide sin error, es decir, está bajo
el control del investigador quien escoge los valores sin las
inuencias del azar.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

26. Undécima sección
Regresión lineal simple
Denición
1 La relación entre los valores esperados de Y y los valores de X
puede expresarse mediante una función lineal.
2 Los diferentes valores de Y para cada valor de X son
independientes y tienen distribución Normal. Otra forma de
describir este supuesto es exigir que los errores ε, sean
probabilísticamente independientes y con distribución N(0, σ2)
para cada valor de X.
3 Los errores ε tienen varianzas homogéneas para cada valor de
X, o sea que la varianza en torno a la línea de regresión es
constante y no depende del valor que tome X. [1]
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

27. Undécima sección
Estimación de los parámetros del modelo
Denición
Partimos de una muestra de valores de x e y medidos sobre n
individuos:
(x1, y1) , (x2, y2) , . . . (xn, yn) (6)
y queremos estimar valores en Y según el modelo Y = β0 + β1X
donde β0 y β1 son por el momento desconocidos. Debemos
encontrar entonces de entre todas las rectas la que mejor se ajuste
a los datos observados, es decir, buscamos aquellos valores de β0 y
β1 que hagan mínimos los errores de estimación. Para un valor xi
el modelo estima un valor en Y igual a yi = β0 + β1xi y el valor
observado en Y es igual a yi, con lo cual el error de estimación (o
residuo) en ese caso vendría dado por ei = yi − yi = yi − β0 − β1xi
.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

28. Undécima sección
Estimación de los parámetros del modelo
Denición
Partimos de una muestra de valores de x e y medidos sobre n
individuos:
(x1, y1) , (x2, y2) , . . . (xn, yn) (6)
y queremos estimar valores en Y según el modelo Y = β0 + β1X
donde β0 y β1 son por el momento desconocidos. Debemos
encontrar entonces de entre todas las rectas la que mejor se ajuste
a los datos observados, es decir, buscamos aquellos valores de β0 y
β1 que hagan mínimos los errores de estimación. Para un valor xi
el modelo estima un valor en Y igual a yi = β0 + β1xi y el valor
observado en Y es igual a yi, con lo cual el error de estimación (o
residuo) en ese caso vendría dado por ei = yi − yi = yi − β0 − β1xi
.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

29. Undécima sección
Estimación de los parámetros del modelo
Denición
Entonces tomaremos como estimaciones de β0 y β1 que notamos
por β0 y β1 aquellos valores que hagan mínima la suma de los
errores al cuadrado, que viene dada por:
SSE =
i
e2
i =
i
(yi − β0 − β1xi)2
(7)
De ahí que al método de estimación se le llame método de mínimos
cuadrados. La solución se obtiene por el mecanismo habitual,
derivando SSE con respecto a β0 y β1 e igualando a 0. Los
estimadores resultan:
β1 =
Sxy
Sxx
y β0 = ¯y − β1¯x (8)
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

30. Undécima sección
Estimación de los parámetros del modelo
Denición
Entonces tomaremos como estimaciones de β0 y β1 que notamos
por β0 y β1 aquellos valores que hagan mínima la suma de los
errores al cuadrado, que viene dada por:
SSE =
i
e2
i =
i
(yi − β0 − β1xi)2
(7)
De ahí que al método de estimación se le llame método de mínimos
cuadrados. La solución se obtiene por el mecanismo habitual,
derivando SSE con respecto a β0 y β1 e igualando a 0. Los
estimadores resultan:
β1 =
Sxy
Sxx
y β0 = ¯y − β1¯x (8)
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

31. Undécima sección
Estimación de los parámetros del modelo
Denición
Entonces tomaremos como estimaciones de β0 y β1 que notamos
por β0 y β1 aquellos valores que hagan mínima la suma de los
errores al cuadrado, que viene dada por:
SSE =
i
e2
i =
i
(yi − β0 − β1xi)2
(7)
De ahí que al método de estimación se le llame método de mínimos
cuadrados. La solución se obtiene por el mecanismo habitual,
derivando SSE con respecto a β0 y β1 e igualando a 0. Los
estimadores resultan:
β1 =
Sxy
Sxx
y β0 = ¯y − β1¯x (8)
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

32. Undécima sección
Estimación de los parámetros del modelo
Denición
Entonces tomaremos como estimaciones de β0 y β1 que notamos
por β0 y β1 aquellos valores que hagan mínima la suma de los
errores al cuadrado, que viene dada por:
SSE =
i
e2
i =
i
(yi − β0 − β1xi)2
(7)
De ahí que al método de estimación se le llame método de mínimos
cuadrados. La solución se obtiene por el mecanismo habitual,
derivando SSE con respecto a β0 y β1 e igualando a 0. Los
estimadores resultan:
β1 =
Sxy
Sxx
y β0 = ¯y − β1¯x (8)
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

33. Undécima sección
Estimación de los parámetros del modelo
Denición
Entonces tomaremos como estimaciones de β0 y β1 que notamos
por β0 y β1 aquellos valores que hagan mínima la suma de los
errores al cuadrado, que viene dada por:
SSE =
i
e2
i =
i
(yi − β0 − β1xi)2
(7)
De ahí que al método de estimación se le llame método de mínimos
cuadrados. La solución se obtiene por el mecanismo habitual,
derivando SSE con respecto a β0 y β1 e igualando a 0. Los
estimadores resultan:
β1 =
Sxy
Sxx
y β0 = ¯y − β1¯x (8)
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

34. Undécima sección
Estimación de los parámetros del modelo
Denición
donde
Sxx = x2
i − 1
n ( xi)2
Syy = y2
i − 1
n ( yi)2
Sxy = xiyi − 1
n ( xi) ( yi)
(9)
A la recta resultante Y = β0 + β1X1 se le llama recta de regresión
lineal de Y sobre X.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

35. Undécima sección
Regresión lineal simple
Denición
De otro lado, el modelo de regresión lineal simple es una ecuación
de primer grado en X que puede representarse grácamente con
una línea recta en el plano cartesiano.
Si el modelo postulado es correcto, es decir, si la recta poblacional
representa la verdadera relación entre las variables, la recta
ajustada deberá ser similar a la poblacional o teórica y ei ≈ εi para
todo i. Para determinar si la recta estimada tiene buena precisión,
esto es, si está cerca de la recta verdadera en la población, la
estadística supone que los datos para la regresión se obtuvieron
aleatoriamente, sin sesgos y sin errores sistemáticos.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

36. Undécima sección
Regresión lineal simple
Denición
De otro lado, el modelo de regresión lineal simple es una ecuación
de primer grado en X que puede representarse grácamente con
una línea recta en el plano cartesiano.
Si el modelo postulado es correcto, es decir, si la recta poblacional
representa la verdadera relación entre las variables, la recta
ajustada deberá ser similar a la poblacional o teórica y ei ≈ εi para
todo i. Para determinar si la recta estimada tiene buena precisión,
esto es, si está cerca de la recta verdadera en la población, la
estadística supone que los datos para la regresión se obtuvieron
aleatoriamente, sin sesgos y sin errores sistemáticos.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

37. Undécima sección
Regresión lineal simple
Denición
De otro lado, el modelo de regresión lineal simple es una ecuación
de primer grado en X que puede representarse grácamente con
una línea recta en el plano cartesiano.
Si el modelo postulado es correcto, es decir, si la recta poblacional
representa la verdadera relación entre las variables, la recta
ajustada deberá ser similar a la poblacional o teórica y ei ≈ εi para
todo i. Para determinar si la recta estimada tiene buena precisión,
esto es, si está cerca de la recta verdadera en la población, la
estadística supone que los datos para la regresión se obtuvieron
aleatoriamente, sin sesgos y sin errores sistemáticos.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

38. Undécima sección
Regresión lineal simple
Denición (...Continuación)
Se trata, entonces, de estimar la precisión de la recta ajustada
mediante una medida de variabilidad; la más indicada es la varianza
de los residuos ei y mientras más pequeña sea esta varianza mejor
es el ajuste. Grácamente, el ajuste es mejor mientras más cerca
estén los puntos observados de la recta de regresión.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

39. Undécima sección
Regresión lineal simple (ANOVA)
Denición
De otro lado, la calidad del ajuste de una recta de regresión se mide
por la varianza residual σ2 y esta se estima mediante la MCE del
ANOVA de regresión. Como el modelo de regresión es también un
modelo lineal, se puede usar la técnica del ANOVA para estimar la
varianza y probar la hipótesis de regresión. La variabilidad en Y
dada por SCT = (yi − ¯y)2 puede subdividirse en dos
componentes: una, explicada por la relación de Y con X, llamada
suma de cuadrados debida a la regresión, SCR = (yi − ¯y)2 y la
suma de cuadrados del error aleatorio, llamada suma de cuadrados
alrededor de la regresión SCE = (yi − yi)2.Esta última suma se
origina porque no todos los puntos observados caen sobre la recta
de regresión. Cada suma de cuadrados tiene asociado su propio
número de gl, correspondiente al ANOVA para la regresión lineal
simple.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

40. Undécima sección
Regresión lineal simple (ANOVA)
Denición
De otro lado, la calidad del ajuste de una recta de regresión se mide
por la varianza residual σ2 y esta se estima mediante la MCE del
ANOVA de regresión. Como el modelo de regresión es también un
modelo lineal, se puede usar la técnica del ANOVA para estimar la
varianza y probar la hipótesis de regresión. La variabilidad en Y
dada por SCT = (yi − ¯y)2 puede subdividirse en dos
componentes: una, explicada por la relación de Y con X, llamada
suma de cuadrados debida a la regresión, SCR = (yi − ¯y)2 y la
suma de cuadrados del error aleatorio, llamada suma de cuadrados
alrededor de la regresión SCE = (yi − yi)2.Esta última suma se
origina porque no todos los puntos observados caen sobre la recta
de regresión. Cada suma de cuadrados tiene asociado su propio
número de gl, correspondiente al ANOVA para la regresión lineal
simple.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

41. Undécima sección
Regresión lineal simple (ANOVA)
Denición
De otro lado, la calidad del ajuste de una recta de regresión se mide
por la varianza residual σ2 y esta se estima mediante la MCE del
ANOVA de regresión. Como el modelo de regresión es también un
modelo lineal, se puede usar la técnica del ANOVA para estimar la
varianza y probar la hipótesis de regresión. La variabilidad en Y
dada por SCT = (yi − ¯y)2 puede subdividirse en dos
componentes: una, explicada por la relación de Y con X, llamada
suma de cuadrados debida a la regresión, SCR = (yi − ¯y)2 y la
suma de cuadrados del error aleatorio, llamada suma de cuadrados
alrededor de la regresión SCE = (yi − yi)2.Esta última suma se
origina porque no todos los puntos observados caen sobre la recta
de regresión. Cada suma de cuadrados tiene asociado su propio
número de gl, correspondiente al ANOVA para la regresión lineal
simple.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

42. Undécima sección
Regresión lineal simple (ANOVA)
Denición
De otro lado, la calidad del ajuste de una recta de regresión se mide
por la varianza residual σ2 y esta se estima mediante la MCE del
ANOVA de regresión. Como el modelo de regresión es también un
modelo lineal, se puede usar la técnica del ANOVA para estimar la
varianza y probar la hipótesis de regresión. La variabilidad en Y
dada por SCT = (yi − ¯y)2 puede subdividirse en dos
componentes: una, explicada por la relación de Y con X, llamada
suma de cuadrados debida a la regresión, SCR = (yi − ¯y)2 y la
suma de cuadrados del error aleatorio, llamada suma de cuadrados
alrededor de la regresión SCE = (yi − yi)2.Esta última suma se
origina porque no todos los puntos observados caen sobre la recta
de regresión. Cada suma de cuadrados tiene asociado su propio
número de gl, correspondiente al ANOVA para la regresión lineal
simple.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

43. Undécima sección
Regresión lineal simple (ANOVA)
Denición
F de variación SC df MC MCesperada F
Debida a la regre-
sión (modelo)
SCR 1 MCR σ2 + β1Sxx
MCR
MCE
Alrededor de la
regresión (error
aleatorio)
SCE n − 2 MCE σ2
Total SCT n − 1
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

44. Undécima sección
Regresión lineal simple (ANOVA)
Denición
La hipótesis básica de la regresión se reere a la existencia de
una relación lineal entre Y y X. Se dice que existe regresión de
Y sobre X si se puede relacionar Y con X mediante la ecuación
Y = β0 + βiX. En otras palabras, Y está relacionada
linealmente con X si el coeciente de regresión βi es diferente de
cero. Las hipótesis estadísticas se plantean de la siguiente
manera:
H0 : β1 = 0 contra H1 : β1 = 0
La regla de decisión consiste en rechazar H0 si F ≥ Fα,1,n−2 En
este caso se concluye que el término β1 hace parte del modelo de
regresión propuesto y, por tanto, la ecuación y = β0 + β1x es un
buen modelo para explicar la relación lineal.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

45. Undécima sección
Regresión lineal simple (ANOVA)
Denición
La hipótesis básica de la regresión se reere a la existencia de
una relación lineal entre Y y X. Se dice que existe regresión de
Y sobre X si se puede relacionar Y con X mediante la ecuación
Y = β0 + βiX. En otras palabras, Y está relacionada
linealmente con X si el coeciente de regresión βi es diferente de
cero. Las hipótesis estadísticas se plantean de la siguiente
manera:
H0 : β1 = 0 contra H1 : β1 = 0
La regla de decisión consiste en rechazar H0 si F ≥ Fα,1,n−2 En
este caso se concluye que el término β1 hace parte del modelo de
regresión propuesto y, por tanto, la ecuación y = β0 + β1x es un
buen modelo para explicar la relación lineal.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

46. Undécima sección
Regresión lineal simple (ANOVA)
Denición
La hipótesis básica de la regresión se reere a la existencia de
una relación lineal entre Y y X. Se dice que existe regresión de
Y sobre X si se puede relacionar Y con X mediante la ecuación
Y = β0 + βiX. En otras palabras, Y está relacionada
linealmente con X si el coeciente de regresión βi es diferente de
cero. Las hipótesis estadísticas se plantean de la siguiente
manera:
H0 : β1 = 0 contra H1 : β1 = 0
La regla de decisión consiste en rechazar H0 si F ≥ Fα,1,n−2 En
este caso se concluye que el término β1 hace parte del modelo de
regresión propuesto y, por tanto, la ecuación y = β0 + β1x es un
buen modelo para explicar la relación lineal.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

47. Undécima sección
Ejemplo
Se requiere conocer la relación entre la concentración de una
sustancia y su densidad óptica. La variable independiente X es la
concentración, la cual se tomó a diferentes niveles desde 80 hasta
520 ppm. La variable de respuesta Y representa unidades de
densidad óptica, DO, medidas para cada una de las
concentraciones. Se tienen los siguientes datosa:
Conc. X: 80 120 160 200 240 280 320 360
DO Y: 0.08 0.12 0.18 0.21 0.28 0.28 0.38 0.4
Conc. X: 400 440 480 520
DO Y: 0.42 0.5 0.52 0.6
a
Tomado de:Diseño estadístico de experimentos, Abel Díaz, 2a edición
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

48. Undécima sección
Ejemplo
100 200 300 400 500
0.10.20.30.40.50.6
Regresión simple
Concentración vs. OD
Concentración ppm
Densidadóptica
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

49. Undécima sección
Ejemplo
100 200 300 400 500
0.10.20.30.40.50.6
Regresión simple
Concentración vs. OD
Concentración ppm
Densidadóptica
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

50. Undécima sección
Ejemplo
β1 =
Sxy
Sxx
β0 = ¯y − β1¯x
Sxx = x2
i −
1
n
( xi)2
Syy = y2
i −
1
n
( yi)2
Sxy = xiyi −
1
n
( xi) ( yi)
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

51. Undécima sección
Ejemplo
β1 =
Sxy
Sxx
β0 = ¯y − β1¯x
Sxx = x2
i −
1
n
( xi)2
Syy = y2
i −
1
n
( yi)2
Sxy = xiyi −
1
n
( xi) ( yi)
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

52. Undécima sección
Ejemplo
SCT = Syy =
SCR =
S2
xy
Sxx
=
SCE = SCT − SCR
La variación de la DO está asociada a los niveles de concentración
de la sustancia. Esta asociación o dependencia se mide con el
coeciente de determinación R2denido como:
Denición (coeciente de determinación)
R2
=
SCT − SCE
SCT
(10)
Este coeciente mide la reducción proporcional de la varianza total
en y al usar el estimador y en vez de ¯y para estimar valores de Y
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

53. Undécima sección
Ejemplo
SCT = Syy =
SCR =
S2
xy
Sxx
=
SCE = SCT − SCR
La variación de la DO está asociada a los niveles de concentración
de la sustancia. Esta asociación o dependencia se mide con el
coeciente de determinación R2denido como:
Denición (coeciente de determinación)
R2
=
SCT − SCE
SCT
(10)
Este coeciente mide la reducción proporcional de la varianza total
en y al usar el estimador y en vez de ¯y para estimar valores de Y
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

54. Undécima sección
Ejemplo
SCT = Syy =
SCR =
S2
xy
Sxx
=
SCE = SCT − SCR
La variación de la DO está asociada a los niveles de concentración
de la sustancia. Esta asociación o dependencia se mide con el
coeciente de determinación R2denido como:
Denición (coeciente de determinación)
R2
=
SCT − SCE
SCT
(10)
Este coeciente mide la reducción proporcional de la varianza total
en y al usar el estimador y en vez de ¯y para estimar valores de Y
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

55. Undécima sección
Ejemplo
Un valor alto de R2 no indica que la relación de Y con X sea
necesariamente lineal, es decir, no implica que X sea un buen
predictor lineal de Y , solo que hay mayor precisión en la estimación
de Y si se tiene en cuenta la variable X que si no se tiene en
cuenta, Anderson-Sprecher (1994).
El coeciente R2 aumenta con el espaciamiento de los valores de X
aunque el ajuste lineal no sea bueno. Por otra parte, R2 ≈ 0 puede
indicar que no hay dependencia lineal de Y con X o que la
dependencia es no lineal. Así, R2 no mide idoneidad del modelo
lineal.
Denición
Coeciente de correlación Mide la intensidad de la relación lineal
entre dos variables, se obtiene de la siguiente manera:
r =
Sxy
SxxSyy
(11)
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

56. Undécima sección
Ejemplo
Un valor alto de R2 no indica que la relación de Y con X sea
necesariamente lineal, es decir, no implica que X sea un buen
predictor lineal de Y , solo que hay mayor precisión en la estimación
de Y si se tiene en cuenta la variable X que si no se tiene en
cuenta, Anderson-Sprecher (1994).
El coeciente R2 aumenta con el espaciamiento de los valores de X
aunque el ajuste lineal no sea bueno. Por otra parte, R2 ≈ 0 puede
indicar que no hay dependencia lineal de Y con X o que la
dependencia es no lineal. Así, R2 no mide idoneidad del modelo
lineal.
Denición
Coeciente de correlación Mide la intensidad de la relación lineal
entre dos variables, se obtiene de la siguiente manera:
r =
Sxy
SxxSyy
(11)
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

57. Undécima sección
Ejemplo
Un valor alto de R2 no indica que la relación de Y con X sea
necesariamente lineal, es decir, no implica que X sea un buen
predictor lineal de Y , solo que hay mayor precisión en la estimación
de Y si se tiene en cuenta la variable X que si no se tiene en
cuenta, Anderson-Sprecher (1994).
El coeciente R2 aumenta con el espaciamiento de los valores de X
aunque el ajuste lineal no sea bueno. Por otra parte, R2 ≈ 0 puede
indicar que no hay dependencia lineal de Y con X o que la
dependencia es no lineal. Así, R2 no mide idoneidad del modelo
lineal.
Denición
Coeciente de correlación Mide la intensidad de la relación lineal
entre dos variables, se obtiene de la siguiente manera:
r =
Sxy
SxxSyy
(11)
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

58. Undécima sección
Estimación de los parámetros de la regresión
Denición
En el análisis de regresión lineal simple se tienen como parámetros
fundamentales los coecientes β0 y β1, la varianza σ2 del error y el
valor medio de Y para un X dado µy.x. Sus estimaciones
puntuales, considerando el ejemplo anterior, son:
1 β0 = β0 =
representa el intercepto de la recta sobre el eje vertical. Tiene
interpretación práctica solo cuando el cero está en el rango de
X.
2 β1 = β1 =
representa la pendiente de la recta, o sea la variación en Y por
unidad de cambio en X.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

59. Undécima sección
Estimación de los parámetros de la regresión
Denición
3 σ2 = MCE =
Una varianza mayor que cero quiere decir que en la práctica no
existe una relación perfecta entre Y y X: se obtienen valores
de Y que uctúan alrededor de una recta. Esta uctuación
está descrita por los errores εi cuya varianza se estima con la
MCE.
4 µy.j = y
La igualdad implica que la ecuación de regresión puede usarse
como una ecuación de predicción de valores medios de Y .
Para un valor de la concentración X dentro de su rango de
validez, se puede estimar el valor promedio de la DO mediante
y. Así, para X = 310, la DO promedio será y = 0.34. El
pronóstico es válido para valores de X en el rango elegido u
obtenido en el muestreo.[1]
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

60. Undécima sección
Estimación de los parámetros de la regresión
Empleando intervalos de conanza para la estimación de los
parámetros :
b ± tα/2,n−2Sb (12)
donde Sb = MCE/Sxx.
y ± tα/2,n−2S (yj) (13)
donde S2 (yj) = MCE
1
n
+
(xj − ¯x)2
Sxx
.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

61. Undécima sección
Estimación de los parámetros de la regresión
Empleando intervalos de conanza para la estimación de los
parámetros :
b ± tα/2,n−2Sb (12)
donde Sb = MCE/Sxx.
y ± tα/2,n−2S (yj) (13)
donde S2 (yj) = MCE
1
n
+
(xj − ¯x)2
Sxx
.
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple

62. Undécima sección
Bibliográa
Díaz, A., Diseño estadístico de experimentos, Universidad de
Antioquia, 2a edición, Medellin, 2009
Gutiérrez, H. and De la Vara, R., Análisis y diseño de
experimentos. Mc Graw Hill, 3a edición Mexico, D.F., 2012.
Montgomery, D. Diseño y análisis de experimentos.
Iberoamérica S.A., Mexico, D.F., 1991.
Kuehl, R.O. and Osuna, M.G. Diseño de experimentos:
principios estadísticos de diseño y análisis de investigación.2a.
Ed., Thomson Learning. Mexico, 2001.
Samuels, M.L. and Witmer, J.A. and Schaner, A.A.,
Fundamentos de estadística para las ciencias de la vida,
Pearson, 4a edición, Madrid. 2012
MSc. Edgar Madrid Cuello. Dpto de Matemática, UNISUCRE Análisis y diseño de experimentosRegresión lineal simple