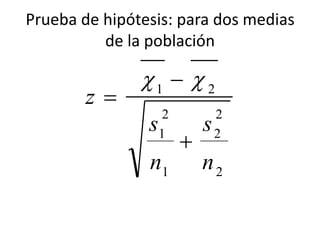
Este documento describe el proceso de prueba de hipótesis, incluyendo: 1) plantear una hipótesis nula y una hipótesis alternativa, 2) seleccionar un nivel de significancia, 3) calcular un estadístico de prueba, 4) formular una regla de decisión, y 5) tomar una decisión de rechazar o no rechazar la hipótesis nula. Proporciona ejemplos de cómo probar si la edad promedio de los aviones comerciales en los EE. UU. es de 15 años usando una p

1. Prueba de hipótesis

2. Hipótesis
• Suposición.
• Vínculo entre la teoría y la investigación.
• Parámetro de la población.

3. Prueba de hipótesis
• Se basa en evidencia y teoría de la
probabilidad para determinar si la hipótesis es
razonable.

4. ¿Cómo comprobar una hipótesis?
1. Plantear la hipótesis nula y la hipótesis
alternativa.
2. Seleccionar un nivel de significancia.
3. Calcular el estadístico de prueba.
4. Formular la regla de decisión.
5. Tomar una decisión.

5. Hipótesis nula e hipótesis alternativa
• La edad media de los aviones comerciales en
EEUU es de 15 años.
H0 µ=15
(Siempre es =,
porque es la declaración a prueba).
Hi µ≠15
(Sólo se observa si se demuestra que no es
verdadera la nula).

6. Nivel de significancia
α
Valor = Cualquiera entre 0 y 1.
.1 para encuestas políticas.
.05 en productos de artículos de consumo.
.01 en aseguramiento de calidad.

7. Estadístico de prueba
z
t-Student
F
X2 Ji cuadrada

8. Regla de decisión
• Valor crítico. Punto de
división entre la región
que se rechaza la
hipótesis nula y la
región que no se
rechaza.

9. Distribución Z como estadístico de
prueba (desviación estándar de la
población conocida)
n
z
/
 


10. Ejercicios

11. Pruebas de significancia de una y dos
colas
• La prueba es de una cola si H1 µ > ó µ <.
• Ejercicios.
• La prueba es de dos colas si H1 no establece
dirección.
• Ejercicios.

12. Valor p
• La probabilidad de observar un valor de
prueba tan extremo como, o más personal
que, el valor observado, dado que la hipótesis
nula es verdadera.

13. • Este proceso compara la probabilidad,
llamado valor p, con el nivel de significancia.
• Si el valor p es menor que el nivel de
significancia, se rechaza H0; si es mayor que el
nivel de significancia, H0 no se chaza.

14. Interpretación del peso de la evidencia
contra H0
• Si el valor de p es menor que:
– 0.10, se tiene alguna evidencia de que H0 no es
verdadera.
– 0.05, se tiene una firme evidencia de que H0 no es
verdadera.
– 0.01, se tiene una evidencia muy firme de que H0
no es verdadera.
– 0.001, se tiene una evidencia extremadamente
firme de que H0 no es verdadera.

15. Prueba de la media de la población:
muestra grande y desviación estándar
de la población desconocida
ns
z
/
 

En tanto el tamaño de la muestra (n) sea mayor que 30,

16. Ejercicios

17. Prueba de hipótesis: para dos medias
de la población
2
2
2
1
2
1
21
n
s
n
s
z





18. Ejercicios