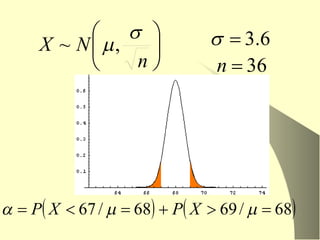
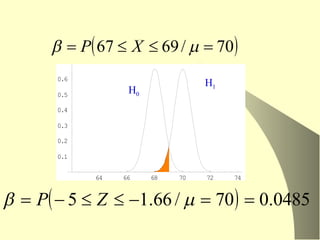
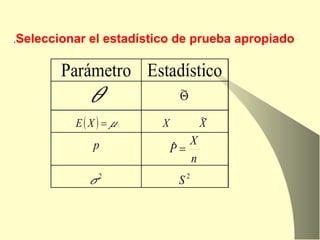
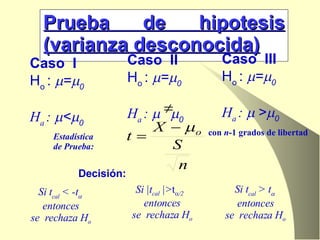
El documento trata sobre inferencia estadística y pruebas de hipótesis. Explica los conceptos clave como hipótesis nula y alternativa, errores tipo I y II, y el procedimiento general para realizar pruebas de hipótesis, incluyendo la selección del estadístico de prueba y la región crítica. También cubre pruebas específicas para medias, proporciones, comparaciones entre dos medias y medias pareadas.

1. INFERENCIA ESTADÍSTICA La Inferencia Estadística comprende los métodos que son usados para obtener conclusiones acerca de la población en base a una muestra tomada de ella. Incluye los métodos de estimación de parámetros y las pruebas de hipótesis. M P obtención de la muestra conclusiones

2. Inferencia para Proporciones es la proporción muestral. p representa la proporción poblacional que se desea estimar Cuando estamos interesados en estimar la proporción p (o el porcentaje) de ocurrencia de un evento. Se necesita definir una variable aleatoria X que indique el número de veces que ocurre el evento en una muestra de tamaño n y con probabilidad de éxito, p . Se puede mostrar que cuando el tamaño de muestra es grande, tal que np > 5, entonces el estadístico

3. Intervalo de confianza para la Proporción Intervalo de confianza ( aproximado) del 100 (1-  ) % para la proporción poblacional p es:

4. Problema de test de hipótesis: Una empresa constructora acaba de comprar una gran cantidad de cables con garantía de resistencia promedio de al menos de 7000 psi. Con la finalidad de verificar esto, ha decidido tomar una muestra de 10 cables para verificar su resistencia. Después usará los resultados del experimento para decidir si acepta o no la hipótesis del fabricante de cables, de que la media poblacional es por lo menos de 7000 libras por pulgadas cuadradas.

5. Problema de test de hipótesis Se busca comprobar alguna información o afirmación (conjetura) sobre la población a partir de los datos obtenidos de una muestra. Menos del 3% de las bombillas de un lote de 5000 duran menos de 1000 horas. Las bombillas duran más de 1000 horas en promedio. La resistencia media poblacional es por lo menos de 7000 psi.

6. Es una aseveración o conjetura con respecto a una o más poblaciones. Es una afirmación que se hace acerca de un parámetro o varios parámetros poblacional. La verdad o falsedad de una hipótesis estadística nunca llega a ser conocida con certeza. No se considera la población, sino una muestra aleatoria. Hipótesis Estadística

7. Test de hipótesis Se busca evidencia en los datos de la muestra para apoyar la hipótesis o para rechazar la hipótesis. La aceptación o no rechazo de una hipótesis implica que los datos no dan suficiente evidencia para rechazarla. El rechazo implica que la evidencia muestral es suficiente para rechazarla.

8. Hipótesis Nula y Alternativa H 0 : Cualquier aseveración que deseamos probar. H 1 : Hipótesis alternativa. Se espera que sea rechazada después de aplicar una prueba estadística La afirmación que se espera sea aceptada después de aplicar una prueba estadística.

9. Hipótesis Nula y Alternativa La resistencia media poblacional es por lo menos de 7000 libras por pulgadas cuadradas. La resistencia media poblacional es menos de 7000 libras por pulgadas cuadradas.

10. Tipos de Errores

11. Tipos de Errores Error de tipo II : Aceptar la hipótesis nula cuando ésta en la realidad es Falsa. Error de tipo I: Rechazar la hipótesis nula cuando ésta en la realidad es verdadera.

12. Nivel de significancia Probabilidad del error tipo II Una disminución de provoca un crecimiento en

13. 1-  se le llama la potencia de la prueba. Potencia de la prueba Una buena prueba estadística es aquella que tiene una potencia de prueba alta.

14. ¿Mejor balance entre los errores tipo I y tipo II? Regla general Nivel de error tipo II = 4 veces Nivel de error tipo I Si el nivel de error tipo I = 5% un adecuado nivel de error tipo II es 20% (potencia = 80%)

15. H o :  = 68 Ejemplo Una media muestral que cae cercana a 68 se consideraría como evidencia a favor de H 0 Una media muestral considerablemente menor o mayor que 68 se consideraría como evidencia a favor de H 1

16. Estadístico de prueba: Región crítica: Región de aceptación o no rechazo de H 0 : 67 68 69 Aceptar H 0 Rechazar H 0 Rechazar H 0

18. 9.5% de todas las muestras de tamaño 36 nos llevarán a rechazar que la media es 68. El nivel de significancia puede reducirse ampliando la región de aceptación o aumentando el tamaño de la muestra. La reducción del nivel de significancia no es suficiente para garantizar un buen procedimiento de prueba. Debemos ver el error tipo II.

19. H 1 H 0

20. Procedimiento de test Hipótesis Establecer la H 0 Elegir una hipótesis alternativa adecuada. Elegir un nivel de significancia  . Seleccionar el estadístico de prueba apropiada y establecer la región crítica. Calcular el valor del estadístico de prueba a partir de la muestra. Rechazar H 0 si la estadística de prueba tiene un valor en la región crítica.

21. Establecer la H 0 Elegir una hipótesis alternativa adecuada. Elegir un nivel de significancia  . . Seleccionar el estadístico de prueba apropiada y establecer la región crítica. Calcular el valor del estadístico de prueba a partir de la muestra. Rechazar H 0 si la estadística de prueba tiene un valor en la región crítica. Procedimiento de test Hipótesis

22. De una población normal con media desconocida  y varianza conocida  2 Prueba de Hipótesis relacionadas con la media de una Población Normal Varianza conocida Se desea probar la hipótesis:

23. Establecer la H 0 Elegir una hipótesis alternativa adecuada. Elegir un nivel de significancia  . . Seleccionar el estadístico de prueba apropiada y establecer la región crítica. Calcular el valor del estadístico de prueba a partir de la muestra. Rechazar H 0 si la estadística de prueba tiene un valor en la región crítica. Procedimiento de test Hipótesis

24. Contra la alternativa: Elegir una hipótesis alternativa adecuada

25. Establecer la H 0 Elegir una hipótesis alternativa adecuada. Elegir un nivel de significancia  . . Seleccionar el estadístico de prueba apropiada y establecer la región crítica. Calcular el valor del estadístico de prueba a partir de la muestra. Rechazar H 0 si la estadística de prueba tiene un valor en la región crítica. Procedimiento de test Hipótesis

26. Establecer la H 0 Elegir una hipótesis alternativa adecuada. Elegir un nivel de significancia  . . Seleccionar el estadístico de prueba apropiado y establecer la región crítica. Calcular el valor del estadístico de prueba a partir de la muestra. Rechazar H 0 si la estadística de prueba tiene un valor en la región crítica. Procedimiento de test Hipótesis

27. . Seleccionar el estadístico de prueba apropiado

28. Se distribuye como una normal estándar. Una muestra aleatoria de tamaño n . |Z |> Z  /2 La Región crítica:

29. Establecer la H 0 Elegir una hipótesis alternativa adecuada. Elegir un nivel de significancia  . . Seleccionar el estadístico de prueba apropiada y establecer la región crítica. Calcular el valor del estadístico de prueba a partir de la muestra. Rechazar H 0 si la estadística de prueba tiene un valor en la región crítica. Procedimiento de test Hipótesis

30. Calcular el valor del estadístico de prueba a partir de la muestra.

31. Establecer la H 0 Elegir una hipótesis alternativa adecuada. Elegir un nivel de significancia  . . Seleccionar el estadístico de prueba apropiada y establecer la región crítica. Calcular el valor del estadístico de prueba a partir de la muestra. Rechazar H 0 si la estadística de prueba tiene un valor en la región crítica. Procedimiento de test Hipótesis

32. Rechazar H 0 si la estadística de prueba tiene un valor en la región crítica. Si |z cal |> Z  /2 entonces se rechaza H o

33. Fórmulas para prueba de hipotesis de medias Caso I H o :  =  0 H a :  <  0 Estadística de Prueba: Caso III H o :  =  0 H a :  >  0 Si Z cal < -Z  entonces se rechaza H o Decisión: Si |Z cal |> Z  /2 entonces se rechaza H o Si Z cal > Z  entonces se rechaza H o Caso II H o :  =  0 H a :   0

34. Prueba de hipotesis usando “p-values” El “P-value” llamado el nivel de significación observado, es el valor de  al cual se rechazaría la hipótesis nula si se usa el valor calculado de la prueba estadística. Un “P-value” cercano a 0 indica un rechazo de la hipótesis nula. Así un “P-value” menor que .05 indicará que se rechaza la hipótesis nula.

35. Prueba de hipotesis usando “p-values” Fórmulas para calcular “P-value”: Si Ha:  >  o , entonces P-value = P ( Z>Zcalc ). Si Ha:  <  o , entonces P-value = P ( Z<Zcalc ). Si Ha:   o , entonces P-value = 2P ( Z >| Zcalc | ).

36. Prueba de hipotesis (varianza desconocida) Caso I H o :  =  0 H a :  <  0 Estadística de Prueba: Caso III H o :  =  0 H a :  >  0 Decisión: Si t cal < -t  entonces se rechaza H o Si |t cal |> t  /2 entonces se rechaza H o Si t cal > t  entonces se rechaza H o con n -1 grados de libertad Caso II H o :  =  0 H a :   0

37. Comparación entre dos medias poblacionales usando muestras independientes Supongamos que se tienen dos poblaciones distribuidas normalmente con medias desconocidas  1 y  2 , respectivamente. Se puede aplicar una prueba t de Student para comparar las medias de dichas poblaciones basándonos en dos muestras independientes tomadas de ellas. Si las varianzas de las poblaciones son iguales pero desconocidas

38. La varianza poblacional es estimada por una varianza combinada de las varianzas de las dos muestras tomadas. Un intervalo de confianza del 100(1-  ) % para la diferencia  1 -  2 de las medias poblacionales será de la forma:

39. Las pruebas de hipótesis son: Caso I Caso II Caso III Ho : Ho : Ho : Ha : Ha : Ha : Prueba Estadística: Decisión: Si < Si < o > Si > se rechaza Ho se rechaza Ho se rechaza Ho con m + n -2 grados de libertad

40. Si las varianzas de las poblaciones no son iguales , entonces se usa una prueba aproximada de t , donde el número de grados de libertad es calculado aproximadamente. La prueba de t aproximada está dada por: donde los grados de libertad gl son aproximados por la siguiente fórmula:

41. Comparando media de dos poblaciones usando muestras pareadas En este caso se trata de comparar dos métodos o tratamientos, pero se quiere que las unidades experimentales donde se aplican los tratamientos sean las mismas, ó lo más parecidas posibles, para evitar influencia de otros factores en la comparación

42. Las inferencias que se hacen son acerca del promedio poblacional  d de las d i . Si  d = 0, entonces significa que no hay diferencia entre los dos tratamientos. Consideremos d i = X i - Y i la diferencia de los tratamientos en el i-ésimo sujeto. Sea X i el valor del tratamiento I y Y i el valor del tratamiento II en el i-ésimo sujeto.

43. Pruebas de Hipótesis Caso I Caso II Caso III Ho :  d = 0 Ho :  d = 0 Ho :  d =0 Ha :  d < 0 Ha :  d  0 Ha :  d >0 Prueba Estadística: Decisión: Si tcalc<- t  Si | tcal |> t  /2 Si tcal > t  Se rechaza H 0

44. Test de hipótesis para Proporciones Prueba Estadística (Aproximada): Decisión S i Zcal <-Z  S i | Zcal |> Z  / 2 S i Zcal >Z  entonces entonces entonces se rechaza H o se rechaza H o se rechaza H o Caso I Caso II Caso III H o : p=p 0 H o : p=p 0 H o : p=p 0 H a : p<p 0 H a : p p 0 H a : p>p 0