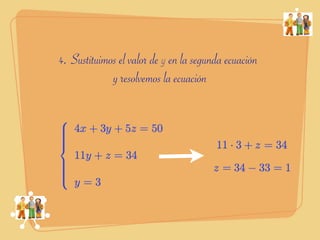
El documento describe un problema de sistemas de ecuaciones lineales para determinar las edades de tres hermanos. Se plantean tres ecuaciones igualadas a 50, 46 y 60 respectivamente en función de las edades x, y y z. Se aplica el método de Gauss para resolver el sistema, eliminando sucesivamente las incógnitas y resolviendo cada ecuación hasta obtener las edades: x=9 años, y=3 años, z=1 año.

1. Problemas de sistemas de
ecuaciones lineales
Método de Gauss

2. Las edades de tres hermanos son tales que el cuádruplo de la edad
del primero más el triple de la edad del segundo, más el quíntuplo de
la del tercero, es igual a 50. El triple de la edad del primero, más el
quíntuplo de la del segundo, más el cuádruplo de la del tercero, es
igual a 46. Y el quíntuplo de la edad del primero, más el cuádruplo
de la edad del segundo, más el triple de la edad del tercero, es igual
a 60.
(a) Plantea un sistema de ecuaciones que permita determinar las
edades de los tres hermanos
(b) Resolver el sistema de ecuaciones aplicando el método de Gauss

3. Planteamos el problema, para ello designamos por:
x es la edad del hermano mayor
y es la edad del hermano mediano
z es la edad del hermano menor
Y las ecuaciones vienen dadas por:

4. Para resolver aplicamos el método de Gauss:
Consiste en construir un sistema de ecuaciones equivalente
a este, donde la primera ecuación aparezcan las tres
incógnitas, en la segunda dos incógnitas y en la tercera
sólo una, es decir, un sistema escalonado.
Una vez conseguido esto, resolvemos la tercera ecuación,
obteniendo una de las incógnitas, la solución la sustituimos
en la segunda ecuación y obtenemos la segunda incógnita,
y sustituimos en la primera con lo que obtenemos la última
de las incógnitas

5. 1. Tratamos en este paso de eliminar una de las
incógnitas en la segunda y tercera ecuación, por
ejemplo la x
2ª=4·2ª-3·1ª
3ª=5·2ª-3·3ª

6. 2.Eliminamos de la tercera ecuación una de las dos
incógnitas, por ejemplo la z
3ª=11·2ª-3ª

7. 3. Resolvemos la tercera ecuación

8. 4. Sustituimos el valor de y en la segunda ecuación
y resolvemos la ecuación

9. 4. Sustituimos el valor de y y z en la primera
ecuación y resolvemos la ecuación

10. Por tanto tenemos que las edades de los niños son:
El primero tiene 9 años
El segundo tiene 3 años
El tercero tiene 1 año