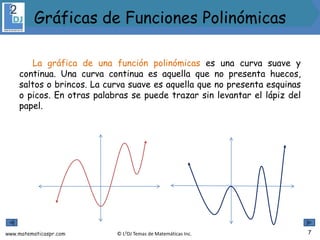
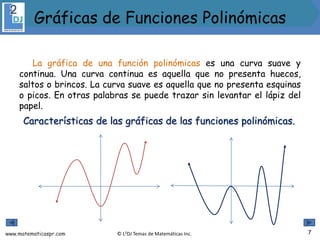
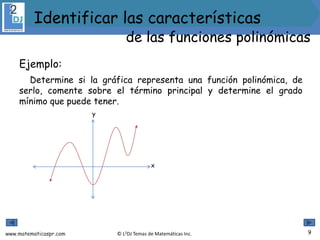
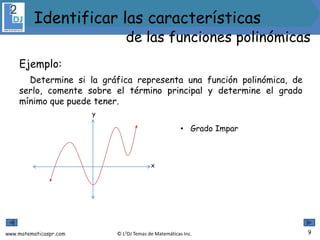
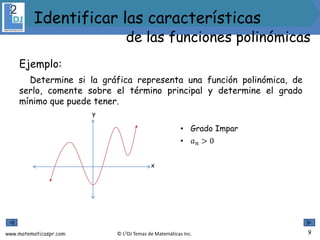
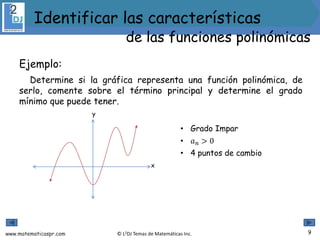
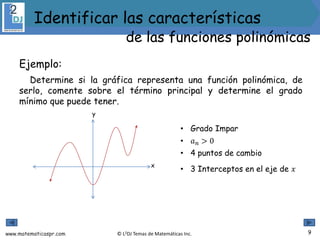
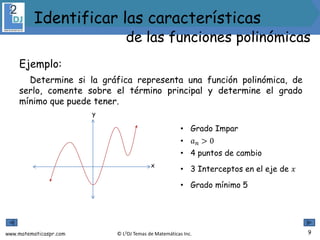
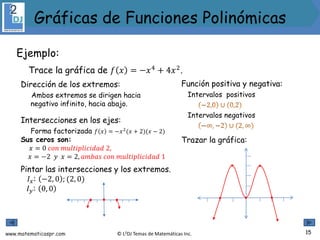
El documento aborda las funciones polinómicas, describiendo su definición, características y métodos para identificar su grado, ceros y gráficas. Se explican teoremas relevantes, como el de los ceros racionales y el teorema de la raíz conjugada, así como la forma factorizada de estas funciones. Además, se presentan ejemplos y ejercicios para aplicar los conceptos aprendidos.