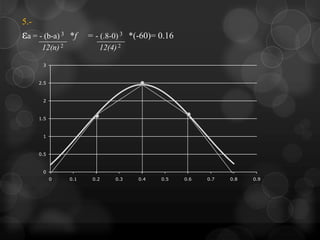
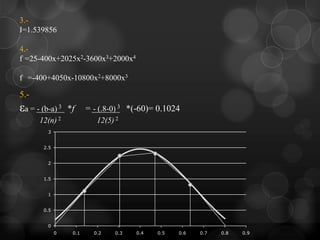
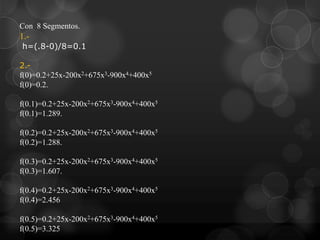
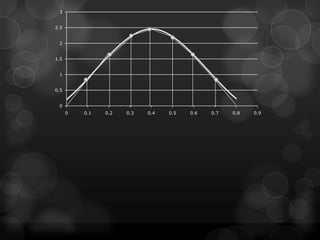
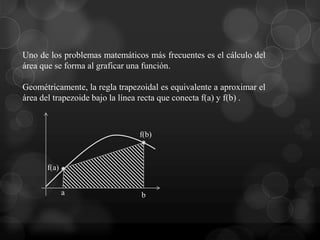
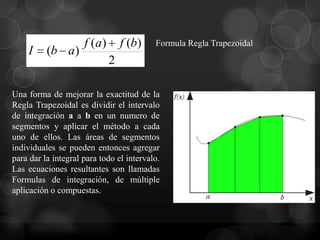
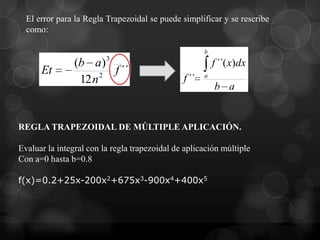
Este documento presenta la regla del trapecio, un método numérico para calcular el área bajo una curva dividiendo el intervalo en subáreas trapezoidales. Explica cómo aplicar la regla del trapecio simple y múltiple para aproximar la integral de diferentes funciones, y cómo el error se reduce al aumentar el número de subdivisiones.

1. INSTITUTO TECNOLOGICO DE CIUDAD VALLES
REGLA DEL TRAPECIO
DE APLICACIÓN MULTIPLE
METODOS NUMERICOS
ING. OMAR MURRIETA POZOS
FECHA: 19 DE ABRIL DE 2012 CIUDAD VALLES

2. EQUIPO #1
INTEGRANTES:
 BUSTAMANTE TREJO ROBERTO ZENAIDO
 CASTRO RODRIGUEZ EDUARDO
 FLORES FERNANDEZ CARLOS ALBERTO
 GONZALEZ RIVERA JORGE ALBERTO
 MONTES SANCHEZ DIEGO
 TORRES HERNANDEZ ROSA MARIA

3. INTRODUCCION
La regla trapezoidal es la primera de las formulas de integración
cerrada de Newton-Cotes.
Las formulas de integración de Newton-Cotes son los esquemas de
integración numérica mas comunes. Se basan en la estrategia de
remplazar una función complicada o datos tabulados con una
función aproximada que sea fácil de integrar.
OBJETIVO
Resolver el problema de cálculo del área bajo la curva entre dos
límites conocidos, dividiendo en N sub áreas para calcular su valor
asumiendo cada sub área como un pequeño trapecio.

4. Uno de los problemas matemáticos más frecuentes es el cálculo del
área que se forma al graficar una función.
Geométricamente, la regla trapezoidal es equivalente a aproximar el
área del trapezoide bajo la línea recta que conecta f(a) y f(b) .
f(b)
f(a)
a b

5. f (a) f (b) Formula Regla Trapezoidal
I (b a)
2
Una forma de mejorar la exactitud de la
Regla Trapezoidal es dividir el intervalo
de integración a a b en un numero de
segmentos y aplicar el método a cada
uno de ellos. Las áreas de segmentos
individuales se pueden entonces agregar
para dar la integral para todo el intervalo.
Las ecuaciones resultantes son llamadas
Formulas de integración, de múltiple
aplicación o compuestas.

6. Formato General de la Ecuación Trapezoidal Múltiple
n 1
f ( x0 ) 2 f ( xi ) f ( xn )
i 1
I (b a)
2n
Un error para la Regla Trapezoidal de múltiple aplicación se puede
obtener al sumar los errores individuales de cada segmento para dar.
(b a ) 3 n
Et f ´´( i )
12 n 3 i 1

7. El error para la Regla Trapezoidal se puede simplificar y se rescribe
como:
b
(b a)3 f ´´( x)dx
Et 2
f ´´ a
12 n f ´´
b a
REGLA TRAPEZOIDAL DE MÚLTIPLE APLICACIÓN.
Evaluar la integral con la regla trapezoidal de aplicación múltiple
Con a=0 hasta b=0.8
f(x)=0.2+25x-200x2+675x3-900x4+400x5

8. 3
2.5
2
1.5
1
0.5
0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
Solución:
Con dos segmentos.
1.- Calcular los segmentos individuales.
h=(b-a)/n n= Numero de segmentos
h=(.8-0)/2=0.4

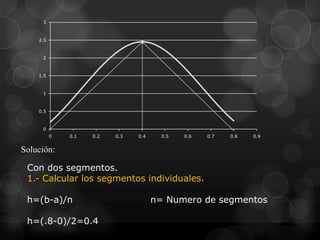
9. 2.- Hacer la sustitución de los segmentos en la función.
f(0)=0.2+25x-200x2+675x3-900x4+400x5
f(0)=0.2.
f(0.4)=0.2+25x-200x2+675x3-900x4+400x5
f(0.4)=2.456
f(0.8)=0.2+25x-200x2+675x3-900x4+400x5
f(0.8)=.232
3.- Aplicar la Formula General de la Regla Trapezoidal.
n 1
f ( x0 ) 2 f ( xi ) f ( xn )
i 1
I (b a)
2n
I=(.8-0)[0.2+2(2.456)+.232]
2(2)
I=1.0688

10. 0.8
0

11. 5.- Calcular el error.
εa = - (b-a) 3 *f = - (.8-0) 3 *(-60)= 0.64
12(n) 2 12(2) 2
En el caso que se deseen calcular con mas segmentos se sigue la misma
Metodología anterior.
Con 4 Segmentos.
1.-
h=(.8-0)/4=0.2
2.-
f(0)=0.2+25x-200x2+675x3-900x4+400x5
f(0)=0.2.
f(0.2)=0.2+25x-200x2+675x3-900x4+400x5
f(0.2)=1.28

12. f(0.4)=0.2+25x-200x2+675x3-900x4+400x5
f(0.4)=2.456
f(0.6)=0.2+25x-200x2+675x3-900x4+400x5
f(0.6)=3.464
f(0.8)=0.2+25x-200x2+675x3-900x4+400x5
f(0.8)=0.232
3.-
I=1.4848
4.-
f =25-400x+2025x2-3600x3+2000x4
f =-400+4050x-10800x2+8000x3

13. 5.-
εa = - (b-a) 3 *f = - (.8-0) 3 *(-60)= 0.16
12(n) 2 12(4) 2
3
2.5
2
1.5
1
0.5
0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

14. Con 5 Segmentos.
1.-
h=(.8-0)/5=0.16
2.-
f(0)=0.2+25x-200x2+675x3-900x4+400x5
f(0)=0.2.
f(0.16)=0.2+25x-200x2+675x3-900x4+400x5
f(0.16)=1.2969.
f(0.32)=0.2+25x-200x2+675x3-900x4+400x5
f(0.32)=1.7433
f(0.48)=0.2+25x-200x2+675x3-900x4+400x5
f(0.48)=3.1860
f(0.64)=0.2+25x-200x2+675x3-900x4+400x5
f(0.64)=3.1890
f(0.8)=0.2+25x-200x2+675x3-900x4+400x5
f(0.8)=.232

15. 3.-
I=1.539856
4.-
f =25-400x+2025x2-3600x3+2000x4
f =-400+4050x-10800x2+8000x3
5.-
εa = - (b-a) 3 *f = - (.8-0) 3 *(-60)= 0.1024
12(n) 2 12(5) 2
3
2.5
2
1.5
1
0.5
0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

16. Con 8 Segmentos.
1.-
h=(.8-0)/8=0.1
2.-
f(0)=0.2+25x-200x2+675x3-900x4+400x5
f(0)=0.2.
f(0.1)=0.2+25x-200x2+675x3-900x4+400x5
f(0.1)=1.289.
f(0.2)=0.2+25x-200x2+675x3-900x4+400x5
f(0.2)=1.288.
f(0.3)=0.2+25x-200x2+675x3-900x4+400x5
f(0.3)=1.607.
f(0.4)=0.2+25x-200x2+675x3-900x4+400x5
f(0.4)=2.456
f(0.5)=0.2+25x-200x2+675x3-900x4+400x5
f(0.5)=3.325

17. 2.-
f(0.6)=0.2+25x-200x2+675x3-900x4+400x5
f(0.6)=3.464
f(0.7)=0.2+25x-200x2+675x3-900x4+400x5
f(0.7)=2.363
f(0.8)=0.2+25x-200x2+675x3-900x4+400x5
f(0.8)=0.232
3.-
I=1.6008
4.-
f =25-400x+2025x2-3600x3+2000x4
f =-400+4050x-10800x2+8000x3
5.-
εa = - (b-a) 3 *f = - (.8-0) 3 *(-60)= 0.0399
12(n) 2 12(8) 2

18. 3
2.5
2
1.5
1
0.5
0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9