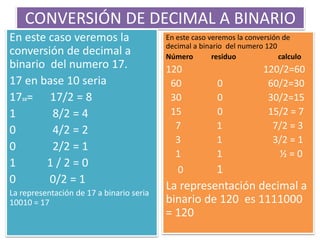
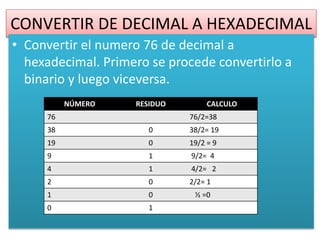
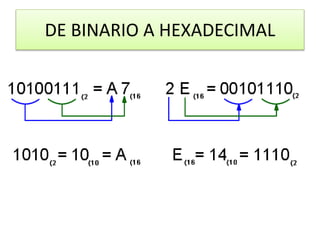
Este documento presenta información sobre las conversiones entre los sistemas binario, decimal, hexadecimal y octal. Explica cómo convertir números entre estas bases a través de ejemplos como convertir 16 decimal a binario (10000), 17 binario a decimal (10010 = 17), y 76 decimal a hexadecimal (4C). También cubre la conversión de binario a hexadecimal, decimal a octal, y métodos adicionales para las diferentes conversiones entre bases numéricas.

1. UNIVERSIDAD TECNOLÓGICA DE PANAMÁ
CAMINO A LA EXCELENCIA A TRAVÉS DEL MEJORAMIENTO CONTINUO
ASIGNATURA: TECNOLOGÍA INFORMÁTICA.
ASIGNACION Nº 2 SISTEMA BINARIO
ELABORADO POR: JOSÉ DE LA CRUZ FLORES
CED. 4-204-830
A CONSIDERACIÓN DEL: PROFESOR MARTIN AROSEMENA
FECHA DE ENTREGA
18/7/2014

2. INTRODUCCION
Al empezar este trabajo y la culminación valió la
pena investigar mas sobre temas que no son
desconocidos pero que a lo largo de camino se
pierden pero he retomado nuevamente los
conocimientos previos para poder desarrollar
este trabajo.

3. CONVERSIÓN DE BINARIO A DECIMAL
Convertir el numero 16 de binario a decimal
Numero residuo calculo
16 16/2=8
8 0 8/2=4
4 0 4/2=2
2 0 2/2=1
1 0 ½ =0
0 1
La conversión de 16 seria 10000 =16

4. CONVERSIÓN DE DECIMAL A BINARIO
En este caso veremos la
conversión de decimal a
binario del numero 17.
17 en base 10 seria
1710= 17/2 = 8
1 8/2 = 4
0 4/2 = 2
0 2/2 = 1
1 1 / 2 = 0
0 0/2 = 1
La representación de 17 a binario seria
10010 = 17
En este caso veremos la conversión de
decimal a binario del numero 120
Número residuo calculo
120 120/2=60
60 0 60/2=30
30 0 30/2=15
15 0 15/2 = 7
7 1 7/2 = 3
3 1 3/2 = 1
1 1 ½ = 0
0 1
La representación decimal a
binario de 120 es 1111000
= 120

5. CONVERTIR DE DECIMAL A HEXADECIMAL
• Convertir el numero 76 de decimal a
hexadecimal. Primero se procede convertirlo a
binario y luego viceversa.
NÚMERO RESIDUO CALCULO
76 76/2=38
38 0 38/2= 19
19 0 19/2 = 9
9 1 9/2= 4
4 1 4/2= 2
2 0 2/2= 1
1 0 ½ =0
0 1

6. CONVERSIÓN DE BINARIO A DECIMAL
• Para convertir un número binario a un número
decimal, basta con aplicar la fórmula general
presentada para la representación de números en un
sistema posicional, pero en este caso, teniendo en
cuenta que la base es 2.
• Como ejemplo vamos a ver cómo transformamos el
número binario de seis dígitos 110101 a decimal:
• 110101 = 1 × 25 + 1 × 24 + 0 × 23 + 1 × 22 + 0 × 21 + 1 × 20 =
• = 1 × 32 + 1 × 16 + 0 × 8 + 1 × 4 + 0 × 2 + 1 × 1 =
• = 32 + 16 + 4 + 1 = 53

7. CONVERTIR DE DECIMAL A
HEXADECIMAL
Aquí se podrá convertir numero 41053 decimal
a hexadecimal.
41053 41053/16=2565.8125
2565 08125/16=13
160 2565/16= 160.3125
10 03125/16=5
160/16= 10
00x16= 0
10ª
A 0 5 D = 41053

8. CONVERSIÓN DE DECIMAL A OCTAL
Convertir Numero binario 1001100
a hexadecimal =
1100 = 0x2^0+1x2^1+0x2^2 =0x1+1x2+1x4=0+2+4=6
010
0x2^0+1x2^1+0x2^2=ox1+1x2+0x4=0x2+0=2
62 seria representa el octal del número 110010 binario que a su
ves era representación en base 2 del número decimal 50
Decimal=50
Binario = 110010
Octal = 62

9. CONVERTIR DE DECIMAL A OCTAL MAS
SENCILLO
• Calcular y convertir el numero 150 de decimal
a octal.
150 8
6 18
2 8
2 = 226(8)

10. CONVERTIR DE BINARIO A
HEXADECIMAL
convertir 128 de binario a hexadecimal
1000 1100
8 8+4 =12
8 8C
El 128 representa el 8c hexadecimal
128 64 32 16 8 4 2 0
1 0 0 0 1 1 0 0

11. DE BINARIO A HEXADECIMAL

12. EJEMPLOS ADICIONALES DE CADA
UNO DE LAS CONVERSIONES
• Ejemplo:
• Convertir los siguientes números decimales a formato
• binario:
• (a) 12 (b) 25 (c) 58 (d) 82
• Solución.
• (a) 12 = 8 + 4 = 23 + 22 ...................................................................1 1 0 0
• (b) 25 = 16 + 8 + 1 = 24 + 23 + 20 ……………………………1 1 0 0 1
• (c) 58 = 32 + 16 + 8 + 2 = 25 + 24 + 23 + 21 ………..1 1 1 0 1 0
• (d) 82 = 64 + 16 + 2 = 26 + 24 + 21 ……………………..1 0 1 0 0 1 0

13. DE BINARIO A DECIMAL
• Por ejemplo, 745 = 7 · 100 + 4 · 10 + 5 · 1
O lo que es lo mismo: 745 = 7 · 102 + 4 · 101 + 5 · 100
En el sistema binario, las cifras que componen el número
multiplican a las potencias de dos (1, 2, 4, 8, 16, ….)
20=1, 21=2, 22=4, 23=8, 24=16, 25=32, 26=64, ...
Por ejemplo, para pasar a binario un número decimal, empezamos
por la derecha y vamos multiplicando cada cifra por las sucesivas
potencias de 2, avanzando hacia la izquierda:
101102 = 0 · 1 + 1 · 2 + 1 · 4 + 0 · 8 + 1 · 16 = 2 + 4 + 16 = 2210
1102 = 0 · 1 + 1 · 2 + 1 · 4 = 2 + 4 = 610

14. De decimal a octal
• Paso 1: Dividir el número decimal 8 entonces el
cociente y el resto será 17 y 7 respectivamente
Paso 2: Dividir 17 por 8 entonces el cociente y el
resto será 2 y 1 respectivamente
Paso 3: El cociente 2 no puede ser dividido por 8
Paso 4: Para obtener el número resultante, anote
el último cociente primero y los restos de un nivel
inferior al nivel superior
El número Octal equivalente es (217)

15. Decimal a hexadecimal
16 317547
16
157
144
135
128
74
64
107
96
11
EJEMPLO
317547

16. DE BINARIO A
HEXADECIMAL

17. Al concluir este trabajo me fue de gran ayuda
para recordar los conocimientos adquiridos en la
carrera de licenciatura en informática. Pero ha
servido para reforzarlo y ahora ponerlos en
practica.