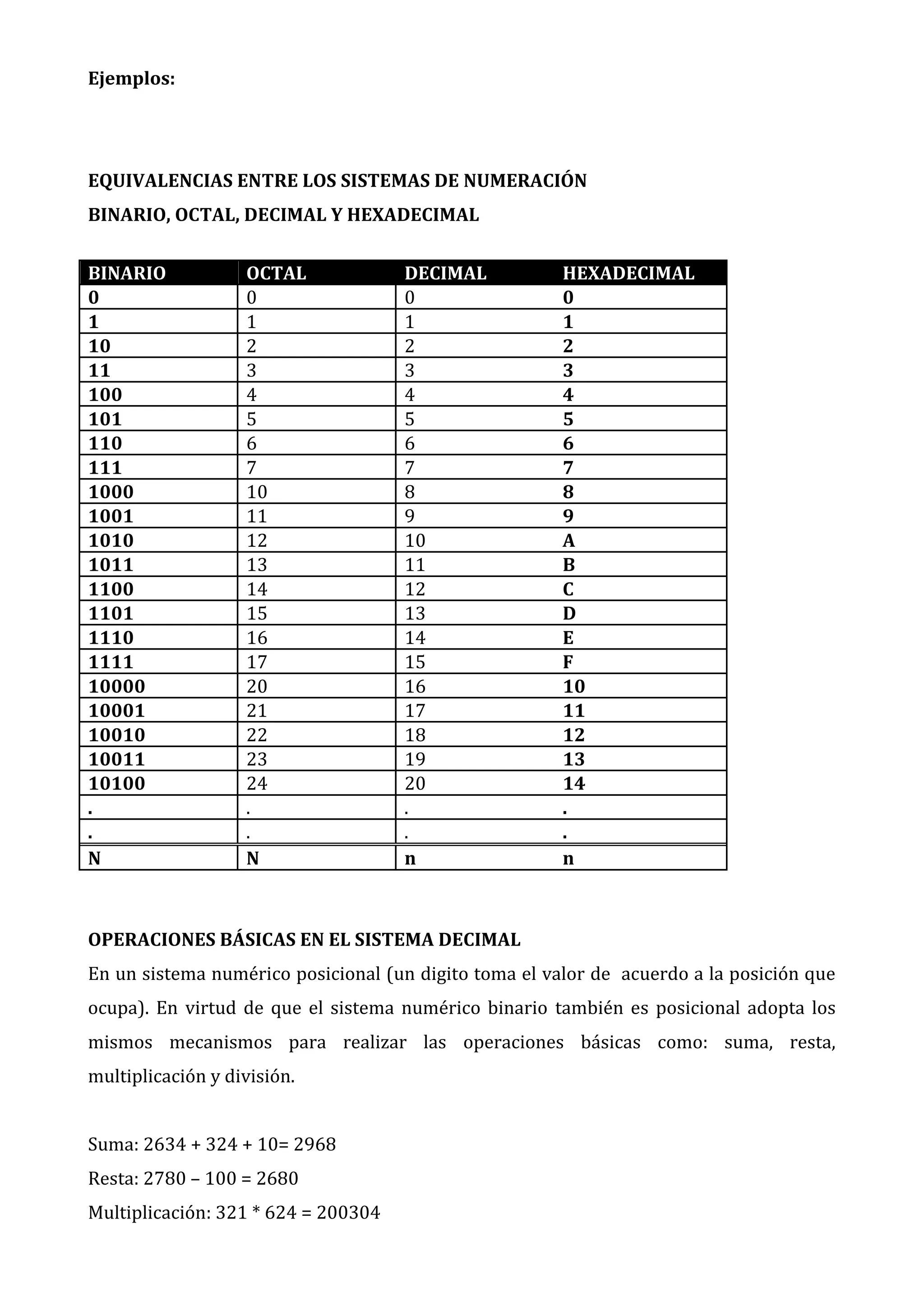
El documento describe diferentes sistemas de numeración como binario, octal, decimal y hexadecimal. Cada sistema tiene una base y conjuntos de dígitos distintos. Los sistemas de numeración son posicionales, donde el valor de cada dígito depende de su posición. También explica cómo convertir números entre estas bases usando divisiones sucesivas.

1. REPRESENTACIÓN INTERNA DE LOS DATOS
LOS SISTEMAS DE NUMERACIÓN: Es un conjunto de símbolos y reglas que se utiliza para
la representación de datos numéricos o cantidades.
Ejemplos:
Sistema de
Binario.
Sistema de
Octal.
Sistema de
Decimal.
Sistema de
Hexadecimal.
Sistema de
ASCII
Numeración
Base = 2
Dígitos: {0,1}
Numeración Base = 8
Dígitos: {0,1,2,3,4,5,6,7}
Numeración Base = 10
Dígitos: {0,1,2,3,4,5,6,7,8,9}
Numeración Base = 16
Dígitos:
{0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}
Dígitos: {x/x E Tabla ASCII}
Numeración Base = 256
Un sistema de numeración se caracteriza fundamentalmente por una base, que es el
número de símbolos distintos que utiliza, y además es el coeficiente que determina cual es
el valor de cada símbolo dependiendo de la posición que ocupe.
Los sistemas de numeración actual son posiciónales en los que el valor relativo que
representa cada símbolo o cifra de una determinada cantidad depende de su valor
absoluto y de posición relativa que ocupa dicha cifra con respecto a la coma decimal; el
valor que proporciona cada posición está íntimamente ligado al valor de la base del
sistema de numeración utilizado.
SISTEMAS NUMÉRICOS POSICIÓNALES
Un sistema numérico se dice que es posicional si el valor de cualquier digito toma un peso
de acuerdo a la posición que ocupa. Se utiliza el cero como indicador de cambio de
posición.
CONTEO DE LOS SISTEMAS NUMÉRICOS
El conteo de los sistemas numéricos se lo realiza de la siguiente manera:
1. Se escribe secuencialmente la n-dígito del sistema.
2. Una vez que se llega al último digito hay que volver a repetir la secuencia pero
acompañada de una unidad adicional en la columna continua.

2. Ejemplos:
EQUIVALENCIAS ENTRE LOS SISTEMAS DE NUMERACIÓN
BINARIO, OCTAL, DECIMAL Y HEXADECIMAL
BINARIO
0
1
10
11
100
101
110
111
1000
1001
1010
1011
1100
1101
1110
1111
10000
10001
10010
10011
10100
.
.
N
OCTAL
0
1
2
3
4
5
6
7
10
11
12
13
14
15
16
17
20
21
22
23
24
.
.
N
DECIMAL
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
.
.
n
HEXADECIMAL
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
10
11
12
13
14
.
.
n
OPERACIONES BÁSICAS EN EL SISTEMA DECIMAL
En un sistema numérico posicional (un digito toma el valor de acuerdo a la posición que
ocupa). En virtud de que el sistema numérico binario también es posicional adopta los
mismos mecanismos para realizar las operaciones básicas como: suma, resta,
multiplicación y división.
Suma: 2634 + 324 + 10= 2968
Resta: 2780 – 100 = 2680
Multiplicación: 321 * 624 = 200304

3. División: (Divisor)9/4(Dividendo) = 2 (cociente)
1(Resto)
SISTEMA BINARIO: Es un sistema numérico posicional de base 2 y como funciona cuyos
dígitos son 0 y 1.
Los dígitos del sistema binario también se lo conoce como bits es de gran trascendencia en
el área de computación debido a que los ordenadores trabajan con bits.
CONVERSIÓN DE NÚMEROS DE BASE 10 A BASE 2: Para convertir un numero decimal a
binario se lo hace mediante divisiones sucesivas para la base 2 y tomando los residuos de
abajo hacia arriba.
Ejemplos: Convertir 48 a binario.
4810 2
0
24
0
2
12
0
2
6
0
2
3
1
2
1
1
2
0
4810= 1100002
Convertir 86 a binario.
8610 2
0
43
1
8610= 10101102
2
21
1
2
10
0
2
5
1
2
2
0
2
1
1
2
0

4. Ejercicios propuestos:
1. 1034110
2. 54810
2. 24210
98710
3. 5369310
406910
4. 36710
9010
5. 1210
347810
CONVERSIÓN DE NÚMEROS DE BASE 2 A BASE 10
Para convertir un número binario utilizamos el siguiente procedimiento:
1. Colocamos los pesos de cada digito binario y comenzando desde la derecha con 2 a
la 0 potencia hasta asignarle el peso correspondiente al último bit de la izquierda.
2. Calculamos el valor de potencia de cada uno de los bits del número binario.
3. multiplicamos el valor de cada potencia por digito correspondiente del número
binario.
4. Sumar los pesos cuyo bit representativo sea 1.
Ejemplo:
Dado el siguiente numero binario 1001010102, convertirlo a decimal.
I
D
1
0
0
1
0
1
0
1
02
20
21
22
23
24
25
26
27
28
Ejercicios:
1. 1010102
101011012
2. 1011112
10101112
3. 101102
10100100010012
4. 10101012
1010101012
5. 10111102
1112
=
=
=
=
=
=
=
=
=
1
2
4
8
16
32
64
128
256
X
X
X
X
X
X
X
X
X
0
1
0
1
0
1
0
0
1
0
2
0
8
0
32
0
0
256
29810

5. CONVERSIÓN DE NÚMEROS DE BASE 10 A BASE 8
Se utiliza el método de divisiones sucesivas para la base 8: Consiste en dividir el número y
los sucesivos cocientes obtenidos por 8 hasta llegar a una división cuyo cociente sea 0. El
numero octal buscado es el compuesto por todos los retos obtenidos, escritos en orden
inverso a su obtención. Como puede observarse, este método es similar al método de
conversión de decimal a binario de las divisiones por 2.
Ejemplo: Convertir el numero decimal 500 a octal.
50010 8
4
62
6
8
7
7
8
0
50010= 7648.
Ejercicios:
1. 8382310
2. 39410
3. 450310
4. 484910
5. 937510
6. 842910
1. 19210
8. 623710
2. 73110
3. 23210
CONVERSIÓN DE NÚMEROS DE BASE 8 A BASE 10
Existen varios métodos, siendo el más generalizado el indicado por el TFN que hace la
conversión de forma directa por medio de la formula.
Ejemplos:
a) Convertir el número octal 7648 a decimal.
7
7 * 82
6
6 * 81
4
4 * 80
=
448 +
b) Convertir el número octal 7778 a decimal.
7
7
7
48 +
4
= 50010

6. 7 * 82
7 * 81
7 * 80
=
Ejercicios:
1. 75428
448 +
56 +
7
= 51110
3848
2. 27468
745218
3. 6537328
3648
4. 6418
54218
5. 79278
1238
CONVERSIÓN DE NÚMEROS DE BASE 10 A BASE 16
El método de divisiones sucesivas por 16: Se divide él número decimal y los cocientes
sucesivos por 16 hasta obtener un cociente igual a 0. Él numero hexadecimal buscado
será el compuesto por todos los restos obtenidos en orden inverso a su obtención.
Ejemplos:
1000
8
16
62
14
16
3
3
100010 = 3E816
Ejercicios:
1. 37110
9388310
2. 627310
721210
3. 9732310
282310
4. 18210
37410
5. 87210
6. 3410
16
0