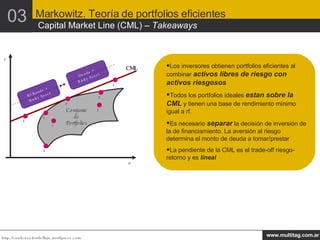
El documento resume conceptos clave sobre gestión de riesgos de inversión. En primer lugar, define los conceptos de riesgo, retorno esperado, desviación estándar y otras medidas de riesgo. Luego, introduce la Teoría de Portafolios de Markowitz sobre portafolios eficientes y la Frontera Eficiente. Finalmente, explica el Modelo de Valoración de Activos de Capital y la Línea del Mercado de Capitales.

1. Risk Management Universidad Católica Argentina Agosto 2007 Alejandro M. Salevsky Juan Manuel Cascone Pablo Techera Finanzas II

2. INVESTMENTS . Alex Kane and Alan Marcus Chapter 5: Risk and Risk Aversion, (page 142). Chapter 6: Capital Allocation between the Risky Asset and the Risk-free Asset, (page 170). Chapter 7: Optimal Risky Portfolios, (page 192). Chapter 8: The Capital Asset Pricing Model, (page 236). FUNDAMENTOS DE FINANZAS CORPORATIVAS . Richard Brealey & Stuart Myers Capítulo 7: Introducción al riesgo, retorno y el costo de oportunidad del capital. Captíulo 8: Riesgo y retorno. Bibliografía

3. 01 Conceptos Generales 02 Medición del riesgo en activos y portfolios. 03 Markowitz. Teoría de portfolios eficientes 04 Sensibilidad y Escenarios Índice

4. Concepto Está dado por la variabilidad de los retornos de un activo determinado Es la posibilidad que los flujos de fondos reales sean diferentes a los flujos de fondos pronosticados Si el retorno es conocido con certeza, es una inversión libre de riesgo Prima de riesgo La diferencia entre el retorno de un activo riesgoso y el retorno de un activo libre de riesgo es la prima de riesgo . Los datos históricos sobre retornos de los activos son una de las posibles fuentes de información sobre primas de riesgo y desviaciones estándar. Hedging El riesgo de un activo no puede ser evaluado aisladamente . A veces al agregar un activo riesgoso a un portfolio se reduce el riesgo total del portfolio. Se denomina hedging a la acción de invertir en un activo riesgoso con el objetivo de reducir el riesgo total del portfolio . 01 Conceptos Generales Riesgo

5. Existen dos actividades a la hora de invertir 1 2 Research sobre el activo y el mercado con el objetivo de determinar el riesgo y el retorno de cada activo en particular. Formación de un portfolio óptimo de activos 01 Conceptos Generales Riesgo y retorno de un activo y un portfolio

6. Portfolio combinado de activos con y sin riesgo Frontera eficiente Capital Asset Pricing Model Capital Market Line Security Market Line Arbitrage Pricing Theory Análisis de sensibilidad y escenarios 01 Conceptos Generales Riesgo: key Issues

7. 01 Conceptos Generales 02 Medición del riesgo en activos y portfolios. 03 Markowitz. Teoría de portfolios eficientes 04 Sensibilidad y Escenarios Índice

8. Probabilidad de ocurrencia Una inversión es riesgosa pues el emisor puede no pagar intereses o capital del bono o puede no cumplirse los pagos esperados en cualquier otro tipo de activo. Los posibles retornos son variables y puede asignarse una probabilidad a cada resultado La probabilidad de ocurrencia es la probabilidad de que un determinado resultado se produzca . 02 Medidas de riesgo Probabilidad de ocurrencia. Análisis histórico

9. Retorno esperado de un portfolio Es la suma ponderada de los rendimientos de cada uno de los activos por la participación en dinero sobre el valor total del portfolio Donde: R p = retorno esperado del portfolio W x = porcentaje en $ que representa la inversión del activo x sobre el valor total del portfolio R x = retorno esperado del activo x. Retorno absoluto de un activo Se mide con el desvío estándar de los retornos pasados del activo. No se trata de una medida 100% objetiva ya que entre otros factores dependerá del horizonte hacia atrás en el que se consideren las observaciones. Donde: R i = retorno del activo con probabilidad de ocurrencia i R = promedio simple del retorno. p i = probabilidad de ocurrencia del retorno i 02 Medidas de riesgo Riesgo y retorno en un activo y en un portfolio

10. Riesgo relativo de un activo Es la relación entre el riesgo (desvío estándar) y el retorno (retorno promedio). Se denomina genéricamente coeficiente de variación. Riesgo absoluto de un portfolio de 2 activos A diferencia del retorno, para la determinación del riesgo de un portfolio jamás se deben promediar los riesgos de los activos debido a la presencia de correlaciones entre ellos . Donde: σ =desvío estándar R= retorno promedio Donde : Wx = porcentaje en $ que representa la inversión del activo x sobre el valor total del portfolio σ x = desvío estándar del activo x COV a,b =covarianza entre el activo A y el activo B Ρ a,b =coeficiente de correlación entre el activo A y el activo B 02 Medidas de riesgo Riesgo y retorno en un activo y en un portfolio

11. 01 Conceptos Generales 02 Medición del riesgo en activos y portfolios. 03 Markowitz. Teoría de portfolios eficientes 04 Sensibilidad y Escenarios Índice

12. σ r CML Rf Bonds + Risky Asset Deuda + Risky Asset Portfolio A compuesto por w x X, w y Y, w z Z. Retorno A @ riesgo A Portfolio B compuesto por w m M, w n N, w q Q. Retorno B @ riesgo B Porfolio C. Máximo retorno a riesgo C Portfolio D . Máximo retorno a riesgo D. Portfolio E . Retorno E @ riesgo E. Ineficiente ya que C tiene mismo riesgo y más retorno. Portfolio F = porfolio de mercado + inversión en activo libre de riesgo. Portfolio G = portfolio de mercado + endeudamiento a tasa libre de riesgo Portfolio H : portfolio puro de mercado 03 Markowitz. Teoría de portfolios eficientes Capital Market Line (CML) - Generalidades Conjunto de Portfolios A ¿Cuál es la mejor inversión? ¿Es posible en la realidad pasar de F a G? ¿Qué efecto tiene en el mercado una suba de tasas? ? B C D E F G H

13. a) ¿Cuál será el retorno esperado y el desvío de un portfolio formado por un 110% de colocación en un activo riesgoso, cuya esperanza de retorno es del 16% y un desvio estándar del 30% ? La tasa libre de riesgo activa es del 8% y la pasiva del 5% . b) ¿En qué proporciones debe armarse el portfolio para que tenga una esperanza de retorno del 9% ? σ r CML Rf Bonds + Risky Asset Deuda + Risky Asset 03 Markowitz. Teoría de portfolios eficientes Capital Market Line (CML) – Caso I Conjunto de Portfolios A B C D E F G H

14. Los inversores obtienen portfolios eficientes al combinar activos libres de riesgo con activos riesgosos Todos los portfolios ideales estan sobre la CML y tienen una base de rendimiento mínimo igual a rf. Es necesario separar la decisión de inversión de la de financiamiento. La aversión al riesgo determina el monto de deuda a tomar/prestar La pendiente de la CML es el trade-off riesgo-retorno y es lineal σ r CML Rf Bonds + Risky Asset Deuda + Risky Asset 03 Markowitz. Teoría de portfolios eficientes Capital Market Line (CML) – Takeaways Conjunto de Portfolios A B C D E F G H

15. CAPM R e - R f = (R m - R f ) β R e = (R m - R f ) β + R f Y = ax + b La prima de riesgo de un activo es la prima de riesgo histórica del mercado y depende linealmente por la variabilidad histórica de dicho activo frente al mercado. El retorno esperado de un activo es como mínimo el retorno de un activo libre de riesgo y puede ser mayor o menor que la prima de mercado dependiendo de la variabilidad del activo frente al mercado El retorno esperado depende de la variabilidad histórica del activo frente al mercado SML 03 Markowitz. Teoría de portfolios eficientes Security Market Line (SML) - Deducción β r (R m – R f ) ¿Dónde ubicaría Rf y Rm en el eje de retorno? ¿Dónde ubicaría un activo de igual riesgo-retorno al des mercado en la SML? ¿Qué beta tendrá? ¿Dónde ubicaría un activo sub-valuado? ¿Y uno sobre-valuado? ?

16. Highlites SML Tasa libre de riesgo ( R f ) Tasa de rendimiento del mercado ( R m ) Activo C con relación riesgo-retorno adecuada y por ende con cotización eficiente. Activo D sin relación riesgo-retorno adecuada y por ende con cotización ineficiente. Activo E sin relación riesgo-retorno adecuada y por ende con cotización ineficiente 1 03 Markowitz. Teoría de portfolios eficientes Security Market Line (SML) - Deducción β r (R m – R f ) B C A D E ¿El activo D se encuentra sobre o sub valuado? ¿Y el activo E? ¿Puede subisistir dicha condición en el tiempo? ¿Mediante que proceso se corregiría? Describirlo. ?

17. 01 Conceptos Generales 02 Medición del riesgo en activos y portfolios. 03 Markowitz. Teoría de portfolios eficientes 04 Sensibilidad y Escenarios Índice

18. MARKET RISKS Tipo de cambio Tasas de interés Equity Prices Precios commodities Etc BUSINESS RISKS Economicos Reputación Supply Chain Tecnológicos Legales y regulatorios Medio ambiente Etc OPERATIONAL RISKS RRHH Procesos Sistemas Procedimientos Políticas etc RIESGO CREDITICIO Créditos por cobrar Financiamiento de proveedores Cash Management Enterprise Risks 04 Sensibilidad y Escenarios Business Risks – Enterprise Risk Management

19. Hay una realidad Futura pero Infinitas proyecciones Ninguna proyección será como la realidad Hoy hay que decidir para responder a una realidad futura incierta Es necesario proyectar el futuro para poder decidir hoy Ninguna decisión será perfecta Una decisión puede sentenciar al fracaso o al triunfo 04 Sensibilidad y Escenarios Manejo de incertidumbre con escenarios

20. ¿Qué variables son las que generan el output (VAN, TIR, EBITDA) del modelo? ¿Cómo se relacionan entre si las variables? El Excel sólo permite relaciones lineales o iteraciones mediante macros. De necesitarse relaciones complejas y/o dinámicas se debe recurrir a herramientas específicas Determinar los valores básicos de inicio para el modelo mediante research y criterio. Análisis de Sensibilidad : En forma individiual por cada variable investigar la variación porcencual qie existe en el output frente a la variación porcentual del input. Elegir las variables que son sensibles y críticas para el output. No deben ser ni menos de tres ni más de 7 u 8. Imaginar escenarios futuros con el correspondiente impacto que tendrán en cada una de las variables sensibles. Consejo: trabajar con variaciones porcentuales sobre los valores del escenario base y no con valores absolutos. (Ej: en un escenario de boom turistico los precios serán un 20% por encima del esceanrio base) Cargar en el modelo cada uno de los escenarios y ver las variaciones del output. La clave de la simulación exitosa es la iteración. 04 Sensibilidad y Escenarios Proceso de modelización de escenarios Definición de variables 1 Construcción de relación de variables 2 Construccíón de escenario base 3 Determinación de variables sensibles 4 Elección de Key drivers 5 Construcción de escenarios 6 Análisis resultados 7

21. Color azul para todas los valores inputs Color negro para los valores con fórmulas Cuando se trabaja con proyecciones, marcar en fondo gris el año base Guardar al menos los valores del escenario base Cuando se arma un modelo con proyecciones, cada hoja debe tener en la misma columna los mismos años Delimitar claramente con bordes y negritas los subtotales y totales Siempre poner puntos para separar cifras De ser posible, trabajar con números con pocas cifras y siempre formatearlos para indicar la cuantía. (K=miles; M=millones; x=veces; cualquier magnitud que sea necesaria 04 Sensibilidad y Escenarios Nociones genéricas - TIPS