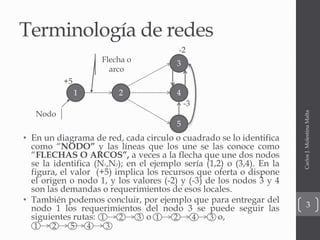
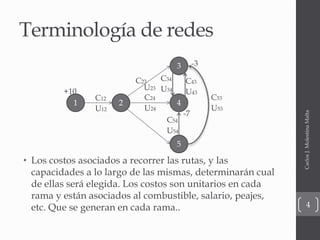
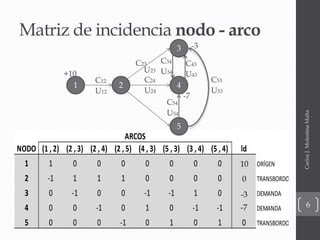
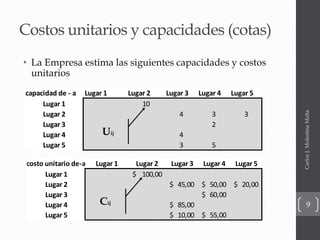
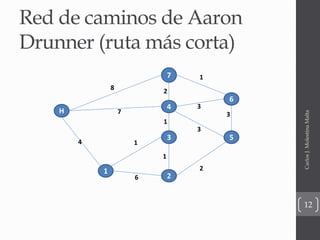
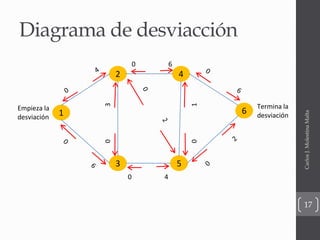
El documento presenta una introducción a diferentes modelos de optimización de redes como modelos de transbordo, ruta más corta y flujo máximo. Explica conceptos básicos como nodos, arcos, costos y capacidades. También incluye ejemplos ilustrativos de cada modelo y su formulación matemática.

1. Modelos de
optimización de redes
Volumen 5- A
Facultad de Ingeniería Industrial
Universidad de Guayaquil
CarlosJ.MolestinaMalta
1

2. Modelos de redes
• En el volumen 5, tuvimos la oportunidad de revisar,
desarrollar y aprender a interpretar modelos de
transporte y asignación, inclusive desarrollamos una red
de distribución que partía de un origen a un destino.
Estos modelos, en realidad son modelos de red
particulares.
Ahora, en este volumen (5-A) veremos sus distintas
aplicaciones generalizadas, como modelos de
“transbordo”; “ruta más corta”; “flujo máximo”. Y
aprenderemos a interpretarlos.
CarlosJ.MolestinaMalta
2

3. Terminología de redes
• En un diagrama de red, cada circulo o cuadrado se lo identifica
como “NODO” y las líneas que los une se las conoce como
“FLECHAS O ARCOS”, a veces a la flecha que une dos nodos
se la identifica (N1,N2); en el ejemplo sería (1,2) o (3,4). En la
figura, el valor (+5) implica los recursos que oferta o dispone
el origen o nodo 1, y los valores (-2) y (-3) de los nodos 3 y 4
son las demandas o requerimientos de esos locales.
• También podemos concluir, por ejemplo que para entregar del
nodo 1 los requerimientos del nodo 3 se puede seguir las
siguientes rutas: o o,
CarlosJ.MolestinaMalta
3
1 2
3
4
5
Nodo
Flecha o
arco
+5
-3
-2
1 2 3 1 2 4 3
1 2 4 35

4. Terminología de redes
• Los costos asociados a recorrer las rutas, y las
capacidades a lo largo de las mismas, determinarán cual
de ellas será elegida. Los costos son unitarios en cada
rama y están asociados al combustible, salario, peajes,
etc. Que se generan en cada rama..
CarlosJ.MolestinaMalta
4
1 2
3
4
5
+10
-7
-3
C12
U12
C23
U23
C24
U24
C34
U34
C43
U43
C54
U54
C53
U53

5. Supuestos del modelo y
propiedades de la PL
1. Cualquier planta o almacén puede enviar embarques a
cualquier otra planta o almacén.
2. Puede haber cotas (capacidades superiores o inferiores en
cada embarque (rama).
CarlosJ.MolestinaMalta
5
Propiedades:
1. Por cada arco o rama de una red, hay una variable Xij
asociada a él.
2. Por cada rama hay una ecuación de balance de flujo.
3. Los lados derechos positivos corresponden a nodos que son
proveedores netos (orígenes). Los lados derechos negativos
corresponden a nodos que son destinos netos. Los lados
derechos con valor cero corresponden a nodos que no
tienen ni oferta ni demanda (transbordo). La suma de los
términos del lado derecho es siempre cero (vertical)

6. NODO (1 , 2) (2 , 3) (2 , 4) (2 , 5) (4 , 3) (5 , 3) (3 , 4) (5 , 4) ld
1 1 0 0 0 0 0 0 0 5 ORÍGEN
2 -1 1 1 1 0 0 0 0 0 TRANSBORDO
3 0 -1 0 0 -1 -1 1 0 -2 DEMANDA
4 0 0 -1 0 1 0 -1 -1 -3 DEMANDA
5 0 0 0 -1 0 1 0 1 0 TRANSBORDO
ARCOS
10
0
-3
-7
Matriz de incidencia nodo - arco
CarlosJ.MolestinaMalta
6
1 2
3
4
5
+10
-7
-3
C12
U12
C23
U23
C24
U24
C34
U34
C43
U43
C54
U54
C53
U53

7. Formulación general del modelo de
transbordo con capacidades
𝑚𝑖𝑛𝑖𝑧𝑎𝑟
𝑖
𝑗
𝐶𝑖𝑗 𝑋𝑖𝑗
Sujeto a:
𝑋𝑖𝑗 − 𝑋𝑗𝑖 ∴ 𝑗 = 1,2,3, … 𝑛
0 ≤ 𝑋𝑖𝑗 ≤ 𝑈𝑖𝑗 𝑝𝑎𝑟𝑎 𝑡𝑜𝑑𝑜 𝑖, 𝑗 𝑑𝑒 𝑙𝑎 𝑟𝑒𝑑
CarlosJ.MolestinaMalta
7

8. Formulación del ejemplo
𝑚𝑖𝑛𝑍
= 𝐶12 𝑋12 + 𝐶23 𝑋23 + 𝐶24 𝑋24 + 𝐶25 𝑋25 + 𝐶34 𝑋34 + 𝐶43 𝑋43
+ 𝐶45 𝑋45 + 𝐶54 𝑋54 + 𝐶53 𝑋53 + 𝐶54 𝑋54
Sujeto a:
𝑋12 = 10
−𝑋12 + 𝑋23 + 𝑋24 + 𝑋25 = 0
−𝑋23 − 𝑋43 − 𝑋53 + 𝑋34 = −3
−𝑋24 + 𝑋 − 𝑋34 − 𝑋54 = −7
−𝑋25 + 𝑋53 + 𝑋54 = 0
0 ≤ 𝑋𝐼𝐽 ≤ 𝑈𝐼𝐽,
𝑇𝑂𝐷𝑂𝑆 𝐿𝑂𝑆 𝐴𝑅𝐶𝑂𝑆 𝐼𝐽 𝐷𝐸 𝐿𝐴 𝑅𝐸𝐷
CarlosJ.MolestinaMalta
8

9. Costos unitarios y capacidades (cotas)
• La Empresa estima las siguientes capacidades y costos
unitarios
CarlosJ.MolestinaMalta
9
costo unitario de-a Lugar 1 Lugar 2 Lugar 3 Lugar 4 Lugar 5
Lugar 1 100,00$
Lugar 2 45,00$ 50,00$ 20,00$
Lugar 3 60,00$
Lugar 4 85,00$
Lugar 5 10,00$ 55,00$
capacidad de - a Lugar 1 Lugar 2 Lugar 3 Lugar 4 Lugar 5
Lugar 1 10
Lugar 2 4 3 3
Lugar 3 2
Lugar 4 4
Lugar 5 3 5
Uij
Cij

10. Modelo de la ruta más corta
El Modelo de la ruta más corta, se refiere a una red en la
cual cada arco (i,j) tiene un número Cij que, en vez de ser el
costo puede ser; distancia, tiempo, costos, desde el nodo i
al nodo j. Por lo tanto una secuencia de arcos que se
conecte entre sí para unir dos arcos (inicio-final) es una
RUTA. El objetivo entonces es; encontrar la ruta más corta,
o de menor costo o más rápida desde un nodo específico
hasta cada uno de los demás nodos.
Veamos un ejemplo.
CarlosJ.MolestinaMalta
10

11. Ejemplo de ruta más corta
(extraídode “Investigacióndeoperaciones”EPPER;pág.244)
• Aaron Druner envía con frecuencia remesas de vino a
siete localidades diferentes. Aaron considera que el total
de sus costos se minimizaría si pudiera asegurarse de
que todos los envíos futuros a cualquiera de las
localidades se realicen siguiendo la ruta más corta. Por
tanto su objetivo consiste en especificar cuáles son las
rutas más cortas desde el nodo inicial hasta cualquiera de
los otros siete nodos. Observe que en este modelo, la
tarea no consiste en encontrar las Xij sino una ruta
óptima.
CarlosJ.MolestinaMalta
11

12. Red de caminos de Aaron
Drunner (ruta más corta)
CarlosJ.MolestinaMalta
12
H
1
7
4
3
2
6
5
8
7
4 1
6
2
1
1
1
3
3
2
3

13. Consideraciones del caso
Aaron
• Aquí, a diferencia de los modelos de transbordo, los
arcos no están orientados. Esto significa que en cada arco
se permite el flujo en cualquier dirección. Por supuesto,
es posible asignar una orientación a los arcos entre los
nodos, por lo cual el costo del nodo 1 al 2 es diferente al
costo del nodo 2 al 1. Esto podría ocurrir cuando el
tráfico está en la hora pico en una dirección, pero no en la
otra, o cuando la calle es de un solo sentido. Los números
que aparecen en cada arco son distancias que conectan
un nodo con otro. Aquí el punto de partida se a
designado con la letra H. En este caso Aaron está
interesado en nodo 5 y desea saber cual es la ruta más
corta.
• Sigua el caso en la hoja de excel REDES
CarlosJ.MolestinaMalta
13

14. El modelo de flujo máximo
• En el modelo de flujo máximo hay un solo nodo fuente (el nodo de
entrada) y un solo nodo recipiente o destino (el nodo de salida). La meta
consiste en encontrar la máxima cantidad de flujo total (Dinero, petróleo,
tráfico de vehículos, mensajes de internet, gas saturado, etc.) en una
unidad de tiempo.
• La cantidad de flujo por unidad de tiempo en cada arco está limitada por
restricciones de capacidad. Por ejemplo. Los diámetros de las tuberías
limitan el flujo de petróleo en las diversas partes del sintema de
distribución. También, si notamos, veremos que la capacidad en los nodos
no está especificada. Por lo que el único requisito en este caso es que para
cada nodo (a excepción de la fuente o el recipiente) la ecuación de
BALANCE DE FLUJO debe satisfacerse.
• En términos formales, si el nodo 1 (i) es la fuente y el nodo n (n) el
recipiente. El modelo es:
max 𝑓
𝑠. 𝑎.
𝑗
𝑋𝑖𝑗 −
𝐽
𝑋𝑗𝑖 =
𝑓, 𝑠𝑖 𝑖 = 1
−𝑓, 𝑠𝑖𝑖 = 𝑛
0, 𝑒𝑛 𝑜𝑡𝑟𝑎𝑠 𝑐𝑜𝑛𝑑𝑖𝑐𝑖𝑜𝑛𝑒𝑠
0 ≤ 𝑋𝑖𝑗 ≤ 𝑈𝑖𝑗 para todo (i,j) de la red
CarlosJ.MolestinaMalta
14

15. Observaciones para el modelo
de flujo máximo
1. Las variables Xij denotan el flujo por unidad de tiempo a
través del arco (i,j) que conecta el nodo i y el nodo j.
2. En la 𝑗 𝑋𝑖𝑗 es el flujo total que sale del nodo i que conecta
todos los nodos a este arco.
3. En la 𝑗 𝑋𝑗𝑖 es el flujo total que entra al nodo j que conecta
todos los nodos de entrada.
4. El símbolo f es una variable que denota el flujo total que
pasa por la red en cada unidad de tiempo. Por definición,
esto equivale al flujo por unidad de tiempo que sale de la
fuente, el nodo 1, la primera restricción. También es igual al
flujo por unidad de tiempo que entra al recipiente, nodo n
(la segunda restricción). El objetivo es maximizar esta última
cantidad.
5. Las Uij indican las capacidades de los flujos por unidad de
tiempo a través de los diversos arcos.
CarlosJ.MolestinaMalta
15

16. Caso de flujo máximo
Comisión de planeación de desarrollo
urbano
Gloria Stime está a cargo de la comisión de Planeación del
Desarrollo Urbano (UDPC por sus siglas en inglés), un
grupo de estudio ad hoc de interés especial. La
responsabilidad actual del grupo es el de coordinar la
construcción del nuevo sistema de vías subterráneas con el
departamento de mantenimiento de caminos. En virtud de
que el nuevo sistema de vía subterránea se construirá cerca
del circuito periférico de la ciudad, el tráfico de este que se
dirige al oriente deberá ser desviado. La desviación
planeada es en realidad una red de rutas alternas
propuestas por el departamento de mantenimiento de
caminos. Los diferentes límites de velocidad y los patrones
de tráfico producen distintas capacidades de flujo en los
diferentes arcos de la red propuesta de acuerdo al
siguiente diagrama.
CarlosJ.MolestinaMalta
16

17. Diagrama de desviacción
CarlosJ.MolestinaMalta
17
1
2
3
4
6
5
0 6
0 4
03
01
Empieza la
desviación
Termina la
desviación

18. Interpretación del diagrama
El nodo indica el inicio de la desviación; es decir, el
punto en el cual el tráfico que se dirigía hacia el oriente
sale de la vía periférica, El nodo es el punto en cual el
tráfico desviado entra de nuevo en la vía periférica. Vemos
también que las capacidades dependen de la dirección. Por
ejemplo 6 en el arco (1,3) equivale a 6000 vehículos por
hora en la dirección 1 – 3. En sentido contrario (3-1) es cero,
esto por lógica nos dice que es una vía de un solo sentido.
Veamos el caso en la hoja de Excel REDES
CarlosJ.MolestinaMalta
18
1
6

19. CarlosJ.MolestinaMalta
19