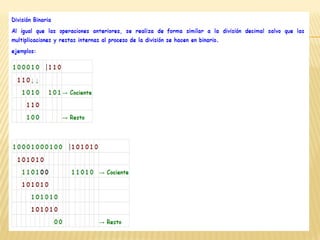
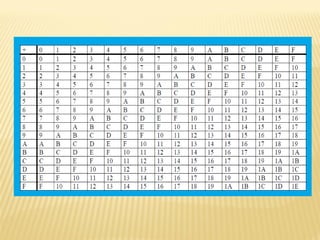
Este documento explica los procedimientos básicos para realizar operaciones aritméticas en el sistema binario, incluyendo suma, resta, multiplicación y división. Para la suma y resta binaria, se describen las cuatro posibles combinaciones (0 + 0, 0 + 1, 1 + 0, 1 + 1) y cómo se lleva a cabo la reagrupación. La multiplicación binaria implica multiplicar cada dígito del multiplicador por el multiplicando y sumar los resultados. La división binaria consiste en restar repetidamente el divisor del dividendo hasta que no quede ning

2. SUMA EN BINARIO
Para realizar la suma o adición hay que
seguir las siguientes reglas:
0 + 0 = 0 y llevamos 0.
0 + 1 = 1 y llevamos 0.
1 + 0 = 1 y llevamos 0.
1 + 1 = 0 y llevamos 1.

3.  Sumar 10112 + 1112
1 1
1100111122
11111122
110000110022
1er Orden 1 + 1 = 10 pones 0 y llevas 1
2do Orden 1 + 1+ 1 = 11 pones 1 y llevas 1
3er Orden 1 + 1 = 10 pones 0 y llevas 1
4to Orden 1 + 1 = 10
Recuérdate que la respuesta de la suma se encuentra sumando de
derecha a izquierda y poniendo al lado superior lo que llevo.

4. 4

5. Para sumar números binarios,
seguimos las reglas utilizadas
para la suma de números
decimales. La única
diferencia es que, como el
sistema binario consta de dos
caracteres, la reagrupación
de los números es más corta.
(3)1+1+1 = 11
(4)1+1+1+1 = 100
(5)1+1+1+1+1=101
(6)1+1+1+1+1+1=110
(7)1+1+1+1+1+1+1+=111
Existen cuatro posibles
combinaciones en la suma
de binarios:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10*
*Esta suma conlleva reagrupación
ya que ha alcanzado el primer
punto de rompimiento.

6. 1
1
1
1 1
1 1 1 1 0 0
1 1 1 1 0 1
1
+ 1 1 1 1 1
0 0
1
1 0
1
1
1
0
1
1 0
1. Si la cantidad de unos
es par el resultado es 0 y
se lleva un 1.
2. La cantidad de unos a llevar
debe corresponder a los
pares de unos sumados.
1

7. 1. Sumar : 1112 + 10012
a) 100002 b) 1111112
a) 1001112 b) 101002
a) 101102 b) 1111112 Como
Revisa la tabla
de la suma

8. SUSTRACCIÓN EN BINARIO
Para realizar la sustracción se deben
seguir las siguientes reglas:
0 – 0 = 0 y llevamos 0.
0 – 1 = 1 y llevamos 1.
1 – 0 = 1 y llevamos 0.
1 – 1 = 0 y llevamos 0.
UASF - Computo I

9. Para restar números binarios,
se tiene en cuenta la siguiente
tabla:
0
1 0
1
Cuando se presenta una resta 0-1, se presta
del primer dígito no-cero a la izquierda, donde
cada cero que interviene se convierte en 10,
donde: 10-1=1
0 - 0 = 0
1 - 0 = 1
1 - 1 = 0
0 - 1 = 1*
*prestando 1 de la siguiente
columna.
1 1 0 0 0 1
- 1 0 0 1 1
0
0 1 1
1
1
1 1 1 1
0
1 1
Método Estándar

10. 10

13. MULTIPLICACIÓN BINARIA
Para poder multiplicar dos números binarios
hay que seguir las siguientes reglas:
0 x 0 = 0 cero por cero es igual a cero.
0 x 1 = 0 cero por uno es igual a cero.
1 x 0 = 0 uno por cero es igual a cero.
1 x 1 = 1 uno por uno es igual a uno.
UASF - Computo I

14. 1. Se multiplica cada
digito del multiplicador
por el multiplicando.
2. Luego se suman los
resultados.
Multiplicando
1 1 1 0 1
* 1 0 1
Multiplicador
1 1 1 0 1
0 0 0 0 0
+ 1 1 1 0 1
1 0 0 1 0 0 0 1

15. 15

16. Multiplicación binaria
Se realiza similar a la
multiplicación decimal salvo
que la suma final de los
productos se hace en binario.

17. 112 x 112
10112 x 102
100112 x 1112
1010112 x 1012

18. Dividendo Divisor
 
1110111 1001
-1001
0101
-1001
0010
-1001
0010
1. Se resta el divisor de la
misma cantidad de
cifras del Dividendo
2. Por cada resta se
adiciona un uno al
Cociente y se baja la
siguiente cifra del
dividendo.
3. Si no es posible la resta
se coloca un cero en el
cociente y se baja la
siguiente cifra en el
Dividendo.
Cociente
1 1
Residuo
1
1
1
0
1

20. Te explico con un ejemplo
Dividir : 1002 entre 102
1002 102
102 10
00
Comprobando
102 x 102 = 1002

21. 21

26.  http://www.dav.sceu.frba.utn.edu.ar/homovidens/