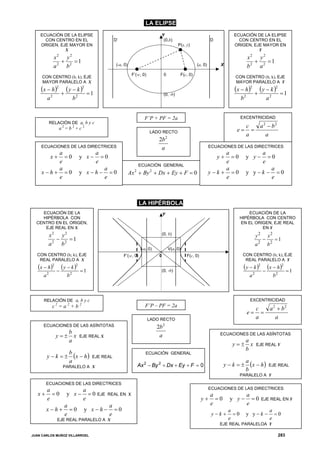
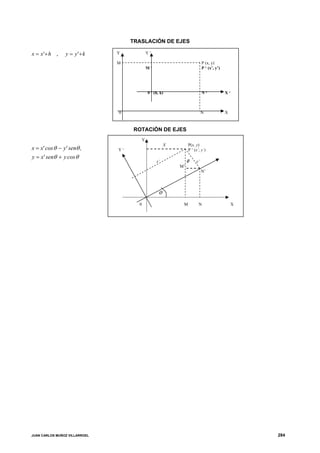
Este documento presenta las fórmulas geométricas fundamentales para calcular distancias, áreas, puntos, pendientes, ecuaciones de rectas, círculos, parábolas y elipses. Incluye ecuaciones para calcular la distancia entre dos puntos, el área de un polígono, la pendiente de una recta, la ecuación de una recta, la ecuación de un círculo, la ecuación de una parábola y una elipse, así como sus elementos como vértice, ejes, directrices y centro.

1. FORMULARIO: GEOMETRÍA ANALÍTICA
DISTANCIA ENTRE DOS PUNTOS ÁREA DE UN POLÍGONO PUNTO P (x; y) DE DIVISIÓN DE UN
P1(x1, y1); P2(x2, y2) x1 y1 SEGMENTO ENTRE P1(x1, y1) y P2(x2, y2)
d= (x2 − x1 )2 + ( y2 − y1 )2 x2 y 2 MEDIANTE UNA RAZÓN r=
PP
1
1 PP2
PENDIENTE DE UNA A= x3 y3
RECTA ENTRE P1(x1, y1) y 2 x1 + r ⋅ x2 y1 + r ⋅ y2
P2(x2, y2) x4 y 4 x= y=
1+ r 1+ r
y2 − y1
tan θ = m = x1 y1
x2 − x1
DISTANCIA DE UN PUNTO P 1 (x1, y1) ECUACIONES DE LA RECTA
A UNA RECTA Ax + By + C = 0
PENDIENTE – ORDENADA PUNTO – PENDIENTE
Ax1 + By1 + C EN EL ORIGEN y − y1 = m(x − x1 )
d=
y = mx + b
± A +B
2 2
CUANDO SE CONOCEN
ÁNGULO ENTRE DOS RECTAS L1 y L2 REDUCIDA Ó ABSCISA – DOS PUNTOS: CARTESIANA
m2 − m1 y2 − y1
ORDENADA EN EL ORIGEN
tan α = x y
+ =1
y − y1 = (x − x1 )
1 + m2 ⋅ m1 x2 − x1
a b
RECTAS PERPENDICULARES
1 ECUACIÓN NORMAL GENERAL
L1 ⊥ L2⇔ m1 = − x cos ω + ysenω − p = 0 Ax + By + C = 0
m2
RECTAS PARALELAS
L1 ‖ L2⇔ m1 = m2
CIRCUNFERENCIA
ECUACIÓN DE LA CIRCUNFERENCIA ECUACIÓN GENERAL
DE CENTRO (h, k) Y RADIO r
(x − h )2 + ( y − k )2 = r 2 x 2 + y 2 + Dx + Ey + F = 0 ⎛ D E⎞
C⎜ − , − ⎟ r =
1
D2 + E 2 − 4F
⎝ 2 2⎠ 2
ECUACIÓN DE LA CIRCUNFERENCIA Si D 2 + E 2- 4F > 0, la circunferencia es real.
DE CENTRO (0,0) Y RADIO r
Si D 2 + E 2- 4F < 0, la circunferencia es imaginaria..
x2 + y 2 = r 2
Si D 2 + E 2- 4F = 0, el radio es cero y la circunferencia
es el punto ⎛ − D ,− E ⎞
⎜ ⎟
⎝ 2 2⎠
LA PARÁBOLA
ECUACIÓN DE LA PARÁBOLA Y P(x, y) ECUACIÓN DE LA PARÁBOLA CON
CON VÉRTICE EL ORIGEN VÉRTICE EL ORIGEN
y 2 = ±4ax x 2 = ±4ay
EJE EL x EJE EL y
0 X
VÉRTICE (h, k)
(x − h )2 = ±4a( y − k )
VÉRTICE (h, k) F(a, 0)
(y − k ) 2
= ±4a(x − h )
EJE PARALELO A y
EJE PARALELO A x
ECUACIÓN DE LA DIRECTRÍZ ECUACIÓN DE LA DIRECTRÍZ
x±a=0 LADO RECTO y±a=0
x-h±a=0 4a y-k±a=0
ECUACIÓN GENERAL
y + Dx + Ey + F = 0 ; x 2 + Dx + Ey + F = 0
2
JUAN CARLOS MUÑOZ VILLARROEL 282

2. LA ELIPSE
ECUACIÓN DE LA ELIPSE Y ECUACIÓN DE LA ELIPSE
CON CENTRO EN EL D’ (0,b) D CON CENTRO EN EL
ORIGEN, EJE MAYOR EN P(x, y) ORIGEN, EJE MAYOR EN
X Y
x2 y2 x2 y 2
+ =1 + =1
a 2 b2 (-a, 0) (a, 0) X b2 a2
F’(-c, 0) 0 F(c, 0)
CON CENTRO (h; k), EJE CON CENTRO (h; k), EJE
MAYOR PARALELO A X MAYOR PARALELO A Y
(x − h )2 + ( y − k )2 =1
(x − h )2 + ( y − k )2 =1
(0, -b)
a2 b2 b2 a2
F’P + PF = 2a EXCENTRICIDAD
RELACIÓN DE a, b y c
a2 = b 2 + c 2 c a 2 − b2
LADO RECTO e= =
a a
2b 2
ECUACIONES DE LAS DIRECTRICES a ECUACIONES DE LAS DIRECTRICES
a a a a
x+ =0 y x− =0 y+ =0 y y− =0
e e e e
ECUACIÓN GENERAL
a a a a
x−h+ =0 y x−h− =0 Ax + By 2 + Dx + Ey + F = 0
2
y−k + =0 y y−k − =0
e e e e
LA HIPÉRBOLA
ECUACIÓN DE LA Y ECUACIÓN DE LA
HIPÉRBOLA CON HIPÉRBOLA CON CENTRO
CENTRO EN EL ORIGEN, EN EL ORIGEN, EJE REAL
EJE REAL EN X EN Y
x2 y2 (0, b) 2
y2
x
− =1 − =1
a2 b2 a 2
b2
(-a, 0) V(a, 0)
CON CENTRO (h; k), EJE F’(-c, 0) 0 F(c, 0) CON CENTRO (h; k), EJE
REAL PARALELO A X REAL PARALELO A Y
(x − h )2 − ( y − k )2 =1 (0, -b)
( y − k )2 − (x − h )2 =1
a2 b2 a2 b2
RELACIÓN DE a, b y c EXCENTRICIDAD
c2 = a 2 + b 2 F’P – PF = 2a
c a 2 + b2
e= =
LADO RECTO a a
ECUACIONES DE LAS ASÍNTOTAS 2b 2
b
y=± x EJE REAL X a ECUACIONES DE LAS ASÍNTOTAS
a a
y=± x EJE REAL Y
b
y−k =±
b
(x − h ) EJE REAL
ECUACIÓN GENERAL
a
PARALELO A X Ax 2 − By 2 + Dx + Ey + F = 0 y−k =±
a
(x − h ) EJE REAL
b
PARALELO A Y
ECUACIONES DE LAS DIRECTRICES
a a ECUACIONES DE LAS DIRECTRICES
x+ =0 y x− =0 EJE REAL EN X a a
e e y+ =0 y y− =0 EJE REAL EN Y
a a e e
x−h+ =0 y x−h− =0 a a
e e y−k + =0 y y−k − =0
EJE REAL PARALELO A X e e
EJE REAL PARALELOA Y
JUAN CARLOS MUÑOZ VILLARROEL 283

3. TRASLACIÓN DE EJES
x = x' + h , y = y' + k Y Y’
M P (x, y)
M‘ P ‘ (x’, y’)
0 ‘ (h, k) N‘ X‘
0 N X
ROTACIÓN DE EJES
Y
X P(x, y)
x = x' cos θ − y' senθ , Y‘ P ‘ (x‘, y‘)
y = x' senθ + y cos θ
x’ θ y’
M’
N’
Θ
0 M N X
JUAN CARLOS MUÑOZ VILLARROEL 284