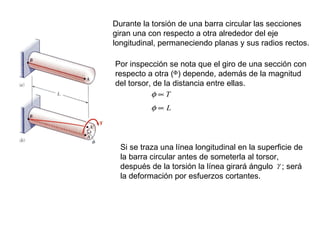
Este documento describe la torsión, que ocurre durante la transmisión de rotación a través de un eje. Explica que la torsión produce esfuerzos cortantes perpendiculares y paralelos al eje, y que estos esfuerzos causan una deformación angular en la sección transversal. También cubre la relación entre el esfuerzo cortante, el ángulo de torsión, y la distancia radial desde el eje durante la torsión elástica de una barra circular.

1. TORSIÓN Este tipo de carga es muy frecuente en ingeniería mecánica. Se da durante la transmisión de la rotación. Una turbina genera la rotación y la transmite al eje (o flecha) por medio de un momento torsor El eje transmite la rotación (por medio de momento torsor) al generador con lo que se realiza algún trabajo. Fuerza interna en el eje será torsor, lo que producirá esfuerzos cortantes que actuarán en el plano perpendicular al eje.

2. Las condiciones del equilibrio exigen que los mismos esfuerzos cortantes se presentarán en los planos perpendiculares. Esto significa que además de esfuerzos cortantes en las secciones perpendiculares al eje, habrá también esfuerzos cortantes longitudinales. Esto se puede comprobar si se tuerce una barra que resiste menos esfuerzos cortantes longitudinales que los transversales (una pieza de madera con las fibras dirigidas a lo largo de la barra). Primeras grietas aparecerán a lo largo de la barra.

3. Durante la torsión de una barra circular las secciones giran una con respecto a otra alrededor del eje longitudinal, permaneciendo planas y sus radios rectos. Por inspección se nota que el giro de una sección con respecto a otra ( ) depende, además de la magnitud del torsor, de la distancia entre ellas. Si se traza una línea longitudinal en la superficie de la barra circular antes de someterla al torsor, después de la torsión la línea girará ángulo ; será la deformación por esfuerzos cortantes.

4. Considerando una parte interna del eje del radio  y trazando un rectángulo en la superficie de este segmento cilíndrico, después de someter el eje a torsión, el rectángulo se convertirá en un romboide. Se puede establecer la siguiente relación: o Esfuerzo cortante será proporcional al ángulo de torsión  y por lo tanto al radio 

5. ESFUERZOS EN EL RANGO ELÁSTICO Multiplicando la ecuación previa con el módulo a cortante se tiene: Según Hooke Esfuerzo cortante es linealmente proporcional al posición radial del´punto. De la ecuación del equilibrio la suma de los momentos de los esfuerzos en todo el área de la sección será igual al momento torsor, El resultado se conoce como la formula de la torsión elástica,

6. Un elemento con las caras paralelas y perpendiculares al eje estará sometido a esfuerzos cortantes (elemento a ). Para una orientación de las caras diferente, en las caras se presentarán esfuerzos cortantes y también normales (elemento b ). Pero si se considera un elemento girado a 45° (elemento c ) se tiene: En el elemento a se tiene cortante puro. Note que los esfuerzos cortantes en a y los normales en c tienen la misma magnitud.

7. MODOS DE FALLA EN TORSIÓN Material dúctil generalmente falla por cortante pero material frágil es más débil a tensión y fallará por tensión. Una muestra del material dúctil se romperá a través del plano donde se dan esfuerzos cortantes máximos: en una sección perpendicular al eje. Una muestra del material frágil fallará a lo largo de un plano perpendicular al plano donde se dará la tensión máxima: a lo largo de una superficie a 45 ° (espiral) con respecto al eje.

8. Ángulo de torsión en el rango elástico En el rango elástico es valida la ley de Hook y la máxima deformación por cortante será: Viendo el dibujo se concluye la relación entre la deformación por cortante  max y el giro de la sección por torsión,  Si a lo largo de un eje el momento torsor cambia o la sección cambia, el giro de la sección se calcula por tramos y finalmente se suman todos los giros.

9. ÁRBOLES ESTATICAMENTE INDETERMINADOS Ejemplo: un árbol empotrado en los dos extremos con un momento torsor actuando en la sección B. Determinar los momentos en los extremos A y C. DCL Ecuación de equilibrio: Ecuación de la compatibilidad de las deformaciones: Sustituyendo en la ecuación de equilibrio y resolviendo:

10. PRÁCTICA: problema #1 del II ex. parcial, II ciclo 2004 La barra circular AB con extremos fijos está perforada axialmente hasta la mitad de su longitud según se muestra en la figura. ¿A que distancia ¨x¨ del extremo A debe aplicarse un par T a fin de que los pares reactivos en los soportes sean iguales? SOLUCIÓN DCL Propiedades de las secciones: Ec. de equilibrio Requisito: Compatibilidad de las deformaciones: Giro de la sección en C: donde: Igualando y arreglando: