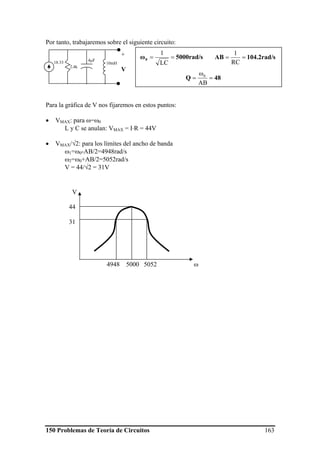
Este documento presenta 150 problemas resueltos de teoría de circuitos organizados en 5 temas:
1) Análisis de circuitos en corriente continua
2) Análisis transitorio
3) Análisis en régimen estacionario senoidal
4) Resonancia
5) Acoplamiento magnético
Cada problema está resuelto de manera detallada paso a paso para mostrar las técnicas de análisis aplicadas al tema correspondiente. Adicionalmente incluye problemas propuestos sin solución para que el lector los resuel

























































![150 Problemas de Teoría de Circuitos 58
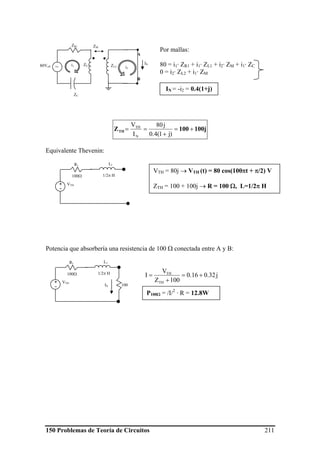
Por tanto, el equivalente Thevenin y el circuito equivalente una vez colocada la bobina
quedan:
Sobre el circuito equivalente es fácil calcular iL y vL:
[ ] τ
−
∞−+∞=
t
LLLL e)(i)0(i)(i)t(i
Donde los datos que nos hacen falta son:
5
LL 10
R
L
;mA25.1
4800
6
)(i;mA625.0)0(i −
==τ==∞−=
Con lo que la expresión de la intensidad queda:
mA1.875e1.25(t)i t10
L
5
−
−=
Se nos pide también la expresión de la tensión en la bobina, que será:
Ve9e1010875.11048
dt
)t(di
L)t(v t10t10533L
L
55
−−−−
=⋅⋅⋅⋅⋅=⋅=
V9e(t)v t10
L
5
−
=
Una representación aproximada de ambas funciones sería la siguiente:
Donde se aprecia que iL(t) no presenta saltos bruscos pero vL(t) si presenta una
discontinuidad en t = 0.
6V+
-
4.8kΩ
+ vL −
6V+
-
4.8kΩ 48mHiL
iL(t)
t
vL(t)
t](https://image.slidesharecdn.com/taller2electricidad-180418185714/85/Taller-2-electricidad-58-320.jpg)






![150 Problemas de Teoría de Circuitos 65
Obtener la expresión de la tensión v(t) del condensador en el circuito de la figura:
Dato v(0) = 0V.
Mediante sucesivas transformaciones de fuentes se obtiene el siguiente circuito
equivalente:
Obtendremos la expresión de v(t) a partir del valor inicial, el valor final y la constante
de tiempo:
• Valor inicial: v(0) = 0V
• Valor final: v(∞) = 2V
• Cte. de tiempo: τ = RC = 0,064seg
Septiembre 2001
PROBLEMA 25:
SOLUCIÓN 25:
6Ω
20V+
-
2Ω4Ω
2A
+ -
10V
2Ω
10mF
+ v(t) -
6,4Ω
2V-
+
10mF
_
v(t)
+
( ) ( ) ( ) ( )[ ] ( )Ve12tv t15,625⋅−τ
−
−⋅=⋅−∞−∞=
t
e0vvv](https://image.slidesharecdn.com/taller2electricidad-180418185714/85/Taller-2-electricidad-65-320.jpg)


















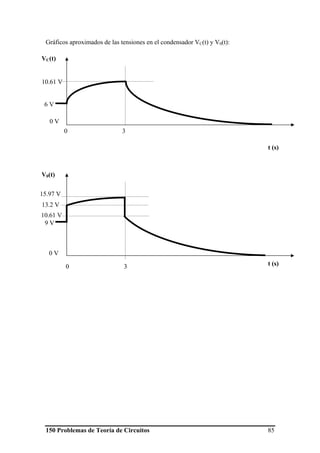








![150 Problemas de Teoría de Circuitos 94
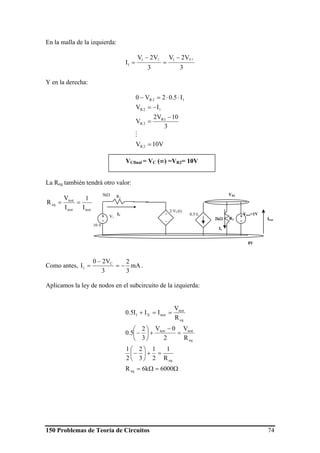
En el gráfico se aprecian los dos transitorios que ocurren en el circuito durante el
intervalo de tiempo considerado: durante el primer transitorio el condensador se carga
pasando a valer su tensión de 0 a 6V, y en el segundo transitorio se descarga hasta 2V.
1º transitorio: carga del C de 0 a 6V (S1 se cierra en t = 0, t∈[0 ,40s])
Del gráfico se deduce que VCinicial = 0 y VCfinal = 6V, y con el dato del valor de VCfinal se
calcula el valor de R1.
Se simplifica el circuito anterior hallando el circuito equivalente Thévenin entre los
terminales de R1. La RTH es igual al equivalente serie de las dos resistencias de 1kΩ, es
decir, RTH = 2 kΩ. Y VTH se obtiene fácilmente utilizando la ley de Ohm sobre una de
las resistencias de 1kΩ, siendo VTH = 12V. De forma que el circuito anterior se reduce
a:
Sabiendo queVCfinal = 6V, se obtiene R1
→
+
=
1
1
Cfinal
R2
R
12V
El valor de la capacidad del condensador se obtiene a partir del dato de la constante de
tiempo del transitorio ( τ =RC) que se deduce a su vez del gráfico: el valor de τ es el
instante en que la pendiente en el origen corta a la asíntota del valor final de la tensión,
luego τ = 8s.
SOLUCIÓN 33:
3kΩ
12mA
1kΩ
R1
C
+
Vc
-
1kΩ
S1
2kΩ
R1
C
+
Vc
-
S1
12V+
-
VCfinal
R1 = 2kΩ
2kΩ
R1
C
+
Vc
-
S1
12V+
-
2kΩ
1kΩ
C
+
Vc
-
S1
12V+
-
2k paralelo 2k = 1k](https://image.slidesharecdn.com/taller2electricidad-180418185714/85/Taller-2-electricidad-94-320.jpg)
![150 Problemas de Teoría de Circuitos 95
8C·10·1
s8RC
3
==τ
==τ
2º transitorio: descarga del C de 6 a 2V (S1 se abre y S2 se cierra en t = 40, t∈[40 ,∞])
Del gráfico se deduce que VCfinal = 2V, por tanto
El valor de τ para este transitorio es también el instante en que la pendiente en el origen
corta a la asíntota del valor final de la tensión, luego para este 2º transitorio τ = 8s. (en
el gráfico 48s, pero como el intervalo considerado comienza en 40s, 48-40 = 8s) y con
el dato de τ = 8s se halla el valor de R2:
810·8·R
s8CR
3
2
2
==τ
==τ
−
C = 8mF→
C
+
Vc
-
R2
Vg+
-
S2
Vg = VCfinal = 2V
R2 = 1kΩ
→](https://image.slidesharecdn.com/taller2electricidad-180418185714/85/Taller-2-electricidad-95-320.jpg)