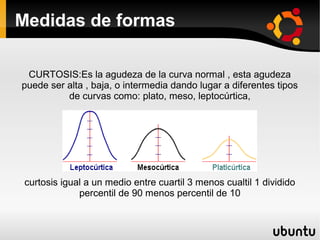
Este documento describe diferentes parámetros estadísticos como medidas de centralización (medias, moda y mediana), medidas de posición (cuartiles, deciles y centiles), medidas de dispersión (rango, desviación típica y varianza) y medidas de forma (sesgo y curtosis). También explica conceptos como la interpretación de la media y la desviación típica, la desigualdad de Chebycheff, la transformación de datos estadísticos y el coeficiente de variación.

1. PARÁMETROS ESTADÍSTICOS
* Medidas de Centralización: Medias, moda y
Mediana
* Medidas de
Posición:Cuartiles,Deciles,Centiles
* Medidas de Dispersión: Rango, rango
intercuartílico,Desviación media, varianza,
desviación típica.
* Medidas de Forma: coeficiente de
apuntamiento,coeficiente de asimetría (curtosis)

2. MEDIDAS DE CENTRALIZACIÓN
Media:
-Media aritmética:La media aritmética de una variable se define como la suma
ponderada de los valores de la variable por sus frecuencias relativas y lo
denotaremos por x,y.
Fórmula:
-Media geométrica:La media geométrica de N observaciones es la raíz de
índice N del producto de todas las observaciones. La representaremos por G.
Fórmula:
-Media armónica:La media armónica de N observaciones es la inversa de la
media de las inversas de las observaciones y la denotaremos por H.
Fórmula:

3. MEDIDAS DE CENTRALIZACIÓN
Moda:La moda es el valor de la variable que
tenga mayor frecuencia absoluta, la que más se
repite.
Para calcular la moda en el caso de que la
variable sea continua, utilizamos la siguiente
fórmula:

4. MEDIDAS DE CENTRALIZACIÓN
Mediana:es el valor central de la variable, es decir, supuesta la
muestra ordenada en orden creciente o decreciente, el valor que
divide en dos partes la muestra.
Cálculo de la mediana en el caso discreto:
Tendremos en cuenta el tamaño de la muestra.
Si N es Impar, hay un término central, el término que será el valor
de la mediana.
Si N es Par, hay dos términos centrales, la mediana será la media
de esos dos valores (...)

5. Medidas de centralización
(...)Cálculo de la mediana en el caso continuo:
Si la variable es continua, la tabla vendrá en
intervalos, por lo que se calcula de la siguiente
forma:

6. Medidas de posición
Son indicadores usados para señalar que
porcentaje de datos dentro de una distribución de
frecuencias superan estas expresiones, cuyo
valor representa el valor del dato que se
encuentra en el centro de la distribución de
frecuencia.

7. Medidas de posición
Cuartiles (Q1, Q2,Q3)
*Fórmula de Q1 para series de Datos Agrupados
en Clase.
*Fórmula de Q3 para series de Datos Agrupados
en Clase.

8. Medidas de posición
Deciles.
Fórmula para calcular deciles de forma continua.
Ejemplos:

9. Medidas de posición
Centiles: Se denomina Centil o Percentil la
puntuación que deja por bajo el k por ciento de
las puntuaciones de una distribución.
Fórmula:

10. Medidas de dispersión
Las medidas de dispersión nos informan sobre cuánto se alejan del centro los
valores de la distribución.
* Rango:El rango es la diferencia entre el mayor y el menor de los datos de una
distribución estadística.
* Rango intercuartílico: 􀁼 Es la diferencia entre el Q1 y el Q3
Nos indica la dispersión en el 50% central de la distribución
Es más sensible a la concentración de los datos que el
recorrido ordinario
Su cálculo es indistinto para datos originales como para datos
agrupados.
RI =Q3 −Q1

11. Medidas de dispersión
Desviacion media:La desviación respecto a la media es la
diferencia entre cada valor de la variable estadística y la media
aritmética.
Varianza: es la media aritmética del cuadrado de las
desviaciones respecto a la media de una distribución
estadística.

12. Medidas de dispersión
La desviación típica es la raíz cuadrada de la
varianza.

13. Medidas de formas
EL SESGO:Mide las desviaciones de las MTC., Ya que el seesgo es el
grado de asimetría o falta de asimetría, de una distribucion, si el
poligono de frecuencias visualizado de una distribucion tiene una cola
más larga a la derecha del máximo central que a la izquierda, se dice
que la distribucion esta sesgada a la derecha o que tiene sesgo
positivo(asimetría positiva) y si al contrario se dice que tiene sesgo
(asimetría negativa) en la asimetria encontramos si es:
Sg= __X -Md__ = Sesgo es igual a: media menos la moda partido o
dividido desviacion.
S
los datos más utilizados son los sig:
moda , media, desviación.

14. Medidas de formas
CURTOSIS:Es la agudeza de la curva normal , esta agudeza
puede ser alta , baja, o intermedia dando lugar a diferentes tipos
de curvas como: plato, meso, leptocúrtica,
curtosis igual a un medio entre cuartil 3 menos cualtil 1 dividido
percentil de 90 menos percentil de 10

15. Interpretacion de la media y la
desviacion tipica
Interpretacion de la media: se aplica a aquellas situaciones en
las que la media aritmética se calcula para un subconjunto de la
población objeto de estudio.
La media muestral es un parámetro de extrema importancia en
la inferencia estadística, siendo de gran utilidad para la
estimación de la media poblacional, entre otros usos.
La desviación estándar puede ser interpretada como una medida
de incertidumbre. La desviación estándar de un grupo repetido
de medidas nos da la precisión de éstas. Cuando se va a
determinar si un grupo de medidas está de acuerdo con el
modelo teórico, la desviación estándar de esas medidas es de
vital importancia: si la media de las medidas está demasiado
alejada de la predicción (con la distancia medida en
desviaciones estándar), entonces consideramos que las
medidas contradicen la teoría.

16. Desigualdad de TCHEBYCHEFF
En probabilidad, la desigualdad de Chebyshov (también
escrito como "Tchebycheff") es un resultado que ofrece
una cota inferior a la probabilidad de que el valor de una
variable aleatoria con varianza finita esté a una cierta
distancia de su esperanza matemática. La desigualdad
recibe su nombre del matemático ruso Pafnuti Chebyshov
.
*Sea variable aleatoria con momento de orden finito,
entonces

17. Transformación de datos
estadisticos
la transformación de datos se efectúa para asegurarse así de que
tienen una distribución normal (un remedio para los valores atípicos
, fallas de la normalidad, la linealidad, y homocedasticidad), lo que
normalmente se hace para preparar los datos para el análisis de
regresión,[1] ya que este análisis asume los datos son lineales,
normales y homoscedásticos. Esto también se conoce como la
transformación de la linealidad. Un buen indicador de los datos con
una distribución normal es el sesgo en el rango de -0,8 a 0,8 y
curtosis en el rango de -3,0 a 3,0.
Pequeñas muestras de una de población con valores atípicos son
un problema, porque los intervalos de confianza que producen a
menudo están fuera de centro y son muy estrechos. El intervalo de
confianza será mayor que la tasa de captura de estos intervalos. Si
el tamaño de la muestra es demasiado pequeña o los datos están
sesgados se puede intentar una de estas transformaciones:
logarítmica, raíz cuadrada o inversa.

18. Coeficiente de Variación
Su fórmula expresa la desviación estándar como porcentaje de la
media aritmética, mostrando una mejor interpretación porcentual del
grado de variabilidad que la desviación típica o estándar. Por otro
lado presenta problemas ya que a diferencia de la desviación típica
este coeficiente es variable ante cambios de origen. Por ello es
importante que todos los valores sean positivos y su media dé, por
tanto, un valor positivo. A mayor valor del coeficiente de variación
mayor heterogeneidad de los valores de la variable; y a menor C.V.,
mayor homogeneidad en los valores de la variable. Suele
representarse por medio de las siglas C.V.
*Se calcula: