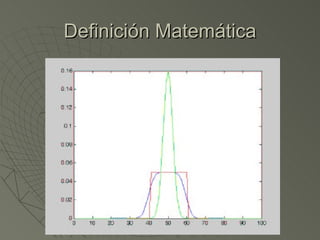
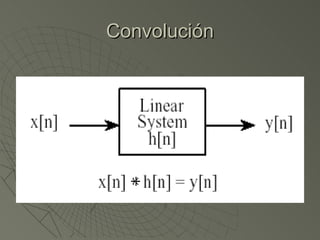
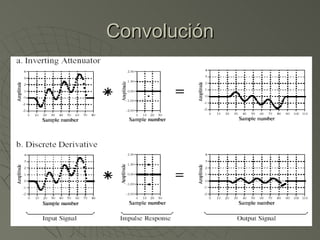
El documento explica la convolución, que es una operación matemática que relaciona la señal de entrada, la respuesta a impulso y la señal de salida de un sistema lineal. La convolución se calcula multiplicando cada muestra de la señal de entrada por la respuesta a impulso y sumando los resultados, ya sea de forma digital mediante una suma o de forma analógica mediante una integral. El documento también describe algoritmos para calcular la convolución desde la entrada o desde la salida y las definiciones matemáticas de la convolución en el dominio

1. Convolución http://www.fiec.espol.edu.ec

2. ¿Qué veremos hoy? Funcion Delta y Respuesta a Impulso Definición de Convolución Algoritmo desde la Entrada Algoritmos desde la Salida Definición matemática (Digital) Definición matemática (Analógico)

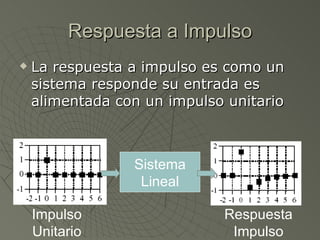
3. Respuesta a Impulso Cualquier señal puede ser descompuesta en impulsos Un impulso es una señal compuesta de ceros excepto en un punto en que tiene un valor no cero Un impulso normalizado o impulso unitario tiene el valor de uno en la muestra 0, se representa con  [n].

4. Respuesta a Impulso La respuesta a impulso es como un sistema responde su entrada es alimentada con un impulso unitario Sistema Lineal Impulso Unitario Respuesta Impulso

5. Respuesta a Impulso Si dos sistemas son diferentes de alguna manera, tendrán diferente respuesta a impulso La respuesta impulso se representa con h[n]

6. Respuesta a Impulso Cualquier impulso puede ser representado por un impulso unitario desplazado y escalado 4  [n-5] es un impulso cuya muestra número 5 tiene un valor de 4 y el resto de muestras valen 0

7. Respuesta a Impulso Si sabemos que la respuesta a impulso de un sistema lineal es h[n], ¿cual será la salida si la entrada es b  [n-a]? ¿Porqué?

8. Respuesta a Impulso La salida sería bh[n-a] Porque aplicamos las propiedades de homogeneidad e invariabilidad en el tiempo b  [n-a] bh[n-a]

9. Convolución Si una función puede ser descompuesta en impulsos, Si la respuesta a cualquier impulso es la respuesta al impulso unitario desplazada y escalada y Si la sumando las componentes de salida puedo obtener la salida total Entonces si conocemos la respuesta a impulso... ¡¡¡Lo conocemos todo sobre el sistema!!! Porque podemos saber la repuesta del sistema a cualquier señal

10. Convolución Es una operación matemática en la cual tomamos dos señales y producimos una tercera De la misma manera que en multiplicación tomamos dos número y producimos un tercero

11. Convolución En sistemas lineales, la convolución brinda una manera de relacionar 3 señales: la señal de entrada, la respuesta a impulso y la señal de salida La señal de entrada convolucionada con la respuesta a impulso es igual a la señal de salida La convolución se representa con *

12. Convolución

13. Convolución

14. Convolución

15. Convolución Ahora que sabemos que representa la convolución en sistemas lineales vamos a ver como se calcula Hay dos formas de verlo, desde la entrada o desde la salida El primero nos permite ver de una manera conceptual la convolución, el otro es la definición matemática

16. Algoritmo desde la Entrada Usamos el mismo concepto de descomposición en impulsos Tomamos cada muestra y la vamos pasando por el sistema Al final sumamos todas las salidas Asi obtenemos la salida total, o sea la covolución de la entrada con la respuesta a impulso

17. Algoritmo desde la Entrada

20. Algoritmo desde la Entrada Se puede pensar como que cada punto en la entrada contribuye a varios puntos en la salida Siempre vamos a tener N + M muestras en la salida

21. Algoritmo desde la Salida En el anterior punto de vista, vemos como una muestra en la entrada contribuye a la salida Ahora veremos lo contrario, veremos como cada muestra en la salida es influenciada por varias muestras en la entrada Hacemos esto porque matemática y computacionalmente es la forma tradicional de resolver problemas

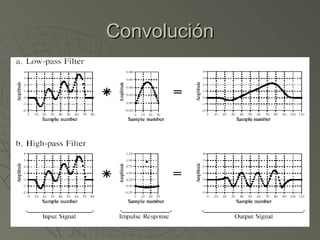
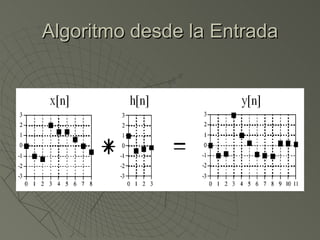
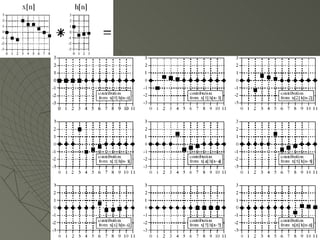
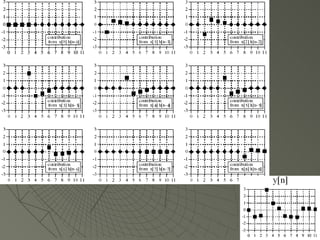
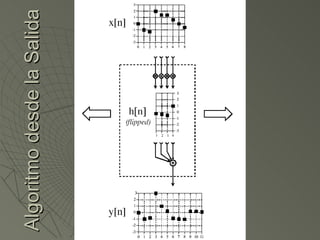
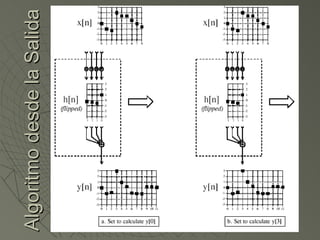
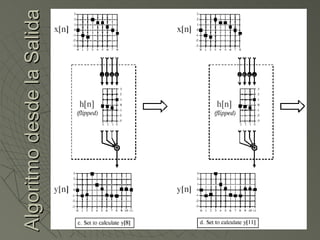
22. Algoritmo desde la Salida Viendo el ejemplo anterior para saber cuanto vale y[6] tenemos que ver muestras en la entrada producen valores no cero en y[6] y[6]=x[3]h[3]+x[4]h[2]+x[5]h[1]+x[6]h[0] Para verlo mejor usaremos la “máquina de convolución”

23. Algoritmo desde la Salida

24. Algoritmo desde la Salida

25. Algoritmo desde la Salida

26. Algoritmo desde la Salida Vemos que para los extremos tenemos que rellenar la señal de entrada con 0s Los puntos iniciales y finales contienen menos información que los puntos intermedios Se dice que la respuesta a impulso no esta totalmente inmersa en la señal de entrada

27. Algoritmo desde la Salida Es por eso que en una señal convolucionada generalmente descartamos el primer y último pedazo

28. Definición Matemática Si transladamos a una fórmula el funcionamiento de la “maquina” tenemos

29. Definición Matemática Esta sumatoria se conoce como suma de convolución o simplemente como convolución Cada punto en la salida puede ser calculado independientemente

30. Definición Matemática En pocas palabras podemos decir que convolución en el ambito digital es multiplicar cada muestra de la primera señal por toda la segunda señal y luego sumar todos esos resultados

31. Definición Matemática En el ambito continuo seguimos el mismo razonamiento. Multiplicamos cada punto de una primera señal por toda la segunda señal y luego sumamos. En continuo cuando queremos sumar todos los puntos usamos una integral

32. Definición Matemática

33. Definición Matemática

34. ¿Qué veremos hoy? Funcion Delta y Respuesta a Impulso Definición de Convolución Algoritmo desde la Entrada Algoritmos desde la Salida Definición matemática (Digital) Definición matemática (Analógico)

35. Próxima Clase Viernes 13 de Junio: Propiedades de la Convolución