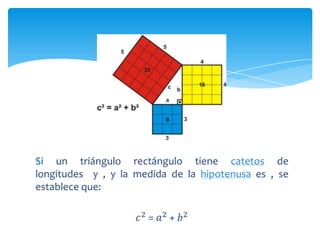
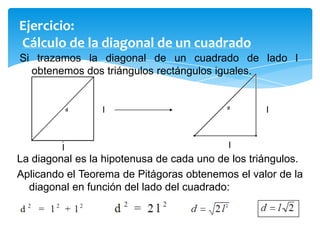
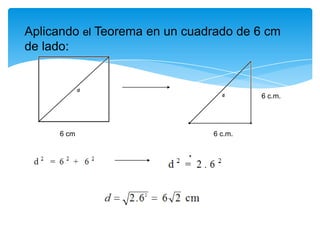
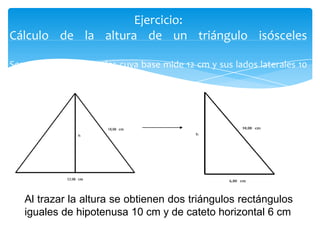
El documento describe el teorema de Pitágoras, que establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Luego presenta algunas aplicaciones prácticas del teorema, como determinar la altura de un edificio o una escalera para alcanzar frutos de un árbol. Finalmente, incluye dos ejercicios de cálculo que aplican el teorema para hallar la diagonal de un cuadrado y la altura de un triángulo isós

1. Normalista:
Mariano Martínez Loredo
Asignatura:
Procesos cognitivos y cambio
conceptual en las matemáticas

2. Tema a estudiar: teorema de
Pitágoras

3. TEOREMA DE PITÁGORAS
El teorema de Pitágoras establece que en todo triángulo
rectángulo, el cuadrado de la hipotenusa ("el lado de mayor
longitud del triángulo rectángulo") es igual a la suma de los
cuadrados de los catetos (los dos lados menores del triángulo,
los que conforman el ángulo recto).

4. Teorema de Pitágoras
En
todo
triángulo
rectángulo el cuadrado de
la hipotenusa es igual a la
suma de los cuadrados de
los catetos.
Pitágoras de Samos

5. APLICACIONES DEL TEOREMA
El teorema de Pitágoras es de
mucha utilidad en la resolución
de problemas de la vida
cotidiana.
Por ejemplo: El famoso Galileo
Galilei, utilizó el teorema de
Pitágoras para determinar la
medida de algunas montañas
lunares.

6. Conocer la altura de un
edificio, sabiendo la medida
de la sombra que proyecta y
la distancia del punto más
alto del edificio al extremo
de la sombra.

7. Se desean bajar frutos de un árbol
de naranjas, para ello se quiere
construir una escalera que sea
capaz de alcanzarlos, sabiendo la
altura a la que se encuentran los
frutos y la distancia del árbol a la
base de la escalera.

9. Ejercicio:
Cálculo de la diagonal de un cuadrado
Si trazamos la diagonal de un cuadrado de lado l
obtenemos dos triángulos rectángulos iguales.
l
l
l
l
La diagonal es la hipotenusa de cada uno de los triángulos.
Aplicando el Teorema de Pitágoras obtenemos el valor de la
diagonal en función del lado del cuadrado:

10. Aplicando el Teorema en un cuadrado de 6 cm
de lado:
6 c.m.
6 cm
6 c.m.

11. Ejercicio:
Cálculo de la altura de un triángulo isósceles
Sea un triángulo isósceles cuya base mide 12 cm y sus lados laterales 10
cm.
Al trazar la altura se obtienen dos triángulos rectángulos
iguales de hipotenusa 10 cm y de cateto horizontal 6 cm

12. La altura del triángulo es uno de los catetos.
Aplicando el Teorema de Pitágoras: