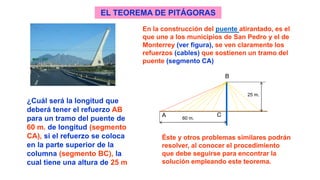
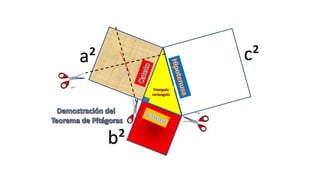
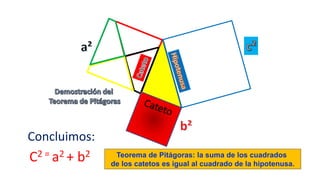
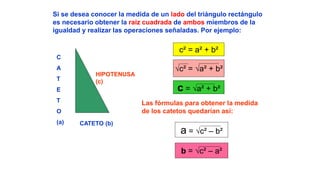
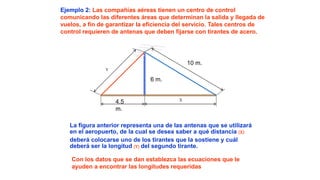
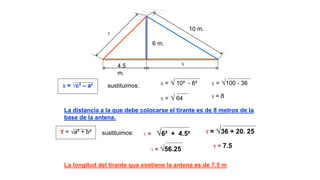
Este documento describe un modelo inductivo de enseñanza para ayudar a los estudiantes a comprender la relación entre las áreas de los cuadrados construidos sobre los lados de un triángulo rectángulo y aplicar el teorema de Pitágoras para resolver problemas. Bajo este modelo, los estudiantes siguen instrucciones paso a paso para descubrir por sí mismos estas relaciones y cómo usar el teorema. El documento proporciona ejemplos de problemas y sus soluciones usando el teorema de Pitágoras.

1. MODELO INDUCTIVO DE
ENSEÑANZA
Aprendizajes esperados:
• Resuelve problemas que implican el uso del teorema de Pitágoras.
Ejes: Forma, espacio y medida
Temas y contenidos:
 Análisis de las relaciones entre las áreas de los cuadrados que se
construyen sobre los lados de un triángulo rectángulo.
 Explicitación y uso del teorema de Pitágoras.

2. DESCRIPCIÓN DE LA PROBLEMÁTICA
A los alumnos se les dificulta comprender la relación que existen entre las áreas de los
cuadrados construidos sobre los lados de un triángulo rectángulo, además de
encontrar una aplicación en la vida real del teorema de Pitágoras.
PROPUESTA DE SOLUCIÓN
Aplicar el modelo inductivo de enseñanza en este contenido programático con el fin de
que el alumno llegue por si mismo a la conclusión de cuál es la relación entre las áreas
de los cuadrados formados en los lados de un triángulo rectángulo, para ello deben
seguir una serie de instrucciones para demostrar de una manera física y más clara el
Teorema de Pitágoras.
GRADO: TERCERO SEGUNDO TRIMESTRE
EJE: Forma Espacio y Medida
Propósito; Utilicen el teorema de Pitágoras, los criterios de congruencia y semejanza,
las razones trigonométricas y el teorema de Tales, al resolver problemas.

3. En la construcción del puente atirantado, es el
que une a los municipios de San Pedro y el de
Monterrey (ver figura), se ven claramente los
refuerzos (cables) que sostienen un tramo del
puente (segmento CA)
¿Cuál será la longitud que
deberá tener el refuerzo AB
para un tramo del puente de
60 m. de longitud (segmento
CA), si el refuerzo se coloca
en la parte superior de la
columna (segmento BC), la
cual tiene una altura de 25 m
EL TEOREMA DE PITÁGORAS
B
A C60 m.
25 m.
Éste y otros problemas similares podrán
resolver, al conocer el procedimiento
que debe seguirse para encontrar la
solución empleando este teorema.

4. Teorema:
Pitágoras: filósofo y matemático griego
que vivió en el año 582- 500 a. C.
Para hacer la demostración del teorema de
Pitágoras puede hacerse por
descomposición y equivalencia de áreas,
para ello seguirán las instrucciones que ya
tienen en sus manos.
es una proposición que puede ser
demostrada.

5. c²
b²
a²

6. Concluimos:
C2 = a2 + b2 Teorema de Pitágoras: la suma de los cuadrados
de los catetos es igual al cuadrado de la hipotenusa.

7. c² = a² + b²
√c² = √a² + b²
c = √a² + b²
a = √c² – b²
b = √c² – a²
C
A
T
E
T
O
(a) CATETO (b)
HIPOTENUSA
(c)
Si se desea conocer la medida de un lado del triángulo rectángulo
es necesario obtener la raíz cuadrada de ambos miembros de la
igualdad y realizar las operaciones señaladas. Por ejemplo:
Las fórmulas para obtener la medida
de los catetos quedarían así:

8. Ahora volvemos al ejemplo inicial y traten de resolverlo
¿Cuál será la longitud que
deberá tener el refuerzo AB para
un tramo del puente de 60 m. de
longitud (segmento CA), si el
refuerzo se coloca en la parte
superior de la columna
(segmento BC), la cual tiene una
altura de 25 m
B
A C60 m.
25 m.
C = √a² + b² sustituimos:
C = √ 60² + 25² C = √3600 + 625
C = √ 4225 C = 65
La longitud del cable AB es de 65 metros.

9. Ejemplo 2: Las compañías aéreas tienen un centro de control
comunicando las diferentes áreas que determinan la salida y llegada de
vuelos, a fin de garantizar la eficiencia del servicio. Tales centros de
control requieren de antenas que deben fijarse con tirantes de acero.
10 m.
4.5
m.
X
6 m.
Y
La figura anterior representa una de las antenas que se utilizará
en el aeropuerto, de la cual se desea saber a qué distancia (X)
deberá colocarse uno de los tirantes que la sostiene y cuál
deberá ser la longitud (Y) del segundo tirante.
Con los datos que se dan establezca las ecuaciones que le
ayuden a encontrar las longitudes requeridas

10. 10 m.
4.5
m.
X
6 m.
Y
X = √c² – a² sustituimos: X = √ 10² - 6² X = √100 - 36
X = √ 64 X = 8
La distancia a la que debe colocarse el tirante es de 8 metros de la
base de la antena.
Y = √a² + b² sustituimos:
Y = 7.5
La longitud del tirante que sostiene la antena es de 7.5 m
Y = √6² + 4.5² Y = √36 + 20. 25
Y = √56.25

11. Enseguida van a resolver los tres ejemplos que
vienen en su libro de texto, en la página 72
(Práctica guiada)
El docente evalúa las habilidades y actitudes
Punto final: Tarea (Práctica independiente), se
evalúa la adquisición de conocimientos en la
resolución de problemas