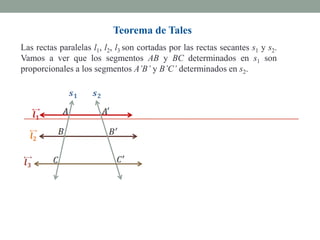
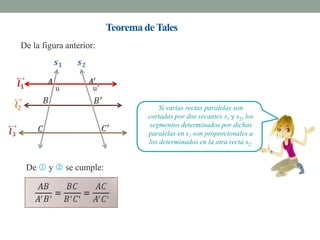
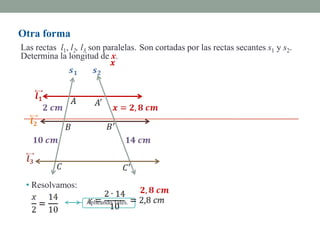
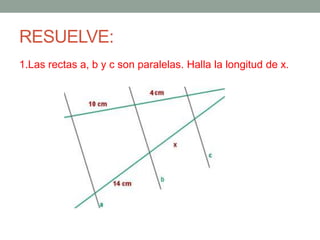
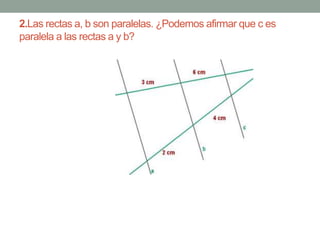
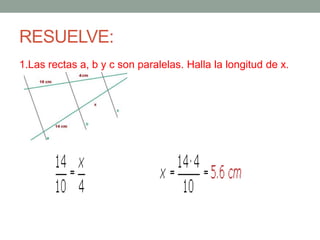
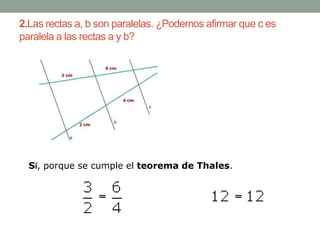
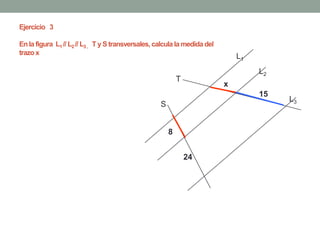
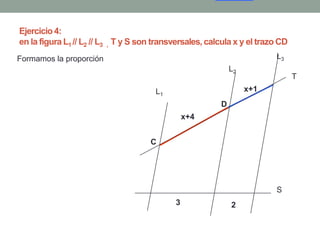
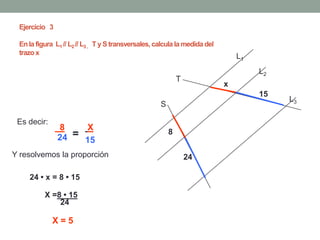
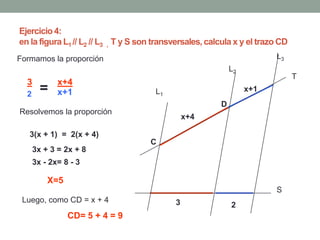
El Teorema de Tales establece que si varias rectas paralelas son cortadas por dos secantes, los segmentos determinados por dichas paralelas en una secante son proporcionales a los segmentos determinados en la otra secante. El teorema puede utilizarse para resolver problemas geométricos encontrando longitudes desconocidas mediante la formación y resolución de proporciones.

1. TEOREMA DE THALES

2. Teorema de Tales
Las rectas paralelas l1, l2, l3 son cortadas por las rectas secantes s1 y s2.
Vamos a ver que los segmentos AB y BC determinados en s1 son
proporcionales a los segmentos A’B’ y B’C’ determinados en s2.

3. Teorema de Tales
De la figura anterior:
u u’
Si varias rectas paralelas son
cortadas por dos secantes s1 y s2, los
segmentos determinados por dichas
paralelas en s1 son proporcionales a
los determinados en la otra recta s2.
De  y  se cumple:

4. Ejemplo
Las rectas l1, l2, l3 son paralelas. Son cortadas por las rectas secantes s1 y s2.
Determina la longitud de x.
Aplicando Tales
• Resolvamos:

5. Otra forma
Las rectas l1, l2, l3 son paralelas. Son cortadas por las rectas secantes s1 y s2.
Determina la longitud de x.
• Resolvamos:
Aplicando Tales.

6. TEOREMA DE THALES
EJERCICIOS

7. RESUELVE:
1.Las rectas a, b y c son paralelas. Halla la longitud de x.

8. 2.Las rectas a, b son paralelas. ¿Podemos afirmar que c es
paralela a las rectas a y b?

9. RESPUESTAS

10. RESUELVE:
1.Las rectas a, b y c son paralelas. Halla la longitud de x.

11. 2.Las rectas a, b son paralelas. ¿Podemos afirmar que c es
paralela a las rectas a y b?
Sí, porque se cumple el teorema de Thales.

12. EJERCICIOS

13. Ejercicio 3
En la figura L1 // L2 // L3 , T y S transversales, calcula la medida del
trazo x
L1
L2
T
x
15
L3
S
8
24

14. Ejercicio 4:
en la figura L1 // L2 // L3 , T y S son transversales, calcula x y el trazo CD
Formamos la proporción L3
L2
T
L1 x+1
D
x+4
C
S
3 2

15. RESPUESTAS

16. Ejercicio 3
En la figura L1 // L2 // L3 , T y S transversales, calcula la medida del
trazo x
L1
L2
T
x
15
L3
S
Es decir:
8 X 8
24 = 15
Y resolvemos la proporción 24
24 • x = 8 • 15
X =8 • 15
24
X=5

17. Ejercicio 4:
en la figura L1 // L2 // L3 , T y S son transversales, calcula x y el trazo CD
Formamos la proporción L3
L2
T
3 x+4
2
= x+1 L1 x+1
D
Resolvemos la proporción
x+4
3(x + 1) = 2(x + 4)
C
3x + 3 = 2x + 8
3x - 2x= 8 - 3
X=5
S
Luego, como CD = x + 4 3 2
CD= 5 + 4 = 9