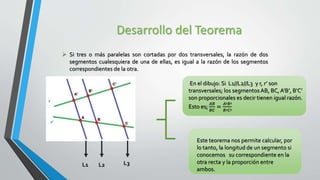
Tales de Mileto vivió en el siglo VII a.C. y fue uno de los Siete Sabios de Grecia. Se le atribuye el descubrimiento del teorema que lleva su nombre, el Teorema de Tales, el cual establece que si tres o más rectas paralelas son cortadas por dos transversales, los segmentos correspondientes tienen una razón igual. El teorema permite calcular la longitud de un segmento desconocido si se conocen las medidas de los segmentos correspondientes en otra recta paralela.

2. Un poco de historia
• Tales nació alrededor del año 640
AC en Mileto, Asia Menor (ahora
Turquía).
• Era un hombre que se destacó en
varias áreas: comerciante, hábil en
ingeniería, astrónomo, geómetra
• Se le incluye entre los Siete
Sabios.
• A él se le deben gran
cantidad de
descubrimientos
importantes, pero sobre
todo uno: el teorema
que lleva su nombre:
TEOREMA DETHALES

3. ORIGEN DEL TEOREMA DE THALES

4. Desarrollo del Teorema
 Si tres o más paralelas son cortadas por dos transversales, la razón de dos
segmentos cualesquiera de una de ellas, es igual a la razón de los segmentos
correspondientes de la otra.
L1 L2 L3
En el dibujo: Si L1//L2//L3 y r, r’ son
transversales; los segmentosAB, BC, A’B’, B’C’
son proporcionales es decir tienen igual razón.
Esto es;
𝐴𝐵
𝐵𝐶
=
𝐴′𝐵′
𝐵′𝐶′
Este teorema nos permite calcular, por
lo tanto, la longitud de un segmento si
conocemos su correspondiente en la
otra recta y la proporción entre
ambos.

5. EJEMPLOS:
1) En la figura L1 // L2 // L3 T y S transversales,
calcula la medida del trazo x.
Resolución:
Ordenamos los datos en la proporción de acuerdo al
teorema deTales, es decir,
8
24
=
𝑥
15
. Luego resolvemos la proporción; esto es:
24 ∗ 𝑥 = 8 ∗ 5
𝑥 =
8 ∗ 5
24
𝑥 = 5
2) En la figura L1 // L2 // L3 , T y S son
transversales, calcula x y el trazo CD
Resolución:
Formamos la proporción
3
2
=
𝑥+4
𝑥+1
; resolvemos la
proporción de la siguiente manera:
3 ∗ 𝑥 + 1 = 2 ∗ (𝑥 + 4)
3𝑥 + 3 = 2𝑥 + 8
3𝑥 − 2𝑥 = 8 − 3
𝑥 = 5
Luego como;
CD=𝑥 + 4 entonces CD=5 + 4 = 9

6. APLICACIONES DEL TEOREMA DE THALES EN LA VIDA REAL
Sirve para calcular alturas de edificios teniendo referencias de otros elementos que si que nos es fácil medir,
como por ejemplo un árbol y ayudándonos en los rayos del sol, las proyecciones de sobra.
Escribimos la proporción:
6
5
=
270
ℎ
(Siendo h la altura del edificio)
Resolvemos la proporción:
6 × 𝑥 = 270 × 5
𝑥 =
1350
6
𝑥 = 225