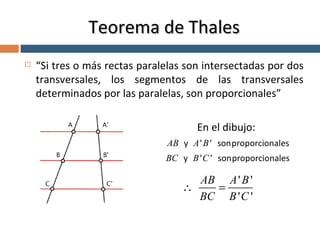
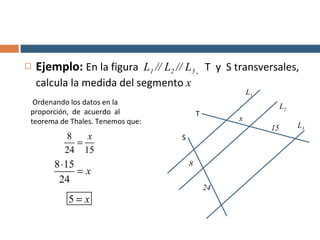
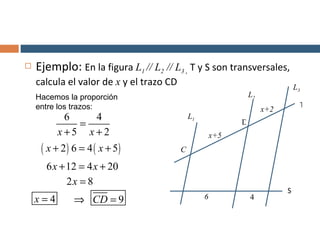
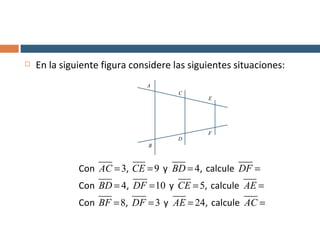
Este documento explica el teorema de Thales, que establece que si tres o más rectas paralelas son cortadas por dos transversales, los segmentos de las transversales determinados por las paralelas son proporcionales. Proporciona un ejemplo numérico para ilustrar cómo aplicar el teorema para calcular un segmento desconocido. Finalmente, propone algunos ejercicios para que el lector aplique el teorema.

1. TEOREMA DE THALES Profesor Practicante: Ignacio Espinoza Braz Comunidad Educativa “San Marcos” Subsector de Matemática Arica

2. Razones y Proporciones Razón: Es el Cuociente entre 2 cantidades. En donde: El numerador es el “antecedente” El denominador es el “consecuente” Ejemplo: La razón entre 36 y 12 es:

3. Proporción: Es una igualdad entre 2 razones. Ejemplo: a y d de denominan extremos b y c son medios

4. Teorema fundamental de las Proporciones En toda proporción se verifica que el producto de los medios es igual al productos de los extremos, es decir:

5. Teorema de Thales “ Si tres o más rectas paralelas son intersectadas por dos transversales, los segmentos de las transversales determinados por las paralelas, son proporcionales” En el dibujo:

6. Ejemplo: En la figura L 1 // L 2 // L 3 , T y S transversales, calcula la medida del segmento x Ordenando los datos en la proporción, de acuerdo al teorema de Thales. Tenemos que: L 1 L 2 L 3 T S 8 24 x 15

7. Ejemplo: E n la figura L 1 // L 2 // L 3 , T y S son transversales, calcula el valor de x y el trazo CD Hacemos la proporción entre los trazos: L 1 L 2 L 3 T S x+5 x+2 6 4 C D

8. Ahora, realiza los siguientes ejercicios aplicando el teorema de Thales . De acuerdo a la figura, encuentre: Ejercicios Propuestos

9. De acuerdo a la figura, encuentre:

10. En la siguiente figura considere las siguientes situaciones: