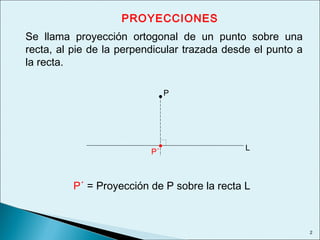
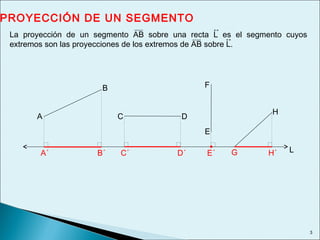
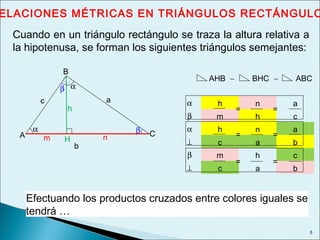
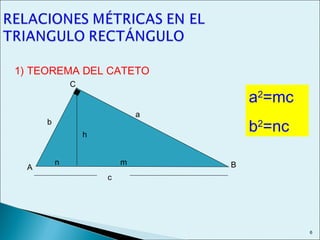
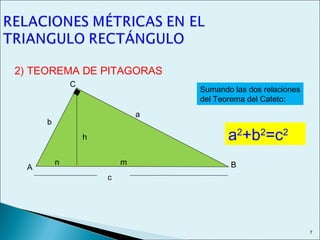
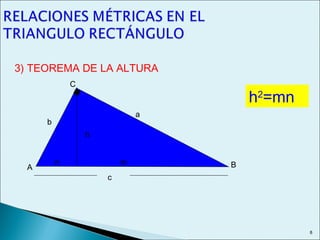
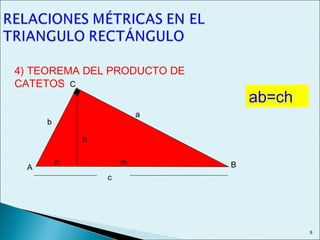
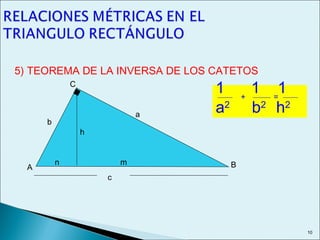
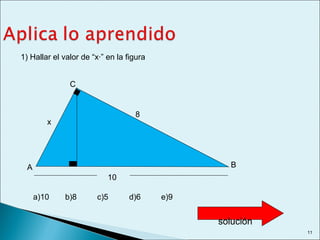
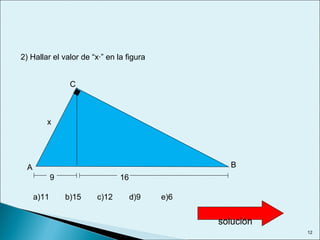
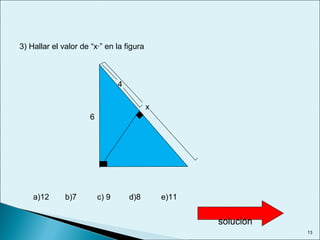
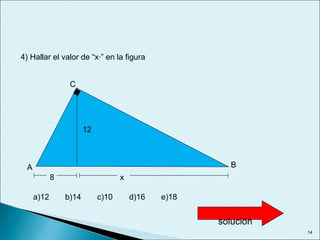
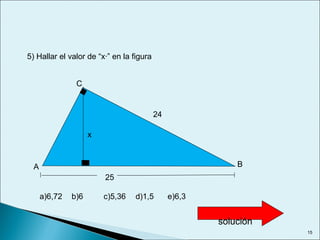
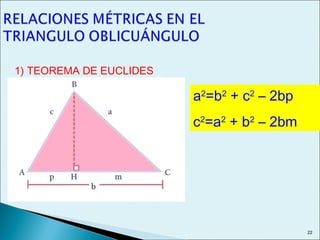
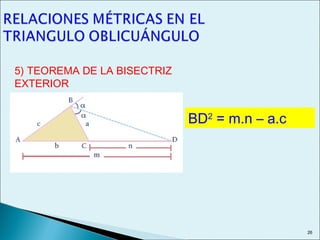
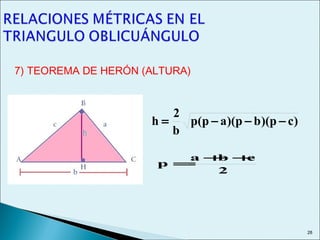
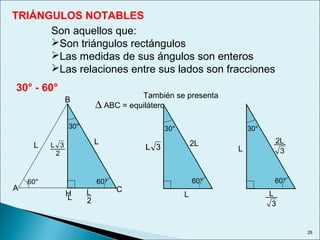
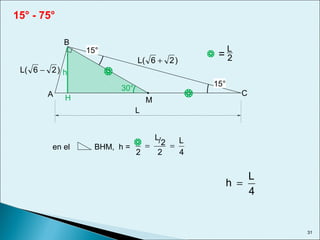
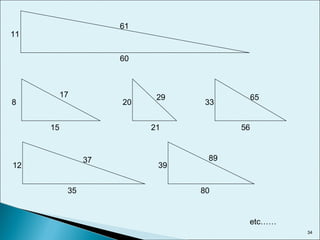
Este documento describe las relaciones métricas en triángulos, incluyendo teoremas como Pitágoras, el cateto y la altura. Explica conceptos como proyecciones ortogonales y resuelve ejercicios numéricos utilizando las fórmulas. También define triángulos notables como el equilátero de 30-60 y triángulos pitagóricos cuyos lados son números enteros en relaciones particulares.