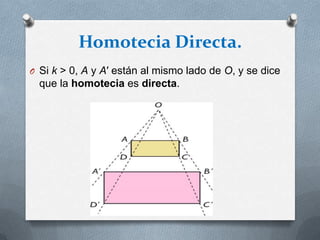
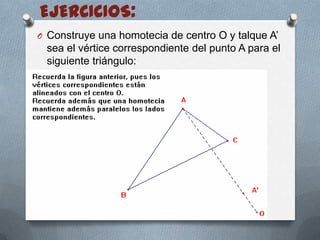
La homotecia es una transformación geométrica que produce figuras de tamaño mayor o menor que la figura original, manteniendo los ángulos pero cambiando las dimensiones de los lados en proporción a una constante de homotecia. Se realiza seleccionando un punto central y trazando segmentos paralelos desde ese punto a los vértices de la figura original.

1. Homotecia.

2. Homotecia. Es la transformación geométrica que no tiene una imagen congruente, ya que a partir de una figura dada se obtienen una o varias figuras en tamaño mayor o menor que la figura dada.Procedimiento.Para obtenerlas se parte de un punto escogido arbitrariamente, al cual se llama centro de homotecia.

3. 2.- Del cual se trazan segmentos de recta, tantos como vértices tenga la figura que se va a transformar. 3.- Se debe considerar otro elemento básico para desarrollar esta transformación, siendo esta una constante, la cual se denomina constante de homotecia que viene a ser la escala en la cual se realiza la reproducción.

4. Tiene las siguientes propiedades:Los ángulos de las figuras por homotecia son iguales ya que tienen la misma medida. Los segmentos con paralelos.Las dimensiones de dos figuras por homotecia son directamente proporciónales; esta proporción es fijada por la constante de homotecia.

5. Homotecia Directa.Si k > 0, A y A′ están al mismo lado de O, y se dice que la homotecia es directa.

6. Homotecia InversaSi k < 0, A y A′ están a distinto lado de O, y se dice que la homotecia es inversa.

7. Como habrás notado, para que el polígono A’B’C’D’E’ conserve la forma y orientación del polígono ABCDE, necesita que los lados correspondientes de ambos polígonos se mantengan paralelos. Pero, al mover el punto O obtienes distintas homotecias en distintas ubicaciones del plano, y al mover el punto E’, obtienes homotecias de distintos tamaños. Esto quiere decir que una homotecia F’ depende del punto O y del tamaño que queremos que tenga la figura F’.

8. La figura A'B'C' se construyó tomando el punto O y trazando paralelas al triángulo ABC.Triángulo OCB es semejante a Triángulo OC'B', entonces: OB'/OB=OC'/OC=B'C'/BCTriángulo OCA es semejante a Triángulo OC'A', entonces: OC'/OC=OA'/OA=C'A'/CALuego, concluimos que: B'C'/BC=C'A'/CALo anterior es válido para todos los lados correspondientes: B'C'/BC=C'A'/CA=B'A'/BA=k (factor de conversión)Por tanto Triángulo ABC es semejante a Triángulo A'B'C'

9. EJERCICIOS:Construye una homotecia de centro O y talque A’ sea el vértice correspondiente del punto A para el siguiente triángulo: