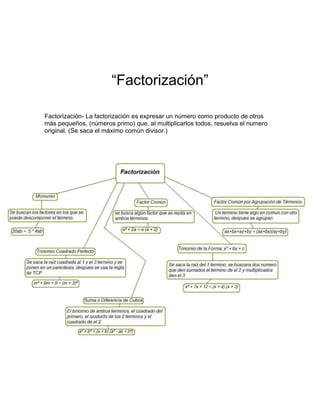
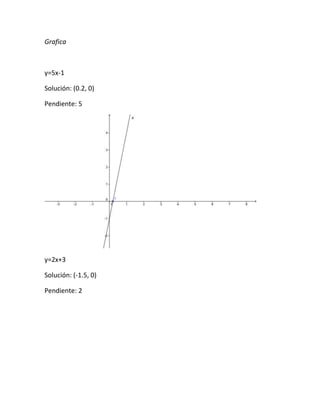
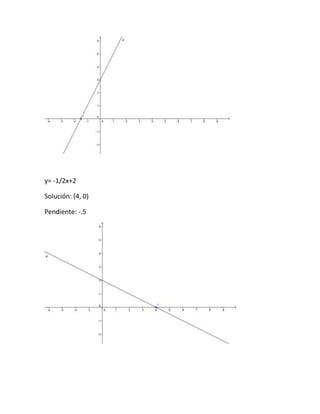
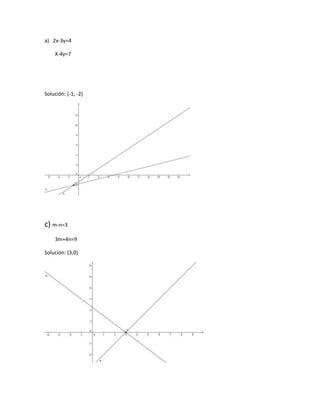
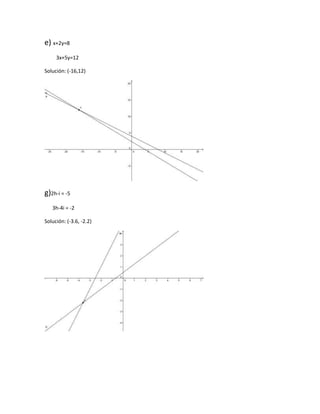
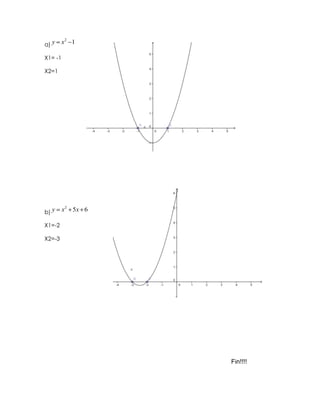
Este documento presenta un resumen de los temas de álgebra vistos en clase, incluyendo suma, resta, multiplicación, división, productos notables, factorización, fracciones algebraicas y ecuaciones lineales. Explica conceptos como términos algebraicos, expresiones algebraicas y exponentes, y provee ejemplos para ilustrar cada operación y concepto cubierto.

1. CEDART <br /> DAVID ALFAROS SIQUEIROS<br />ALGEBRA I <br />“Trabajo final”<br />Jessica Torres Nava<br />“A”

2. Índice

3. Introducción………………………………………………………..

4. Suma………………………………………………………………..

5. Resta………………………………………………………………..

6. Multiplicación……………………………………………………….

7. División………………………………………………………………

8. Productos Notables…………………………………………………

9. Factorización………………………………………………………

10. Fracciones Algebraicas……………………………………………

11. Ecuaciones Lineales………………………………………………

12. Introducción

13. -Conceptos

14. Algebra -- Parte de las matemáticas que estudia la relación entre números y variables para constituir modelos matemáticos y realizar operaciones

15. Usos – Suma, resta, multiplicación, división, productos notables, factorización, fracciones algebraicas y ecuaciones algebraicas.

16. Termino Algebraico – signo, coeficiente, variable y exponente

17. Expresión Algebraica – Monomio, binomio, trinomio y polinomio

18. Exponentes – lineal, cuadrático, cubico o grado (4º, 5º 6º)

19. Este trabajo es un repaso de todo lo que hemos visto en clase, es un forma para que se nos grabe la información de estos temas.

21. SUMA En una pastelería Tres amigos llegaron a comprar panecillos, uno de ellos se llevó tres donas, cuatro conchas y un cochinito, otro llevó dos galletas, cuatro donas y tres cochinitos, y el último de los amigos llevó una concha, cuatro cochinitos y cuatro galletas. <br />DonasXCochinitoq ConchasYGalletasP<br />¿Cuánto pagaron en total?<br />Polinomio lineal<br /> <br /> Polinomio cubico<br />Trinomio cuadrático}<br /> <br /> Trinomio lineal <br /> Trinomio cuadrático<br />Trinomio cubico<br /> <br />RESTA<br />En C&A Julia compró siete pantalones, cuatro blusas y cuatro pares de zapatos, al siguiente día su hermana se llevó cuatro chamarras, dos pares de zapatos, un pantalón y dos blusas. La mamá al fin del mes pagó cinco pantalones, tres blusas, dos chamarras y dos pares de zapatos.<br />¿Cuanto quedó debiendo la mamá?<br />Pantalones XBlusasYZapatosqchamarrasp<br /> <br />Polinomio lineal<br />MULTIPLICACION<br />LEY DE SIGNOS<br />(+) por (+) da (+)(+) por (-) da (-)(-) por (+) da (-) (-) por (-) da (+)<br />PROPIEDAD DISTRIBUTIVA<br />La propiedad distributiva de la multiplicación – Un sumado de dos o mas números multiplicado por un número X es igual a la suma de el producto de cada número por el número X sumado. Ejemplo<br />(b + a) . X = (b . X) + (a . X)<br />LEY DE EXPONENTES<br />Aquellos números o bases que están elevados a una potencia constan de leyes que deben de cumplirse en cada operación matemática, por ejemplo:<br /> Cuando dos números elevados a cierta potencia se están multiplicando, los exponentes se suman; Cuando se dividen, los exponentes se restan; cuando son elevados a otra potencia, los exponentes se multiplican; y cuando aquellos exponentes son encerrados en una raíz, su resultado es un exponente fraccionario.<br />EJEMPLOS:<br /> <br />* Todo número elevado a cero es igual a la unidad: a0= 1* Para multiplicar potencias de la misma base, se suman los exponentes: a5. a 3= a8* Para dividir potencias de la misma base, se restan lo exponentes: a5/ a 3= a2* Para elevar una potencia a otra potencia, se multiplican los exponentes: (a5)3 = a15* Una potencia con exponente negativo será lo mismo que uno partido por la misma potencia con exponente positivo: a- 5= 1 / a5* Una potencia con exponente fraccionario, equivale a una raíz: a3/4= <br />PASOS<br />Los coeficientes se multiplican aplicando la ley de los signos<br />Los exponentes de las mismas literales se suman y se aplican a la ley distributiva<br />Se simplifica sumando términos semejantes; ordenar y clasificar<br />EJEMPLO<br /> Trinomio cuadrado<br />Polinomio de 4° grado<br />Polinomio cubico<br />Polinomio cubico<br />Trinomio de 7° grado<br />Polinomio<br />Polinomio de 4° grado<br />Trinomio cuadrático<br />Polinomio cubico<br />Polinomio de 5° grado<br />1-Un terreno rectangular mide 2x – 4 metros de largo y 5x +3 de ancho ¿Cuál es el modelo matemático que expresa su área?<br />Trinomio cuadratico<br />2-En una tienda se compraron tres diferentes artículos A, B y C. A cuesta 3x por unidad y se compran 5 unidades, B cuesta 4x + 2 por unidad y se compraron 3 unidades y C cuesta x por unidad y se compraron 7 unidades. ¿cuál es el modelo matemático del costo total de la compra?<br />Trinomio <br />División<br />La división es la operación que tiene por objeto repartir un numero en tantas partes iguales<br />Si un espacio rectangular tiene un área de QUOTE y la anchura es de 3x-5 ¿Cuánto mide la base? b=2x+3<br />A= 6 QUOTE --19x+15<br />a= 3x-5<br /> <br />Polinomio entre monomio<br />*Los coeficientes se dividen o se simplifican aplicando la ley de los signos.<br />*Los exponentes de las mismas literales se restan si quedan residuos se indica donde estaba el mayor.<br />Polinomio entre polinomio<br />*Los coeficientes se dividen<br />*si el exponente de adentro es mas chica que la de afuera no se puede dividir<br />Productos notables<br />Binomio al cuadrado<br />*Cuadrado del primero<br />*Multiplicar el primero por el segundo y luego el cuadrado de los dos juntos<br />*Cuadrado del segundo<br />Binomio al cubo<br />*Cubo del primero<br />*Triple producto del cuadrado del primero por el segundo<br />*Triple producto del cuadrado del segundo por el primero<br />*Cubo de el segundo<br />Binomio a la potencia superior<br />*La primera inicia con la potencia indicada <br />*El segundo inicia en cero y aumenta asta la potencia indicada <br />Binomios con termino común<br />*Cuadrado del común<br />*suma o resta de los diferentes por el común<br />*producto de los diferentes<br />Binomios conjugados<br />*Cuadrado del primero<br />*(-) menos cuadrado de el segundo<br />Conclusión de la primera evaluación<br />Suma, resta y multiplicación<br />Suma*Los coeficientes son los que se suman<br />*Signos iguales se suman <br />*Signos diferentes se restan (signo de el mayor)Trinomio lineal<br />*Ordenar y clasificar<br />Resta*Se cambia el signo a todos los términos de la expresión antecedida por (--)<br />*Sumar <br />*Ordenar y clasificar<br />Multiplicación*Los coef. Se multiplican aplicando la ley de los signos <br />*Los exponentes de las mismas literales se suman y se aplica la ley distributiva (Un sumado de dos o mas números multiplicado por un número X es igual a la suma de el producto de cada número por el número X sumado. Ejemplo (b + a) . X = (b . X) + (a . X) )<br />*Se simplifica sumando los términos semejantes <br />*Ordenar y clasificar<br />Conclusión de la segunda evaluación <br />División y productos notables<br />DivicionExisten tres tipos de división<br />Monomio entre monomio

22. Polinomio entre monomio

23. Polinomio entre polinomioPara los dos primeros las reglas son iguales<br />*Los coef. Se dividen o simplifican aplicando la ley de los signos<br />*Los exponentes de las mismas literales se restan si queda residuo se indica donde estaba el mayor<br />*El coef. 1 solo indicara arriba si es lo único que queda<br />Monomio entre monomio Polinomio entre monomio<br /> <br />Polinomio entre polinomio<br />*Ordenar <br />*Si la X de adentro es mas chica que la de afuera no se puede dividir<br />Productos notablesSon 5 problemas (cinco operaciones algebraicas)<br />Binomio al cuadrado, al cubo, a potencia superior, con termino común y binomio conjugados<br /> <br />“Factorización”<br />Factorización- La factorización es expresar un número como producto de otros más pequeños, (números primo) que, al multiplicarlos todos, resuelva el numero original. (Se saca el máximo común divisor.)<br />Resolver<br />La factorización en ecuaciones cuadráticas - Consiste en convertir la ecuación en un producto de binomios, luego se busca el valor de X<br />Conclusión - Aprendimos métodos de factorización y los pusimos en práctica. <br />“Fracciones Algebraicas”<br />Resolver<br />Fracción compleja – Es cuando el numerador o el denominador, o ambos, contienen fracciones. <br /> “Ecuaciones Lineales”<br />La ecuación lineal - Es un planteamiento de igualdad, involucrando una o más variables a la primera potencia, que no contiene productos entre las variables, es una ecuación que involucra solamente sumas y restas de una variable a la primera potencia.<br />Tipos - Ecuación general, Ecuación segmentaria o simétrica, Forma paramétrica o Casos especiales.<br />Formas – Suma y resta o, Igualación.<br /> <br />Grafica<br />y=5x-1<br />Solución: (0.2, 0)<br />Pendiente: 5<br />y=2x+3<br />Solución: (-1.5, 0)<br />Pendiente: 2<br />y= -1/2x+2<br />Solución: (4, 0)<br />Pendiente: -.5<br />a) 2x-3y=4<br /> X-4y=7<br />Solución: (-1, -2)<br />c) m-n=3<br /> 3m+4n=9<br />Solución: (3,0)<br />e) x+2y=8<br /> 3x+5y=12<br />Solución: (-16,12)<br />g)2h-i = -5<br /> 3h-4i = -2<br />Solución: (-3.6, -2.2)<br />Se vendieron boletos para una obra de teatro escolar a $4.00 para adultos y $1.50 para niños. Si se vendieron 1000 boletos recaudando $3,500. ¿Cuántos boletos de cada tipo se vendieron?<br />Adultos: 800 boletos.<br />Niños: 200 boletos.<br />Si se mezcla una aleación que tiene 30% de Ag con otra que contiene 55 % del mismo metal para obtener 800 kg de aleación al 40%. ¿Qué cantidad de cada una debe emplearse?<br />x+y= 800<br />.3x+.55y= 800(.4)= 320<br />480 kg de Ag al 30%<br />320 kg de Ag al 55%<br />“Ecuaciones de 2º Grado”<br />Una ecuación cuadrática representa una parábola vertical donde la solución son los puntos de intersección con X<br />Los números imaginarios son aquellos a los que no podemos sacarle raíz cuadrada por ser negativo, pero podemos agregarle un i (imaginario) para que a esos números negativos se les llame números imaginarios<br />a)<br />X1= -1<br />X2=1<br />b)<br />X1=-2<br />X2=-3 <br />Fin!!!!<br />