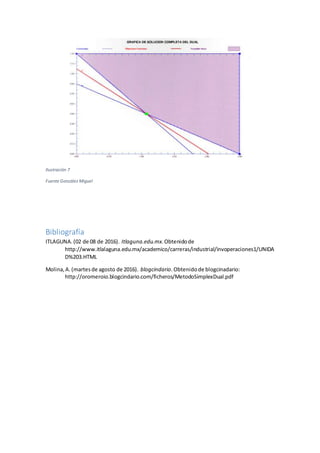
El documento presenta información sobre la dualidad en el método simplex. Explica que cada problema de programación lineal tiene un problema dual asociado, y describe cómo obtener el problema dual a partir del problema primal. También define el concepto de dualidad y explica cómo aplicar el método dual-simplex para resolver problemas óptimos pero infactibles, usando un ejemplo numérico para ilustrar el proceso.

1. UNIVERSIDAD TÉCNICA DE AMBATO
INVESTIGACIÓN OPERATIVA I
TRABAJO FINAL
DUALIDAD EN MÉTODO SIMPLEX
JOHANNA ALTAMIRANO
5º “A”
CONTEXTUALIZACIÓN
(Molina, 2016) Menciona: “Cada problema de programación lineal tiene un segundo
problema asociado con él. Uno se denomina primal y el otro dual. Los 2 poseen
propiedades muy relacionadas, de tal manera que la solución óptima a un problema
proporciona información completa sobre la solución óptima para el otro.”
(ITLAGUNA, 2016) Menciona: “El problema dual se puede obtener a partir del problema
primal y viceversa de la siguiente manera:
1. Cada restricción de un problema corresponde a una variable en el otro.
2. Los elementos del lado derecho de las restricciones en un problema son iguales a los
coeficientes respectivos de la función objetivo en el otro.
3. Un problema busca maximizar y el otro minimizar.
4. El problema de maximización tiene restricciones que y el problema de minimización
tiene restricciones que.
5. Las variables en ambos casos son no negativas.”
CONCEPTO
El método dual-símplex, utilizado hasta ahora para resolver modelos de programación lineal en
su forma estándar, ha demostrado ser una eficiente herramienta en apoyo a la toma de
decisiones basadas en resultados cuantitativos.
Sin embargo, los problemas o casos a resolver no siempre se presentan de tal manera que puedan
expresarse en la forma estándar y resolverse por el método dual-símplex, por lo que es necesario
plantear una metodología para resolver estos casos. Se tiene un método aprovechando uno de los
resultados del desarrollo de la programación lineal, el concepto de dualidad plantea que, asociado
a todo problema de programación lineal, existe otro problema lineal llamado dual. En este capítulo
se desarrolla la teoría y aplicación del método dual-símplex en la resolución de problemas y casos
prácticos.

2. APLICACIÓN
Este método es aplicable a problemas óptimos pero infactibles. En este caso, las
restricciones se expresan en forma canónica (restricciones).
La función objetivo puede estar en la forma de maximización o de minimización.
(Molina, 2016) Nos dice. “Después de agregar variables de holgura y de poner el
problema en la tabla, si algún elemento de la parte derecha es negativo y la condición de
optimidad está satisfecha, el problema puede resolverse por método simplex. Note que
un elemento negativo en el lado derecho significa que el problema comienza óptimo pero
infactible como lo que se requiere en el método dual simplex. En la iteración donde la
solución básica llega a ser factible esta será la solución óptima del problema.”
CONDICIONES
CONDICION DE FACTIBILIDAD
La variable que sale es la variable básica que tiene el valor más negativo porque los empates se
rompen arbitrariamente si todas las variables básicas son no negativas, el proceso termina y esta
última tabla es la solución óptima factible).
La variable que entra se elige de entre la no básica como sigue. Tome los cocientes de los
coeficientes de la función objetivo entre los coeficientes que corresponda a la ecuación asociada
a la variable que sale.
Se debe ignorar los cocientes asociados a denominadores positivos o cero.
La variable que entra es aquella con el cociente más pequeño si el problema es de minimizar o el
valor absoluto más pequeño si el problema es de max.
EJEMPLO

3. Un fabricante tienes dos recursos R1 y R2.
Estos recursos pueden usarse para producir dos productos diferentes A y B de acuerdo con la
siguiente regla:
Para producir “A” se emplean 1 unidad de R1 y 4 unidades de R2 para producir B se emplean 1
unidades de R1 y 2 unidades de R2.
El fabricante solo cuenta con 3 unidades de R1 y 6 unidades de R2.
Recibe una ganancia por unidad de A de $3.50 y por unidad de B de $2.50
¿Cuántas unidades de “A” y B debe producir para maximizar sus ganancias?
Tabla de doble entrada para facilitar la construcción de modelo matemático con la información
de referencia.
Tabla re-escrtita multiplicando por 100 (excepto la proporcionalidad) y considerando la
interrelación de los datos del problema.
Ilustración 1
Fuente:González Miguel
Ilustración 2
Fuente:González Miguel

4. MODELO MATEMÁTICO
RESULTANTE
Rotamos la tabla original dándole la vuelta 90º grados en sentido opuesto a las manecillas del
reloj.
Ilustración 3
Fuente:González Miguel
Ilustración 4
Fuente González Miguel

5. Ilustración 5
Fuente González Miguel
Ilustración 6
Fuente González Miguel
MODELO
MATEMÁTICO
RESULTANTE

6. Ilustración 7
Fuente González Miguel
Bibliografía
ITLAGUNA.(02 de 08 de 2016). Itlaguna.edu.mx.Obtenidode
http://www.itlalaguna.edu.mx/academico/carreras/industrial/invoperaciones1/UNIDA
D%203.HTML
Molina,A.(martesde agosto de 2016). blogcindario.Obtenidode blogcinadario:
http://oromeroio.blogcindario.com/ficheros/MetodoSimplexDual.pdf