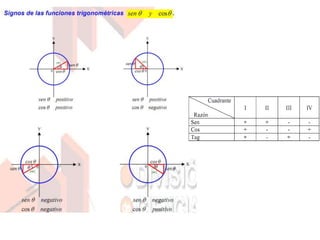
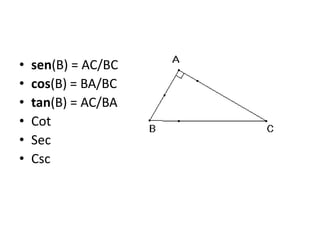
El documento trata sobre la trigonometría. Explica que la trigonometría estudia las razones trigonométricas en los triángulos y cómo resolver triángulos rectángulos y no rectángulos usando el teorema de Pitágoras, funciones trigonométricas, leyes de seno y coseno. También define conceptos como el círculo trigonométrico e identidades trigonométricas.

1. TRIGONOMETRIA
FER VILLALBA

2. Trigonometría
NO OLVIDES QUE SI
TIENES ALGUNA
DUDA, TUS
• La trigonometría es una rama de la PROFESORES
PUEDEN AYUDARTE
matemática, cuyo significado es
"la medición de los triángulos"
• En términos generales, la trigonometría es el
estudio de las razones
trigonométricas: seno, coseno; tangente,
cotangente; secante y cosecante.

3. ¿Cómo se resuelve un triángulo
rectángulo?
Cateto
B Triángulo
Rectángulo y sus
A
partes
Cateto
SE RESUELVE PARA ENCONTRAR SUS LADOS, ÁNGULOS Y SU ÁREA.
Para conocer sus lados se utiliza el TEOREMA DE PITÁGORAS:
C² = A² + B²
Para conocer sus ángulos se emplean las FUNCIONES TRIGONOMETRICAS:
Y para conocer su área se utiliza la FÓRMULA :

4. Datos a tomar
en cuenta: la
suma de los
tres ángulos
de cualquier
triangulo son
180 grados
http://www.youtube.com/watch?v=oK9Ock1w
YfM
Link para ver una
explicación en video

5. Ley de seno
Este tipo de triángulos los podemos
CUANDO SE UTILIZA resolver utilizando la ley de senos o
•El primer caso: es de dos la ley de cosenos.
ángulos y un lado
•Segundo caso: dos lados La fórmula para la ley de senos es:
y un ángulo opuesto alguno sin  sin  sin 
 
de los lados a b c no hay diferencia si la
sin  sin  sin 
tomas así:   pero no las
a b c
puedes mezclar.
Este es un triángulo ABC el ángulo α se escribe en
el vértice de A, el ángulo β se escribe en el vértice
de B y el ángulo γ se escribe en el vértice de C.
γ Los lados que están opuestos al los vértices ABC y
los escribimos con una letra minúscula abc.
α β
http://www.youtube.com/watch?v=6N87t-3bqAo

6. La ley de cosenos se puede
considerar como una extensión
Ley de coseno del teorema de
Pitágoras aplicable a todos los
triángulos
La ley de los Coseno es una expresión que te permite conocer
un lado de un triángulo cualquiera, si conoces los otros dos
y el ángulo opuesto al lado que quieres conocer.
Resolver un triángulo significa obtener el valor de la longitud de sus tres lados y
la medida de sus tres ángulos internos

7. Para resolver triángulos que nos son rectángulos se utiliza la ley de
cosenos y/o la ley de senos. Todo dependerá de los valores conocidos.
Ejemplo:
Supongamos que en el triángulo . Encontrar la
longitud del tercer lado.
Solución:
Para calcular el valor del tercer lado, podemos emplear la ley de cosenos:
http://www.ies.co.jp/math/java/trig/yogen1/yogen1.html

8. Círculo trigonométrico
El círculo con centro en el origen de
coordenadas cuyo radio tenga por medida la
unidad de longitud, se llamará, círculo
trigonométrico.

10. Identidades trigonométricas
• A continuación se expresan las definiciones de las funciones
trigonométricas.
 SENO: Es la razón entre la ordenada y la distancia al origen.
 COSENO: Es la razón entre la abscisa y la distancia al origen.
 TANGENTE: Es la razón entre la ordenada y la abscisa.
 COTANGENTE: Es la razón entre la abscisa y la ordenada.
 SECANTE: Es la razón entre la distancia al origen y la abscisa.
 COSECANTE: Es la razón entre la distancia al origen y la ordenada.

11. • sen(B) = AC/BC
• cos(B) = BA/BC
• tan(B) = AC/BA
• Cot
• Sec
• Csc

12. Función Gráfica
f(x)= senx
f(x)= cos x
f(x)= tan x
f(x) = cot x
f(x)= sec x
f(x)= csc x

13. • http://www.ies.co.jp/math/java/trig/yogen1/yogen1.html
• http://es.wikipedia.org/wiki/Funci%C3%B3n_trigonom%C3%A9trica
• http://www.youtube.com/watch?v=6N87t-3bqAo
• http://recursostic.educacion.es/descartes/web/materiales_didactic
os/triangulos_oblicuangulos_ffsf/Definiciones_y_teoremas.htm
• http://www.wannasol.com/subjects.php?sub=29
• http://cursos.itesm.mx/webapps/portal/frameset.jsp?tab_tab_grou
p_id=_4_1&url=%2Fwebapps%2Fblackboard%2Fexecute%2Flaunch
er%3Ftype%3DCourse%26id%3D_144901_1%26url%3D
• http://dcb.fi-
c.unam.mx/CoordinacionesAcademicas/Matematicas/CapsulasAnte
cedentes/circulo_trig.pdf
• http://www.matebrunca.com/Contenidos/Matematica/Trigonomet
ria/circulo-trigono.pdf