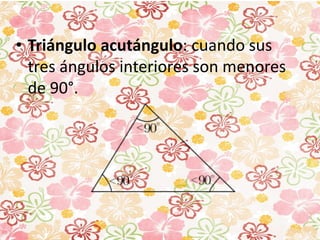
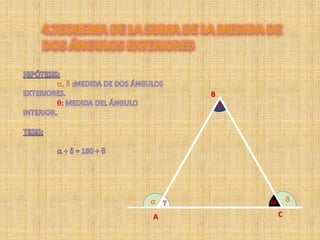
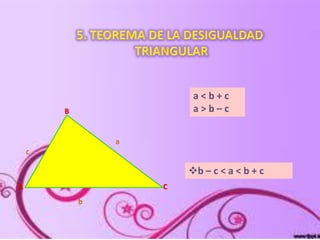
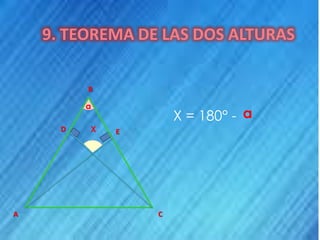
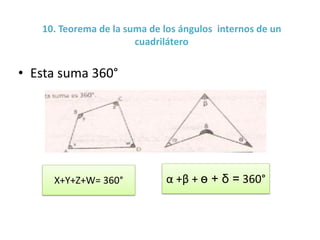
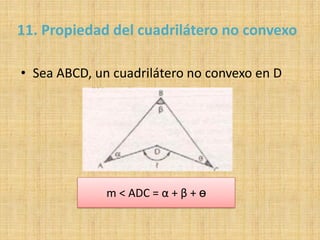
Este documento describe las propiedades de los triángulos y cuadriláteros. Explica que el perímetro de un triángulo es la suma de la longitud de sus tres lados y que la suma de los ángulos internos de un triángulo es igual a 180 grados. También define los diferentes tipos de triángulos basados en la longitud de sus lados o amplitud de sus ángulos internos, como isósceles, equilátero y escaleno.

1. TRIANGULOS

3. A
B
C






4. A
B
C
b
c a
El perímetro de un triángulo es la suma de las
longitudes de sus tres lados y se le representa por
2P.
Perímetro=2P= a + b + c
 a + b + c
El semiperímetro , se representa por P.
Semiperímetro = Perímetro
2
 P= a + b + c
2

5. Propiedades de los
triángulos:
1 Un lado de un triángulo es
menor que la suma de los otros
dos y mayor que su diferencia.
2 La suma de los ángulos
interiores de un triángulo es igual
a 180°.
3 El valor de un ángulo exterior es
igual a la suma de los dos
interiores no adyacentes.

7. Por las longitudes de sus lados
• Triángulo isósceles : si tiene dos lados
de la misma longitud. Los ángulos que se
oponen a estos lados tienen la misma
medida

8. • Triángulo equilátero, cuando los tres lados
del triángulo son del mismo tamaño

9. • Triángulo escaleno , si todos sus
lados tienen longitudes diferentes.

10. Por la amplitud de sus ángulos
• Triángulo rectángulo: si tiene un ángulo
interior recto (90°). A los dos lados que
conforman el ángulo recto se les
denomina catetos y al otro lado hipotenusa.

11. • Triángulo obtusángulo: si uno de sus
ángulos interiores es obtuso (mayor de
90°); los otros dos son agudos (menores
de 90°).

12. • Triángulo acutángulo: cuando sus
tres ángulos interiores son menores
de 90°.

13. A
B
CY Z
X

14. B
A
C
x
y

15. A
B
C
HIPÓTESIS:
, , : medidas de los ángulos
exteriores.
, , : medida de los ángulos
interiores.
TESIS:
 +  + =360°






16. A
B
C

 



17. A
B
C
a < b + c
a > b – c
b – c < a < b + c

18. 


A
B
C
X = 90° +
2


X


19. X
a
A
B
C
E
X = 90 -
2
a

20. 8. TEOREMA DE UNA BISECTRIZ INTERIOR Y
UNA BISECTRIZ EXTERIOR
aX
A
B
C
E
X=
2
aX=
2

21. X
a
A
B
C
ED
9. TEOREMA DE LAS DOS ALTURAS
X = 180° - a

22. 10. Teorema de la suma de los ángulos internos de un
cuadrilátero
• Esta suma 360°
X+Y+Z+W= 360° α +β + ө + δ = 360°

23. 11. Propiedad del cuadrilátero no convexo
• Sea ABCD, un cuadrilátero no convexo en D
m < ADC = α + β + ө