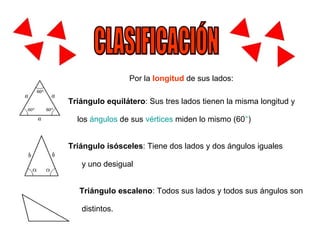
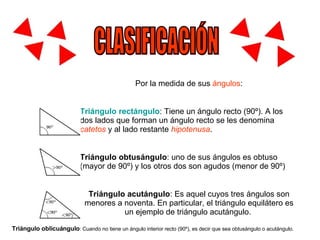
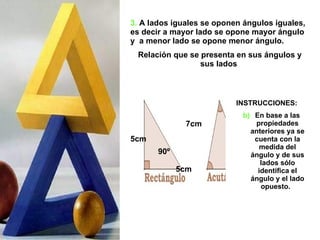
El documento presenta información sobre triángulos, incluyendo sus definiciones, clasificaciones y propiedades. Define un triángulo como una figura plana con tres lados y tres vértices. Explica cómo se clasifican los triángulos por la longitud de sus lados (equilátero, isósceles, escaleno) y por la medida de sus ángulos (rectángulo, obtusángulo, acutángulo, oblicuángulo). También enumera cinco propiedades de los triángulos como la suma de sus ángulos intern

1. ESCUELA NORMAL SUPERIOR PROFESOR MOISÉS SÁENZ GARZA MATEMÁTICAS 4TO. SEMESTRE MATERIA: FIGURAS Y CUERPOS GEOMÉTRICOS MAESTRA: LUZ PATRICIA ROJAS MIRANDA ALUMNOS: FELICITAS RUIZ MUÑIZ MARIO HUMBERTO LÓPEZ RANGEL Monterrey, Nuevo León a; junio de 2007

2. D TEMA 12 ESTUDIO BLOQUE 1 FIGUAS EN EL PLANO CONTENIDOS : Características del triángulo PROPÓSITOS: Inferir propiedades y características del triángulo mediante un estudio detallado. HABILIDADES: Observar, medir e inferir

3. TRIÁNGULO Es un tipo de polígono (o figura plana y cerrada) con el menor número de lados ( tres lados ) es decir, una porción de plano limitada por tres segmentos unidos, dos a dos, por sus extremos. Los tres segmentos que limitan el triángulo se denominan lados , y los extremos de los lados, vértices . En un triángulo se consideran dos tipos de ángulos : interior (formado por dos lados) y exterior (formado por un lado y la prolongación de otro).

4. CLASIFICACIÓN Por la longitud de sus lados: Triángulo equilátero : Sus tres lados tienen la misma longitud y los ángulos de sus vértices miden lo mismo (60 ° ) Triángulo isósceles : Tiene dos lados y dos ángulos iguales y uno desigual Triángulo escaleno : Todos sus lados y todos sus ángulos son distintos.

5. CLASIFICACIÓN Por la medida de sus ángulos : Triángulo rectángulo : Tiene un ángulo recto (90º). A los dos lados que forman un ángulo recto se les denomina catetos y al lado restante hipotenusa . Triángulo obtusángulo : uno de sus ángulos es obtuso (mayor de 90º) y los otros dos son agudos (menor de 90º) Triángulo acutángulo : Es aquel cuyos tres ángulos son menores a noventa. En particular, el triángulo equilátero es un ejemplo de triángulo acutángulo. Triángulo oblicuángulo : Cuando no tiene un ángulo interior recto (90º), es decir que sea obtusángulo o acutángulo.

6. 1 2 3 4 5 6 PROPIEDADES La suma de los ángulos internos suman 180°. INSTRUCCIONES: Medir los ángulos internos de cada triángulo Toma el triángulo, observa e identifica su base. En el caso del triángulo rectángulo se tomará como base la hipotenusa. Posteriormente se volteará el triángulo del lado sin ángulos y se dispondrá a doblar. Nota: Primero doblar vértice superior hacia la base, después los lados para facilitar el dobles.

7. 1 2 3 4 5 6 PROPIEDADES

8. 2. La suma de dos de sus lados debe ser mayor que el tercero a + b > c a + c > b b + c > a La resta de dos de sus lados debe ser menor que el tercero. a – b < c a – c < b b – c < a INSTRUCCIONES: Con el mismo triángulo con el que se esta trabajando medir sus lados. Posteriormente especificar como lado a, b, c. Ahora sustituye su valor con lo antes descrito.

9. 3. A lados iguales se oponen ángulos iguales, es decir a mayor lado se opone mayor ángulo y a menor lado se opone menor ángulo. Relación que se presenta en sus ángulos y sus lados INSTRUCCIONES: En base a las propiedades anteriores ya se cuenta con la medida del ángulo y de sus lados sólo identifica el ángulo y el lado opuesto. 90º 7cm 5cm 5cm

10. 4. Un ángulo exterior es igual a la suma de los dos ángulos interiores no adyacentes. INSTRUCCIONES: Se toma el triángulo existente y se traza uno igual en la hoja de máquina o bien puede pegarse en la hoja para que este no sea trazado. Prolongar cada uno de los lados del triángulo.(encontraremos en cada una de las vértices un ángulo suplementario) Posteriormente inferir cual es la medida del ángulo exterior faltante Teniendo la medida del ángulo exterior sumar los ángulos interiores no adyacentes al ángulo exterior. 180º 105º 30º 75º

11. 5. película