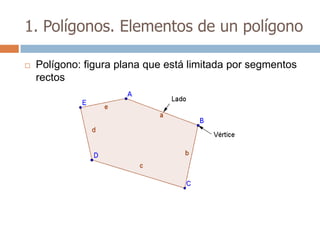
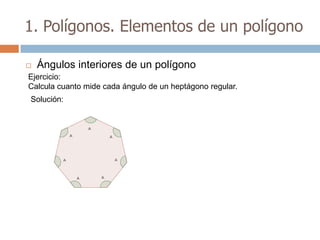
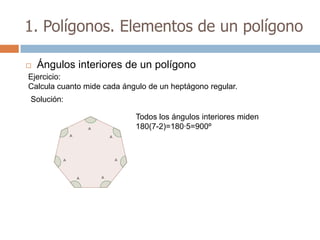
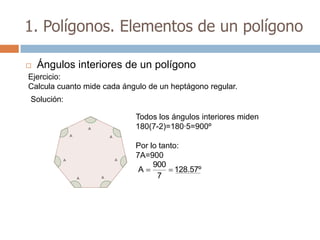
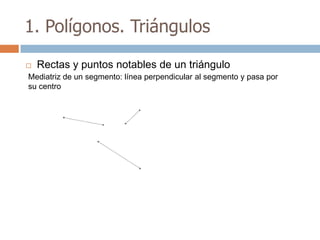
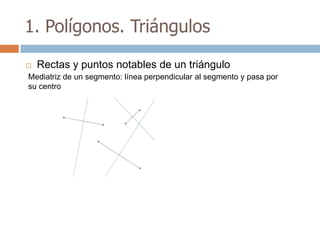
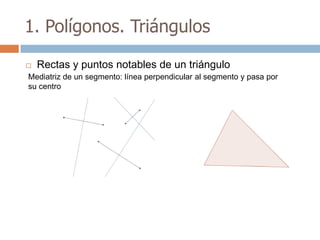
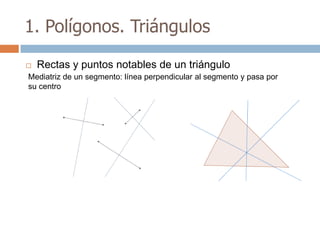
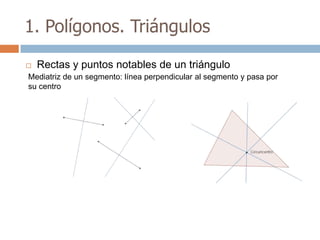
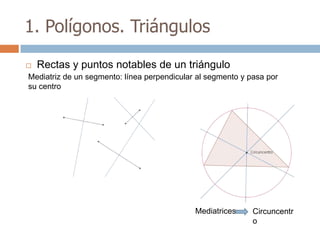
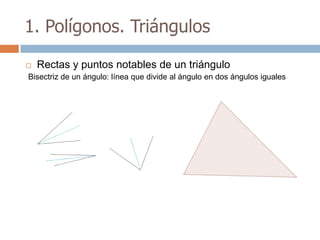
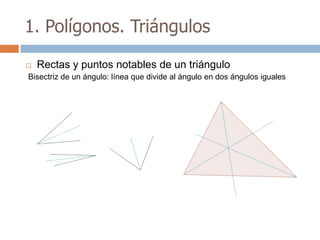
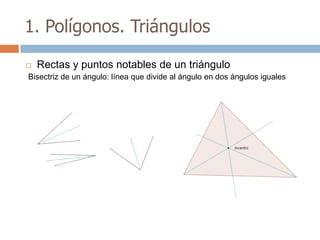
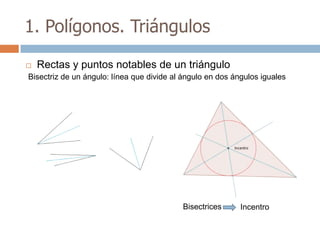
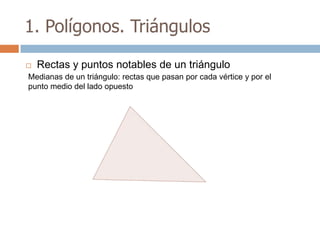
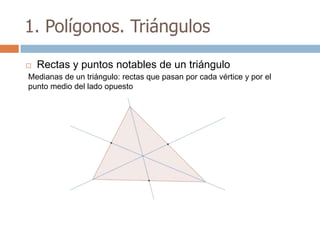
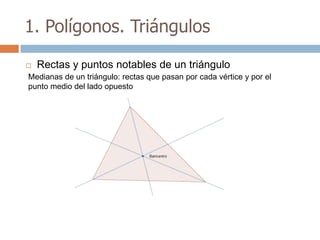
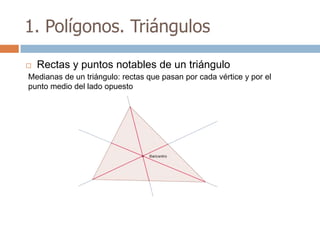
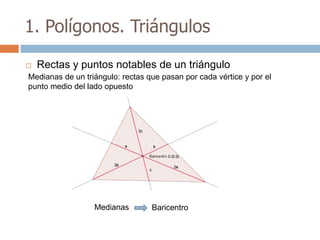
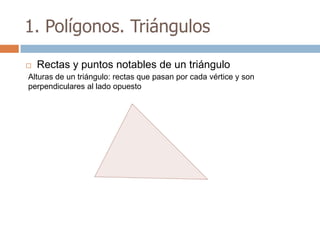
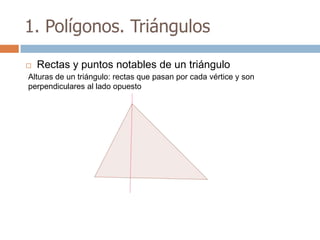
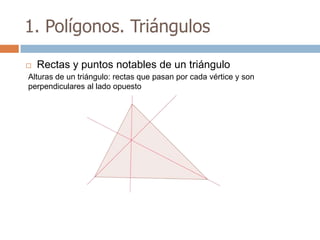
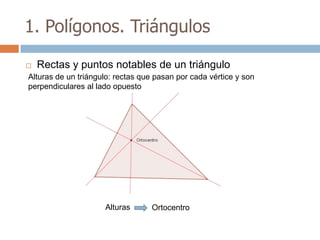
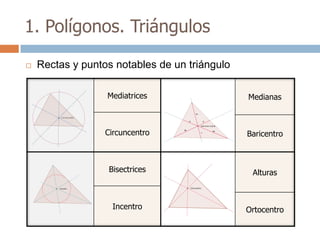
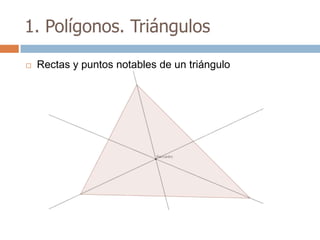
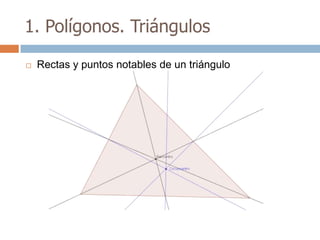
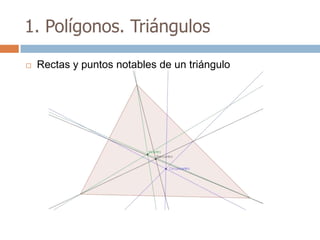
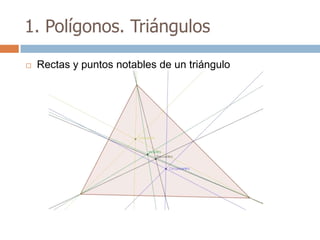
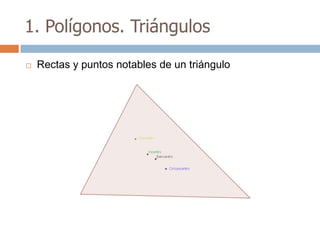
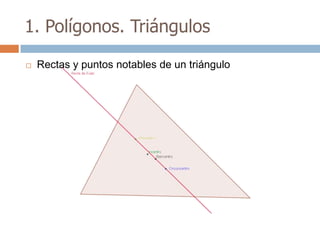
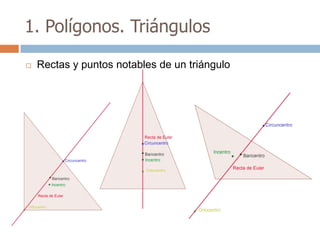
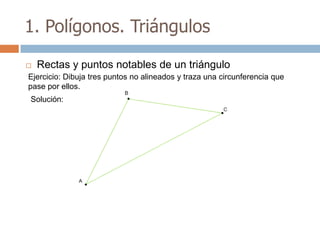
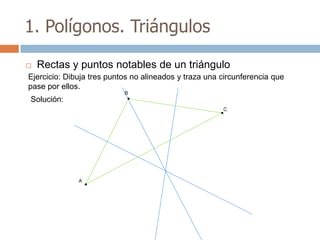
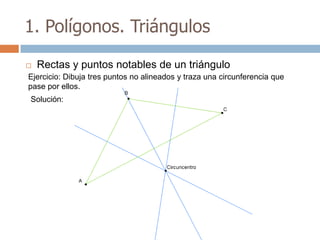
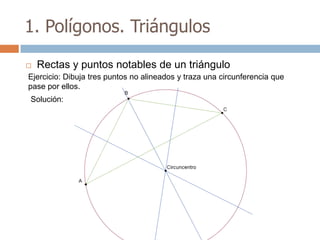
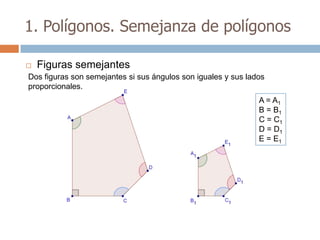
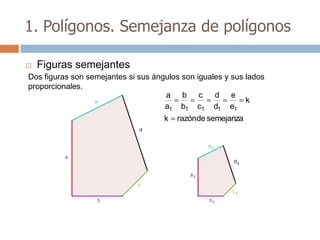
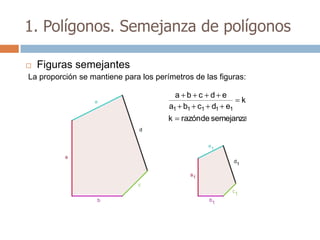
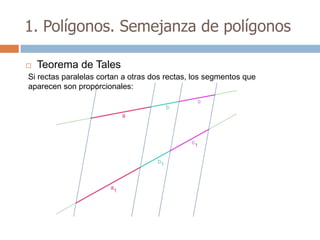
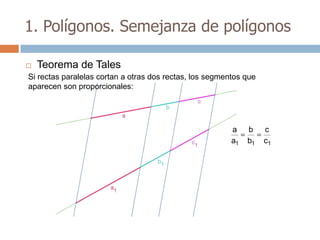
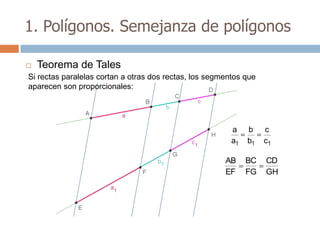
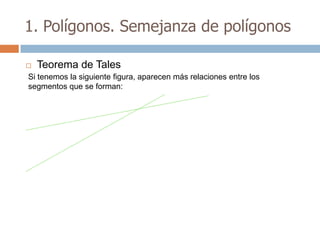
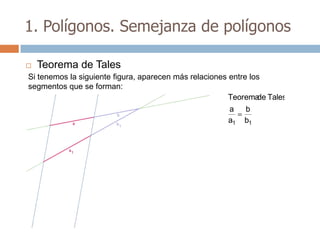
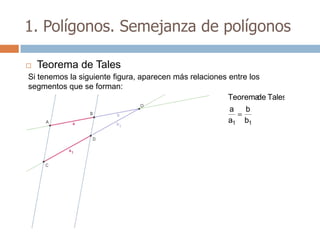
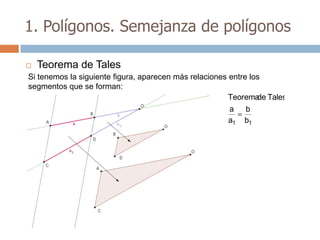
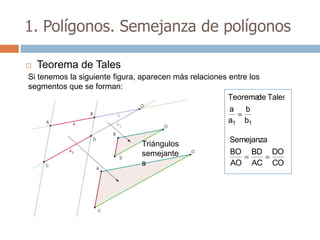
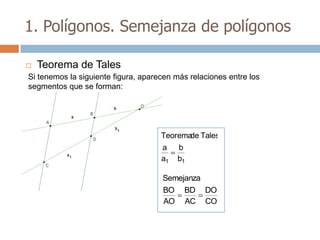
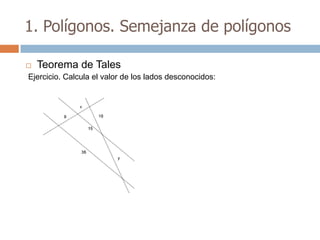
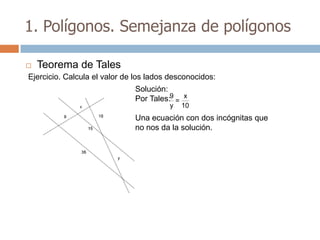
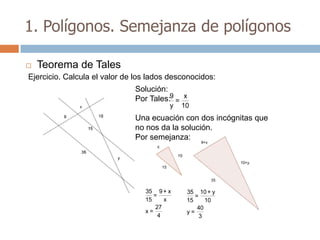
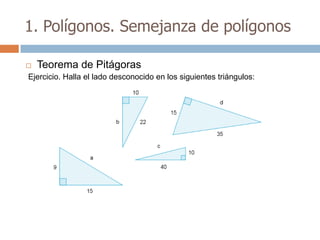
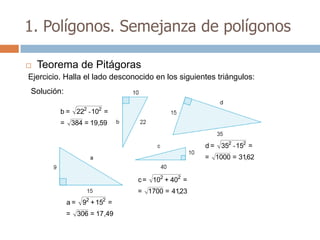
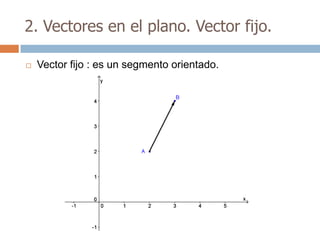
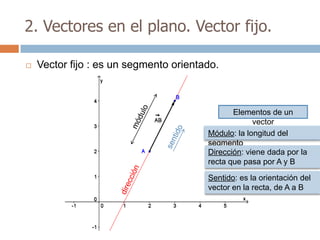
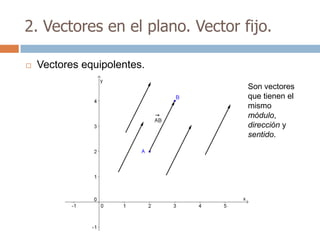
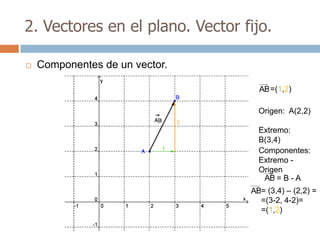
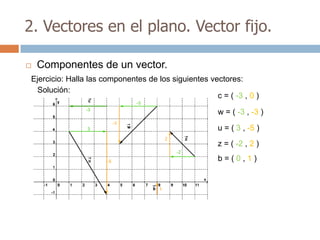
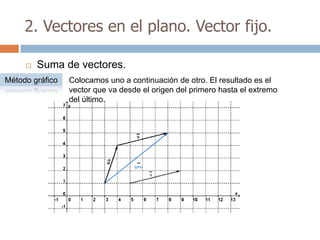
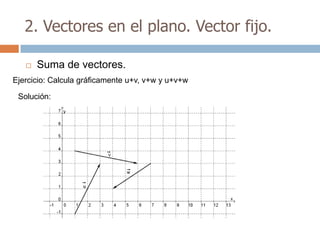
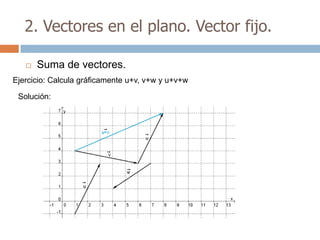
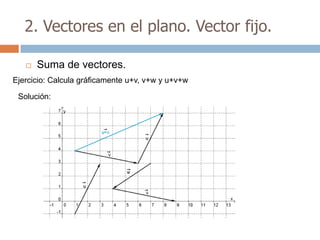
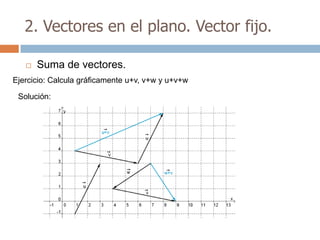
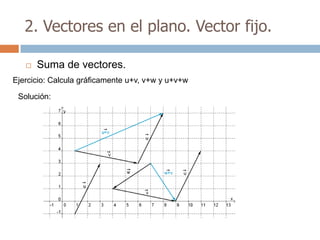
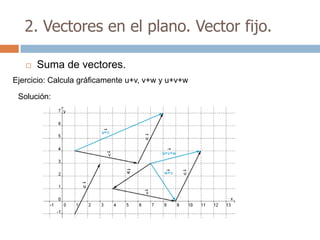
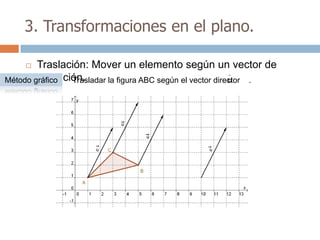
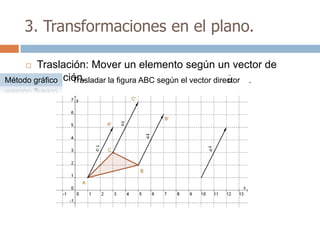
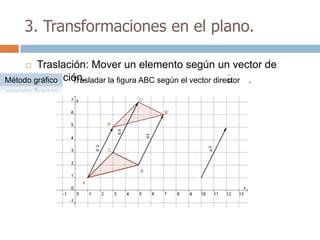
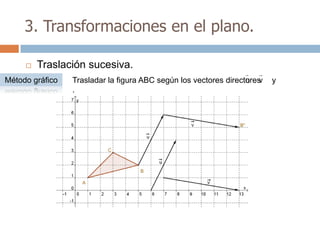
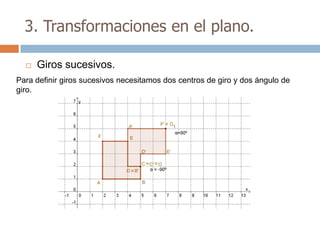
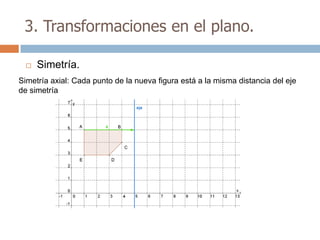
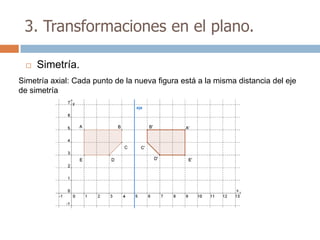
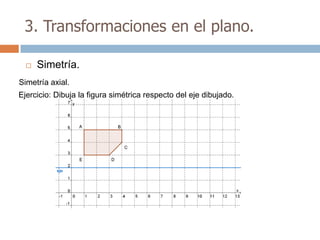
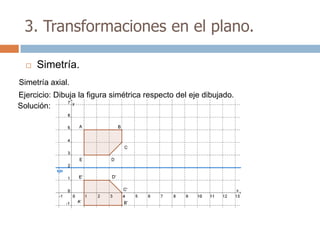
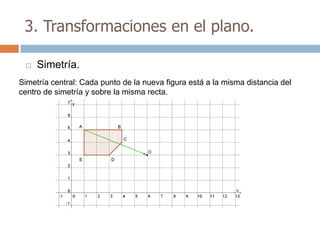
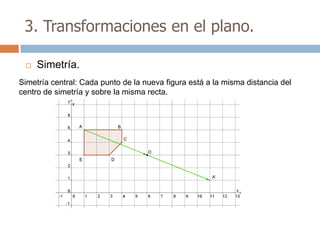
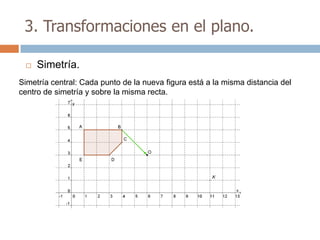
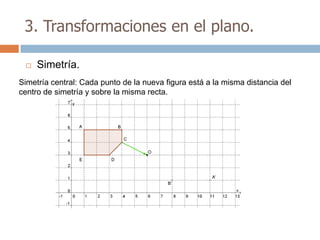
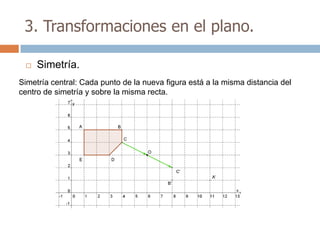
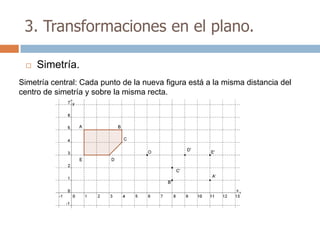
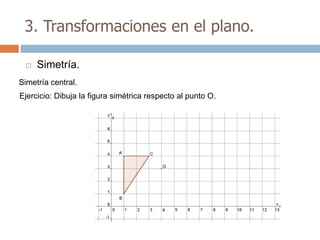
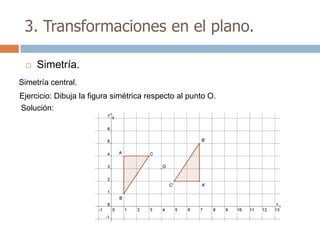
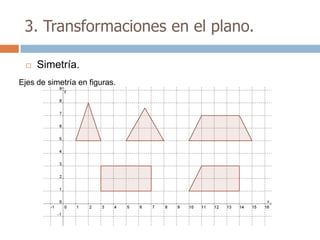
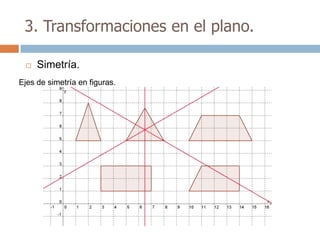
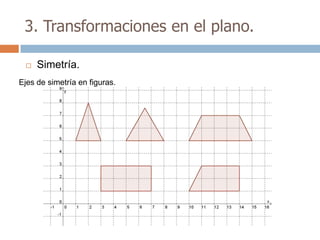
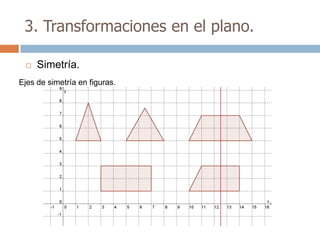
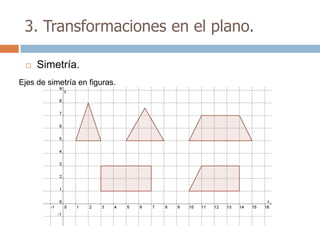
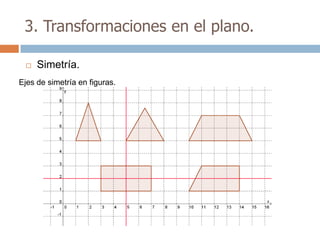
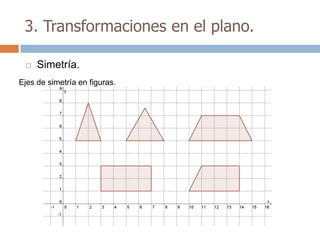
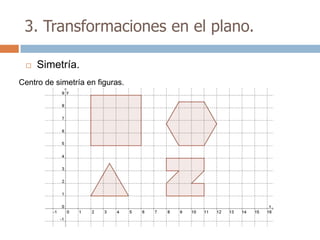
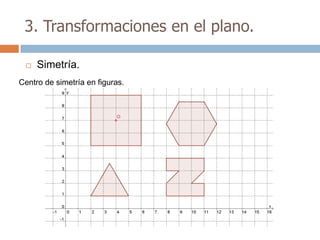
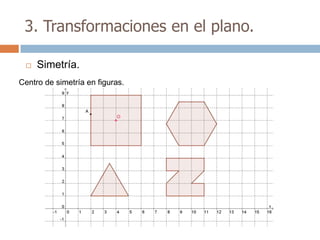
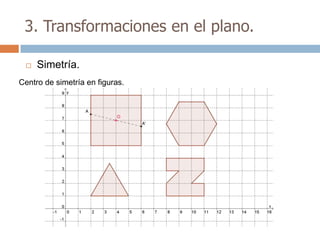
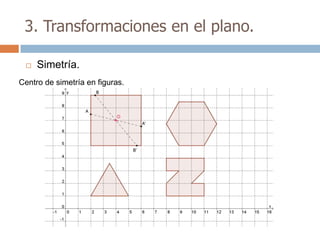
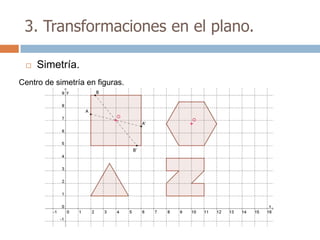
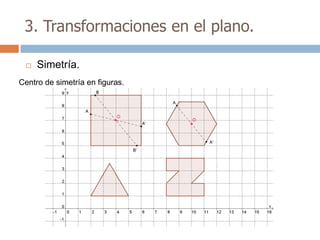
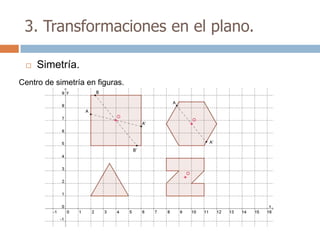
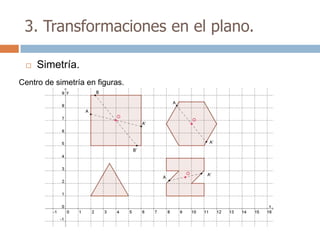
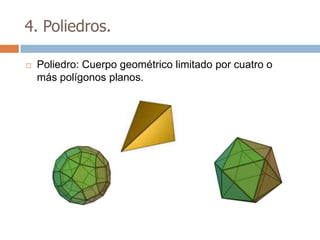
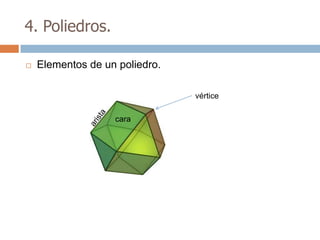
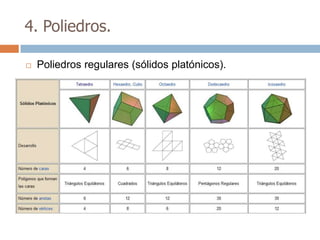
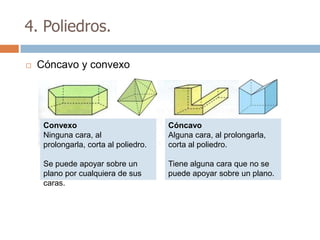
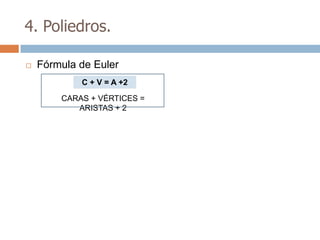
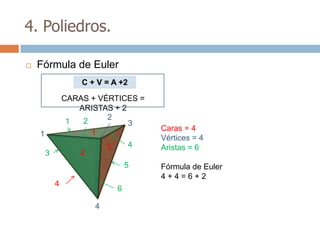
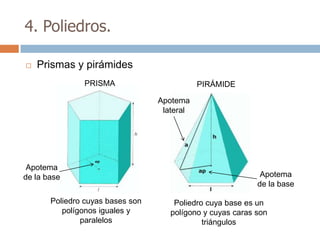
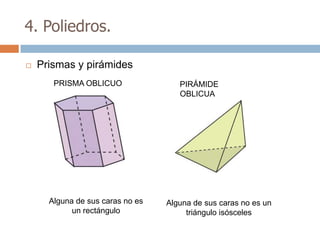
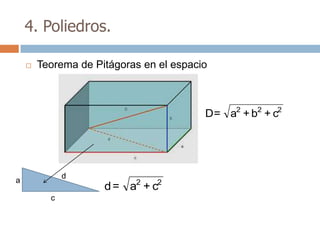
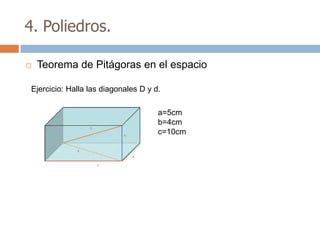
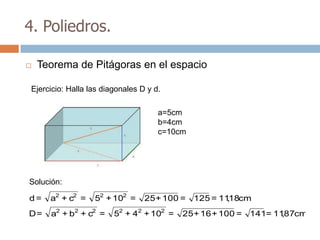
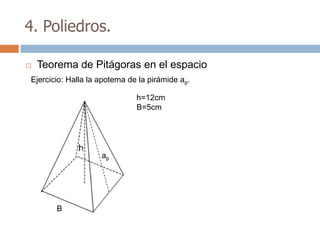
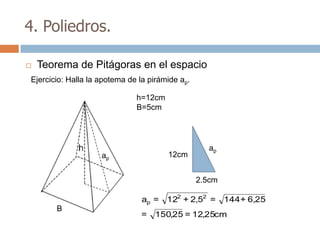
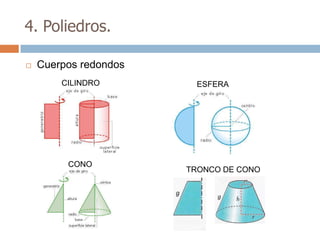
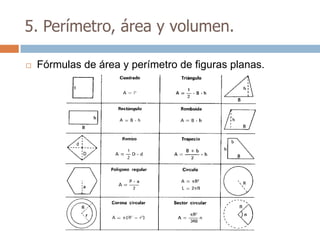
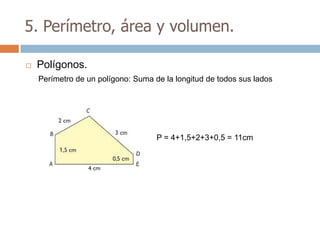
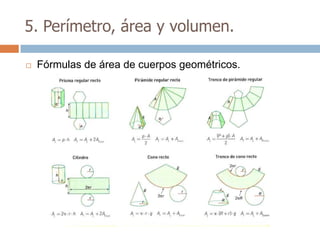
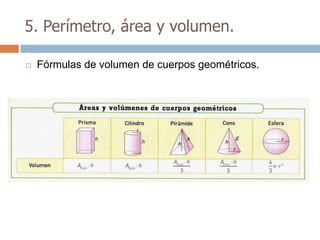
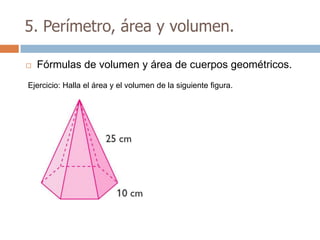
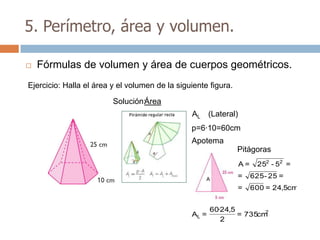
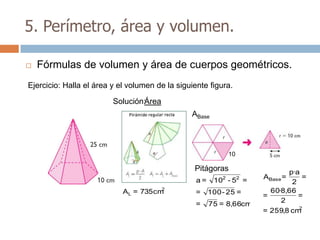
Este documento trata sobre geometría y contiene información sobre polígonos, vectores, transformaciones y poliedros. En la sección de polígonos se define qué es un polígono y sus elementos, y se explican conceptos como la suma de los ángulos interiores, bisectrices, medianas y más. También incluye ejemplos y ejercicios resueltos sobre triángulos y semejanza. Finalmente, presenta el teorema de Tales sobre la proporcionalidad de segmentos cortados por rectas paralelas.

1. TEMA 7 - GEOMETRÍA
1. Polígonos
2. Vectores en el plano
3. Transformaciones en el plano
4. Poliedros
5. Perímetro, área y volumen
ÍNDICE

2. 1. Polígonos. Elementos de un polígono
 Polígono: figura plana que está limitada por segmentos
rectos

3. 1. Polígonos. Elementos de un polígono
 Ángulos interiores de un polígono
La suma de los ángulos interiores de un polígono de n lados es 180º·(n-
2)

4. 1. Polígonos. Elementos de un polígono
 Ángulos interiores de un polígono
La suma de los ángulos interiores de un polígono de n lados es 180º·(n-
2) POLIGONO LADOS SUMA DE TODOS LOS ANGULOS
INTERIORES
3 A+B+C = 180·(3-2) = 180·1 = 180º
4 A+B+C+D = 180·(4-2) = 180·2 = 360º
5 A+B+C+D+E = 180·(5-2) = 180·3 = 540º
6 A+B+C+D+E+F =180·(6-2) = 180·4 = 720º

5. 1. Polígonos. Elementos de un polígono
 Ángulos interiores de un polígono
Ejercicio:
Calcula el valor del ángulo A.

6. 1. Polígonos. Elementos de un polígono
 Ángulos interiores de un polígono
Ejercicio:
Calcula el valor del ángulo A.
Solución:
La suma de todos los ángulos es
180(5-2)=180·3=540º

7. 1. Polígonos. Elementos de un polígono
 Ángulos interiores de un polígono
Ejercicio:
Calcula el valor del ángulo A.
Solución:
La suma de todos los ángulos es
180(5-2)=180·3=540º
Por lo tanto
90+135+90+117+A = 540
432+A=540
A=540-432
A=108º

8. 1. Polígonos. Elementos de un polígono
 Ángulos interiores de un polígono
Ejercicio:
Calcula cuanto mide cada ángulo de un heptágono regular.

9. 1. Polígonos. Elementos de un polígono
 Ángulos interiores de un polígono
Ejercicio:
Calcula cuanto mide cada ángulo de un heptágono regular.
Solución:

10. 1. Polígonos. Elementos de un polígono
 Ángulos interiores de un polígono
Ejercicio:
Calcula cuanto mide cada ángulo de un heptágono regular.
Solución:
Todos los ángulos interiores miden
180(7-2)=180·5=900º

11. 1. Polígonos. Elementos de un polígono
 Ángulos interiores de un polígono
Ejercicio:
Calcula cuanto mide cada ángulo de un heptágono regular.
Solución:
Todos los ángulos interiores miden
180(7-2)=180·5=900º
Por lo tanto:
7A=900
900
A 128.57º
7

12. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Mediatriz de un segmento: línea perpendicular al segmento y pasa por
su centro

13. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Mediatriz de un segmento: línea perpendicular al segmento y pasa por
su centro

14. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Mediatriz de un segmento: línea perpendicular al segmento y pasa por
su centro

15. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Mediatriz de un segmento: línea perpendicular al segmento y pasa por
su centro

16. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Mediatriz de un segmento: línea perpendicular al segmento y pasa por
su centro

17. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Mediatriz de un segmento: línea perpendicular al segmento y pasa por
su centro
Mediatrices Circuncentr
o

18. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Bisectriz de un ángulo: línea que divide al ángulo en dos ángulos iguales

19. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Bisectriz de un ángulo: línea que divide al ángulo en dos ángulos iguales

20. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Bisectriz de un ángulo: línea que divide al ángulo en dos ángulos iguales

21. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Bisectriz de un ángulo: línea que divide al ángulo en dos ángulos iguales

22. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Bisectriz de un ángulo: línea que divide al ángulo en dos ángulos iguales

23. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Bisectriz de un ángulo: línea que divide al ángulo en dos ángulos iguales
Bisectrices Incentro

24. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Medianas de un triángulo: rectas que pasan por cada vértice y por el
punto medio del lado opuesto

25. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Medianas de un triángulo: rectas que pasan por cada vértice y por el
punto medio del lado opuesto

26. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Medianas de un triángulo: rectas que pasan por cada vértice y por el
punto medio del lado opuesto

27. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Medianas de un triángulo: rectas que pasan por cada vértice y por el
punto medio del lado opuesto

28. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Medianas de un triángulo: rectas que pasan por cada vértice y por el
punto medio del lado opuesto
Medianas Baricentro

29. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Alturas de un triángulo: rectas que pasan por cada vértice y son
perpendiculares al lado opuesto

30. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Alturas de un triángulo: rectas que pasan por cada vértice y son
perpendiculares al lado opuesto

31. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Alturas de un triángulo: rectas que pasan por cada vértice y son
perpendiculares al lado opuesto

32. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Alturas de un triángulo: rectas que pasan por cada vértice y son
perpendiculares al lado opuesto
Alturas Ortocentro

33. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Mediatrices Medianas
Circuncentro Baricentro
Bisectrices Alturas
Incentro Ortocentro

34. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo

35. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo

36. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo

37. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo

38. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo

39. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo

40. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo

41. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo

42. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Ejercicio: Dibuja tres puntos no alineados y traza una circunferencia que
pase por ellos.

43. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Ejercicio: Dibuja tres puntos no alineados y traza una circunferencia que
pase por ellos.
Solución:

44. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Ejercicio: Dibuja tres puntos no alineados y traza una circunferencia que
pase por ellos.
Solución:

45. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Ejercicio: Dibuja tres puntos no alineados y traza una circunferencia que
pase por ellos.
Solución:

46. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Ejercicio: Dibuja tres puntos no alineados y traza una circunferencia que
pase por ellos.
Solución:

47. 1. Polígonos. Triángulos
 Rectas y puntos notables de un triángulo
Ejercicio: Dibuja tres puntos no alineados y traza una circunferencia que
pase por ellos.
Solución:

48. 1. Polígonos. Semejanza de polígonos
 Figuras semejantes
Dos figuras son semejantes si sus ángulos son iguales y sus lados
proporcionales.

49. 1. Polígonos. Semejanza de polígonos
 Figuras semejantes
Dos figuras son semejantes si sus ángulos son iguales y sus lados
proporcionales.
A = A1
B = B1
C = C1
D = D1
E = E1

50. 1. Polígonos. Semejanza de polígonos
 Figuras semejantes
Dos figuras son semejantes si sus ángulos son iguales y sus lados
proporcionales.
a b c d e
k
a1 b1 c1 d1 e1
k razónde semejanza

51. 1. Polígonos. Semejanza de polígonos
 Figuras semejantes
La proporción se mantiene para los perímetros de las figuras:
a b c d e
k
a1 b1 c1 d1 e1
k razónde semejanza

52. 1. Polígonos. Semejanza de polígonos
 Figuras semejantes
Ejercicio: Averigua qué parejas de figuras son semejantes.

53. 1. Polígonos. Semejanza de polígonos
 Figuras semejantes
Ejercicio: Averigua qué parejas de figuras son semejantes.
Solución:

54. 1. Polígonos. Semejanza de polígonos
 Teorema de Tales
Si rectas paralelas cortan a otras dos rectas, los segmentos que
aparecen son proporcionales:

55. 1. Polígonos. Semejanza de polígonos
 Teorema de Tales
Si rectas paralelas cortan a otras dos rectas, los segmentos que
aparecen son proporcionales:

56. 1. Polígonos. Semejanza de polígonos
 Teorema de Tales
Si rectas paralelas cortan a otras dos rectas, los segmentos que
aparecen son proporcionales:

57. 1. Polígonos. Semejanza de polígonos
 Teorema de Tales
Si rectas paralelas cortan a otras dos rectas, los segmentos que
aparecen son proporcionales:

58. 1. Polígonos. Semejanza de polígonos
 Teorema de Tales
Si rectas paralelas cortan a otras dos rectas, los segmentos que
aparecen son proporcionales:
a b c
a1 b1 c1

59. 1. Polígonos. Semejanza de polígonos
 Teorema de Tales
Si rectas paralelas cortan a otras dos rectas, los segmentos que
aparecen son proporcionales:
a b c
a1 b1 c1
AB BC CD
EF FG GH

60. 1. Polígonos. Semejanza de polígonos
 Teorema de Tales
Si tenemos la siguiente figura, aparecen más relaciones entre los
segmentos que se forman:

61. 1. Polígonos. Semejanza de polígonos
 Teorema de Tales
Si tenemos la siguiente figura, aparecen más relaciones entre los
segmentos que se forman:

62. 1. Polígonos. Semejanza de polígonos
 Teorema de Tales
Si tenemos la siguiente figura, aparecen más relaciones entre los
segmentos que se forman:
Teorema Tales
de
a b
a1 b1

63. 1. Polígonos. Semejanza de polígonos
 Teorema de Tales
Si tenemos la siguiente figura, aparecen más relaciones entre los
segmentos que se forman:
Teorema Tales
de
a b
a1 b1

64. 1. Polígonos. Semejanza de polígonos
 Teorema de Tales
Si tenemos la siguiente figura, aparecen más relaciones entre los
segmentos que se forman:
Teorema Tales
de
a b
a1 b1

65. 1. Polígonos. Semejanza de polígonos
 Teorema de Tales
Si tenemos la siguiente figura, aparecen más relaciones entre los
segmentos que se forman:
Teorema Tales
de
a b
a1 b1
Semejanza
Triángulos
semejante BO BD DO
s AO AC CO

66. 1. Polígonos. Semejanza de polígonos
 Teorema de Tales
Si tenemos la siguiente figura, aparecen más relaciones entre los
segmentos que se forman:
Teorema Tales
de
a b
a1 b1
Semejanza
BO BD DO
AO AC CO

67. 1. Polígonos. Semejanza de polígonos
 Teorema de Tales
Ejercicio. Calcula el valor de los lados desconocidos:

68. 1. Polígonos. Semejanza de polígonos
 Teorema de Tales
Ejercicio. Calcula el valor de los lados desconocidos:
Solución:
Por Tales:9 = x
y 10
Una ecuación con dos incógnitas que
no nos da la solución.

69. 1. Polígonos. Semejanza de polígonos
 Teorema de Tales
Ejercicio. Calcula el valor de los lados desconocidos:
Solución:
Por Tales:9 = x
y 10
Una ecuación con dos incógnitas que
no nos da la solución.
Por semejanza:
35 9 + x 35 10 + y
= =
15 x 15 10
27 40
x= y=
4 3

70. 1. Polígonos. Semejanza de polígonos
 Teorema de Pitágoras
En un triángulo rectángulo, la suma de los cuadrados de los catetos es
igual a la hipotenusa al cuadrado:
a2 b2 c2
a b2 c2
b a2 c 2
c a2 b2

71. 1. Polígonos. Semejanza de polígonos
 Teorema de Pitágoras
Ejercicio. Halla el lado desconocido en los siguientes triángulos:

72. 1. Polígonos. Semejanza de polígonos
 Teorema de Pitágoras
Ejercicio. Halla el lado desconocido en los siguientes triángulos:
Solución:
b = 222 - 102 =
= 384 = 19,59
d = 352 - 152 =
= 1000 = 31,62
c = 102 + 402 =
= 1700 = 41,23
a = 92 + 152 =
= 306 = 17 ,49

73. 1. Polígonos
Elementos de un polígono
Triángulos: rectas y puntos notables
Semejanza de polígonos
2. Vectores en el plano
3. Transformaciones en el plano
4. Poliedros
5. Perímetro, área y volumen
TEMA 7.Geometría.

74. 2. Vectores en el plano. Vector fijo.
 Vector fijo : es un segmento orientado.

75. 2. Vectores en el plano. Vector fijo.
 Vector fijo : es un segmento orientado.
Elementos de un
vector
Módulo: la longitud del
segmento
Dirección: viene dada por la
recta que pasa por A y B
Sentido: es la orientación del
vector en la recta, de A a B

76. 2. Vectores en el plano. Vector fijo.
 Vectores equipolentes.
Son vectores
que tienen el
mismo
módulo,
dirección y
sentido.

77. 2. Vectores en el plano. Vector fijo.
 Componentes de un vector.
AB =(1,2)
Origen: A(2,2)
Extremo:
B(3,4)
Componentes:
Extremo -
Origen
AB = B - A
AB= (3,4) – (2,2) =
=(3-2, 4-2)=
=(1,2)

78. 2. Vectores en el plano. Vector fijo.
 Componentes de un vector.
Ejercicio: Halla las componentes de los siguientes vectores:
Solución:
c = ( -3 , 0 )
w = ( -3 , -3 )
u = ( 3 , -5 )
z = ( -2 , 2 )
b=(0,1)

79. 2. Vectores en el plano. Vector fijo.
 Componentes de un vector.
Ejercicio: Halla las componentes de los vectores AB, AC y BC si
A( 2, 8) , B( -1, 0 ) y C( -3, 7).
Solución:
AB = B-A = (-1, 0)-(2, 8) = (-1-2, 0-8) = (-3, -8)
AC = C-A = (-3, 7)-(2, 8) = (-3-2, 7-8) = (-5, -1)
BC = C-B = (-3, 7)-(-1, 0) = (-3+1, 7-0) = (-2, 7)

80. 2. Vectores en el plano. Vector fijo.
 Suma de vectores.
Método gráfico Colocamos uno a continuación de otro. El resultado es el
vector que va desde el origen del primero hasta el extremo
del último.

81. 2. Vectores en el plano. Vector fijo.
 Suma de vectores.
Método Sumamos las componentes de cada eje:
analítico
Si u=(-3, 5)
v=(2, 9)
u+v=(-3, 5)+(2, 9)=(-3+2, 5+9)=(-1,
14)
u+v=(-1, 14)
Para restar vectores:
Si u=(-3, 5)
v=(2, 9)
u-v=(-3, 5)-(2, 9)=(-3-2, 5-9)=(-5, -4)
u-v=(-5, -4)

82. 2. Vectores en el plano. Vector fijo.
 Suma de vectores.
Ejercicio: Calcula gráficamente u+v, v+w y u+v+w
Solución:

83. 2. Vectores en el plano. Vector fijo.
 Suma de vectores.
Ejercicio: Calcula gráficamente u+v, v+w y u+v+w
Solución:

84. 2. Vectores en el plano. Vector fijo.
 Suma de vectores.
Ejercicio: Calcula gráficamente u+v, v+w y u+v+w
Solución:

85. 2. Vectores en el plano. Vector fijo.
 Suma de vectores.
Ejercicio: Calcula gráficamente u+v, v+w y u+v+w
Solución:

86. 2. Vectores en el plano. Vector fijo.
 Suma de vectores.
Ejercicio: Calcula gráficamente u+v, v+w y u+v+w
Solución:

87. 2. Vectores en el plano. Vector fijo.
 Suma de vectores.
Ejercicio: Calcula gráficamente u+v, v+w y u+v+w
Solución:

88. 1. Polígonos
Elementos de un polígono
Triángulos: rectas y puntos notables
Semejanza de polígonos
2. Vectores en el plano
Elementos de un vector
Componentes de un vector
Suma de vectores
3. Transformaciones en el plano
4. Poliedros
5. Perímetro, área y volumen
TEMA 7.Geometría.

89. 3. Transformaciones en el plano.
 Traslación: Mover un elemento según un vector de
traslación.

90. 3. Transformaciones en el plano.
 Traslación: Mover un elemento según un vector de
traslación.
Método gráfico u
Trasladar la figura ABC según el vector director .

91. 3. Transformaciones en el plano.
 Traslación: Mover un elemento según un vector de
traslación.
Método gráfico u
Trasladar la figura ABC según el vector director .

92. 3. Transformaciones en el plano.
 Traslación: Mover un elemento según un vector de
traslación.
Método gráfico u
Trasladar la figura ABC según el vector director .

93. 3. Transformaciones en el plano.
 Traslación: Mover un elemento según un vector de
traslación.
Método gráfico u
Trasladar la figura ABC según el vector director .

94. 3. Transformaciones en el plano.
 Traslación sucesiva.
Método gráfico u v
Trasladar la figura ABC según los vectores directores y
.

95. 3. Transformaciones en el plano.
 Traslación sucesiva.
Método gráfico u v
Trasladar la figura ABC según los vectores directores y
.

96. 3. Transformaciones en el plano.
 Traslación sucesiva.
Método gráfico u v
Trasladar la figura ABC según los vectores directores y
.

97. 3. Transformaciones en el plano.
 Traslación sucesiva.
Método gráfico u v
Trasladar la figura ABC según los vectores directores y
.

98. 3. Transformaciones en el plano.
 Traslación.
Ejercicio: Traslada la figura según el vector v
director .

99. 3. Transformaciones en el plano.
 Traslación.
Ejercicio: Traslada la figura según el vector v
director .
Solución:

100. 3. Transformaciones en el plano.
 Traslación.
Ejercicio: Traslada la figura según el vector v
director .
Solución:

101. 3. Transformaciones en el plano.
 Traslación.
Ejercicio: Traslada la figura según el vector v
director .
Solución:

102. 3. Transformaciones en el plano.
 Traslación: Mover un elemento según un vector de
traslación.
Método u
Trasladar la figura MNP según el vector director .
analítico
M(-2, 5) N(0, 3) P(4,6)
u(2, 6)

103. 3. Transformaciones en el plano.
 Traslación: Mover un elemento según un vector de
traslación.
Método u
Trasladar la figura MNP según el vector director .
analítico
M(-2, 5) N(0, 3) P(4,6)
u(2, 6)
M’= M+u = (-2, 5)+(2, 6)=(-2+2, 5+6) = (0, 11)
N’ = N+u = (0, 3)+(2, 6)=(0+2, 3+6) = (2, 9)
P’ = P+u = (4,6)+(2, 6)=(4+2, 6+6) = (6, 12)

104. 3. Transformaciones en el plano.
 Traslación.
v
Ejercicio: Calcula las coordenadas del polígono FGH desplazado según el
vector . F(0, -5) G(-1, 1) H(6,0)
v(-2, -5)

105. 3. Transformaciones en el plano.
 Traslación.
v
Ejercicio: Calcula las coordenadas del polígono FGH desplazado según el
vector . F(0, -5) G(-1, 1) H(6,0)
v(-2, -5)
Solución:
F’ = F+v = (0, -5)+(-2, -5) = (0-2, -5-5) = (-2, -10)
G’ = G+v = (-1, 1)+(-2, -5) = (-1-2, 1-5) = (-3, -4)
H’ = H+v = (6, 0)+(-2, -5) = (6-2, 0-5) = (4, -5)

106. 3. Transformaciones en el plano.
 Giro: Rotación de un elemento con respecto a un
Para definir el fijo.de cualquier elemento necesitamos un centro de giro y un
punto giro
ángulo de giro.

107. 3. Transformaciones en el plano.
 Giro.
Para definir el giro de cualquier elemento necesitamos un centro de giro y un
ángulo de giro.

108. 3. Transformaciones en el plano.
 Giro.
Para definir el giro de cualquier elemento necesitamos un centro de giro y un
ángulo de giro.

109. 3. Transformaciones en el plano.
 Giro.
Para definir el giro de cualquier elemento necesitamos un centro de giro y un
ángulo de giro.

110. 3. Transformaciones en el plano.
 Giros sucesivos.

111. 3. Transformaciones en el plano.
 Giros sucesivos.
Para definir giros sucesivos necesitamos dos centros de giro y dos ángulo de
giro.

112. 3. Transformaciones en el plano.
 Giros sucesivos.
Para definir giros sucesivos necesitamos dos centros de giro y dos ángulo de
giro.

113. 3. Transformaciones en el plano.
 Giros sucesivos.
Para definir giros sucesivos necesitamos dos centros de giro y dos ángulo de
giro.

114. 3. Transformaciones en el plano.
 Giros sucesivos.
Ejercicio: Gira la figura ABCDEF -90º con respecto al punto O.

115. 3. Transformaciones en el plano.
 Giros sucesivos.
Ejercicio: Gira la figura ABCDEF -90º con respecto al punto O.
Solución:

116. 3. Transformaciones en el plano.
 Simetría.
Simetría axial: Cada punto de la nueva figura está a la misma distancia del eje
de simetría

117. 3. Transformaciones en el plano.
 Simetría.
Simetría axial: Cada punto de la nueva figura está a la misma distancia del eje
de simetría

118. 3. Transformaciones en el plano.
 Simetría.
Simetría axial: Cada punto de la nueva figura está a la misma distancia del eje
de simetría

119. 3. Transformaciones en el plano.
 Simetría.
Simetría axial: Cada punto de la nueva figura está a la misma distancia del eje
de simetría

120. 3. Transformaciones en el plano.
 Simetría.
Simetría axial: Cada punto de la nueva figura está a la misma distancia del eje
de simetría

121. 3. Transformaciones en el plano.
 Simetría.
Simetría axial: Cada punto de la nueva figura está a la misma distancia del eje
de simetría

122. 3. Transformaciones en el plano.
 Simetría.
Simetría axial: Cada punto de la nueva figura está a la misma distancia del eje
de simetría

123. 3. Transformaciones en el plano.
 Simetría.
Simetría axial: Cada punto de la nueva figura está a la misma distancia del eje
de simetría

124. 3. Transformaciones en el plano.
 Simetría.
Simetría axial: Cada punto de la nueva figura está a la misma distancia del eje
de simetría

125. 3. Transformaciones en el plano.
 Simetría.
Simetría axial.
Ejercicio: Dibuja la figura simétrica respecto del eje dibujado.

126. 3. Transformaciones en el plano.
 Simetría.
Simetría axial.
Ejercicio: Dibuja la figura simétrica respecto del eje dibujado.
Solución:

127. 3. Transformaciones en el plano.
 Simetría.
Simetría central: Cada punto de la nueva figura está a la misma distancia del
centro de simetría y sobre la misma recta.

128. 3. Transformaciones en el plano.
 Simetría.
Simetría central: Cada punto de la nueva figura está a la misma distancia del
centro de simetría y sobre la misma recta.

129. 3. Transformaciones en el plano.
 Simetría.
Simetría central: Cada punto de la nueva figura está a la misma distancia del
centro de simetría y sobre la misma recta.

130. 3. Transformaciones en el plano.
 Simetría.
Simetría central: Cada punto de la nueva figura está a la misma distancia del
centro de simetría y sobre la misma recta.

131. 3. Transformaciones en el plano.
 Simetría.
Simetría central: Cada punto de la nueva figura está a la misma distancia del
centro de simetría y sobre la misma recta.

132. 3. Transformaciones en el plano.
 Simetría.
Simetría central: Cada punto de la nueva figura está a la misma distancia del
centro de simetría y sobre la misma recta.

133. 3. Transformaciones en el plano.
 Simetría.
Simetría central: Cada punto de la nueva figura está a la misma distancia del
centro de simetría y sobre la misma recta.

134. 3. Transformaciones en el plano.
 Simetría.
Simetría central: Cada punto de la nueva figura está a la misma distancia del
centro de simetría y sobre la misma recta.

135. 3. Transformaciones en el plano.
 Simetría.
Simetría central: Cada punto de la nueva figura está a la misma distancia del
centro de simetría y sobre la misma recta.

136. 3. Transformaciones en el plano.
 Simetría.
Simetría central.
Ejercicio: Dibuja la figura simétrica respecto al punto O.

137. 3. Transformaciones en el plano.
 Simetría.
Simetría central.
Ejercicio: Dibuja la figura simétrica respecto al punto O.
Solución:

138. 3. Transformaciones en el plano.
 Simetría.
Ejes de simetría en figuras.

139. 3. Transformaciones en el plano.
 Simetría.
Ejes de simetría en figuras.

140. 3. Transformaciones en el plano.
 Simetría.
Ejes de simetría en figuras.

141. 3. Transformaciones en el plano.
 Simetría.
Ejes de simetría en figuras.

142. 3. Transformaciones en el plano.
 Simetría.
Ejes de simetría en figuras.

143. 3. Transformaciones en el plano.
 Simetría.
Ejes de simetría en figuras.

144. 3. Transformaciones en el plano.
 Simetría.
Ejes de simetría en figuras.

145. 3. Transformaciones en el plano.
 Simetría.
Ejes de simetría en figuras.

146. 3. Transformaciones en el plano.
 Simetría.
Ejes de simetría en figuras.

147. 3. Transformaciones en el plano.
 Simetría.
Ejes de simetría en figuras.

148. 3. Transformaciones en el plano.
 Simetría.
Ejes de simetría en figuras.

149. 3. Transformaciones en el plano.
 Simetría.
Centro de simetría en figuras.

150. 3. Transformaciones en el plano.
 Simetría.
Centro de simetría en figuras.

151. 3. Transformaciones en el plano.
 Simetría.
Centro de simetría en figuras.

152. 3. Transformaciones en el plano.
 Simetría.
Centro de simetría en figuras.

153. 3. Transformaciones en el plano.
 Simetría.
Centro de simetría en figuras.

154. 3. Transformaciones en el plano.
 Simetría.
Centro de simetría en figuras.

155. 3. Transformaciones en el plano.
 Simetría.
Centro de simetría en figuras.

156. 3. Transformaciones en el plano.
 Simetría.
Centro de simetría en figuras.

157. 3. Transformaciones en el plano.
 Simetría.
Centro de simetría en figuras.

158. 1. Polígonos
Elementos de un polígono
Triángulos: rectas y puntos notables
Semejanza de polígonos
2. Vectores en el plano
Elementos de un vector
Componentes de un vector
Suma de vectores
3. Transformaciones en el plano
Traslación, giro y simetría
4. Poliedros
5. Perímetro, área y volumen
TEMA 7.Geometría.

159. 4. Poliedros.
 Poliedro: Cuerpo geométrico limitado por cuatro o
más polígonos planos.

160. 4. Poliedros.
 Elementos de un poliedro.
vértice
cara

161. 4. Poliedros.
 Poliedros regulares (sólidos platónicos).

162. 4. Poliedros.
 Cóncavo y convexo
Convexo Cóncavo
Ninguna cara, al Alguna cara, al prolongarla,
prolongarla, corta al poliedro. corta al poliedro.
Se puede apoyar sobre un Tiene alguna cara que no se
plano por cualquiera de sus puede apoyar sobre un plano.
caras.

163. 4. Poliedros.
 Fórmula de Euler
C + V = A +2
CARAS + VÉRTICES =
ARISTAS + 2

164. 4. Poliedros.
 Fórmula de Euler
C + V = A +2
CARAS + VÉRTICES =
ARISTAS + 2
2 2
1 3
Caras = 4
1 1
Vértices = 4
3 4 Aristas = 6
3 2
5 Fórmula de Euler
4+4=6+2
4
6
4

165. 4. Poliedros.
 Prismas y pirámides
PRISMA PIRÁMIDE
Apotema
lateral
Apotema
de la base Apotema
de la base
Poliedro cuyas bases son Poliedro cuya base es un
polígonos iguales y polígono y cuyas caras son
paralelos triángulos

166. 4. Poliedros.
 Prismas y pirámides
PRISMA OBLICUO PIRÁMIDE
OBLICUA
Alguna de sus caras no es Alguna de sus caras no es un
un rectángulo triángulo isósceles

167. 4. Poliedros.
 Teorema de Pitágoras en el espacio
D = a2 + b2 + c2
d
a
d = a2 + c2
c

168. 4. Poliedros.
 Teorema de Pitágoras en el espacio
Ejercicio: Halla las diagonales D y d.
a=5cm
b=4cm
c=10cm

169. 4. Poliedros.
 Teorema de Pitágoras en el espacio
Ejercicio: Halla las diagonales D y d.
a=5cm
b=4cm
c=10cm
Solución:
d= a2 + c2 = 52 + 102 = 25 + 100 = 125 = 1118cm
,
D= a2 + b2 + c2 = 52 + 42 + 102 = 25 + 16 + 100 = 141= 1187cm
,

170. 4. Poliedros.
 Teorema de Pitágoras en el espacio
Ejercicio: Halla la apotema de la pirámide ap.
h=12cm
B=5cm
ap
B

171. 4. Poliedros.
 Teorema de Pitágoras en el espacio
Ejercicio: Halla la apotema de la pirámide ap.
h=12cm
B=5cm
ap
ap 12cm
2.5cm
ap = 122 + 2,52 = 144 + 6,25
B
= 150,25 = 12,25cm

172. 4. Poliedros.
 Cuerpos redondos
CILINDRO ESFERA
CONO
TRONCO DE CONO

173. 1. Polígonos
Elementos de un polígono
Triángulos: rectas y puntos notables
Semejanza de polígonos
2. Vectores en el plano
Elementos de un vector
Componentes de un vector
Suma de vectores
3. Transformaciones en el plano
Traslación, giro y simetría
4. Poliedros y cuerpos redondos
5. Perímetro, área y volumen
TEMA 7.Geometría.

174. 5. Perímetro, área y volumen.
 Fórmulas de área y perímetro de figuras planas.

175. 5. Perímetro, área y volumen.
 Polígonos.
Perímetro de un polígono: Suma de la longitud de todos sus lados
P = 4+1,5+2+3+0,5 = 11cm

176. 5. Perímetro, área y volumen.
 Polígonos.
Área de un polígono: Superficie que encierra el polígono
A = Arectángulo + Atriángulo =
= 12·4 + (12·5/2) =
= 48 + 30 = 78 m2

177. 5. Perímetro, área y volumen.
 Polígonos.
Ejercicio: Halla el perímetro y el área de la siguiente figura.
10cm

178. 5. Perímetro, área y volumen.
 Polígonos.
Ejercicio: Halla el perímetro y el área de la siguiente figura.
10cm Solución:
Perímetro
P = 10+20+10+(2π10)/2 =
= 40+31,4 = 71,4 cm
20cm
Área
A = Arectángulo+Asemicircunferencia =
= 10·20 + (π102)/2 =
10cm
= 200 + 157,08 = 357,08 cm2

179. 5. Perímetro, área y volumen.
 Fórmulas de área de cuerpos geométricos.

180. 5. Perímetro, área y volumen.
 Fórmulas de volumen de cuerpos geométricos.

181. 5. Perímetro, área y volumen.
 Fórmulas de volumen y área de cuerpos geométricos.
Ejercicio: Halla el área y el volumen de la siguiente figura.

182. 5. Perímetro, área y volumen.
 Fórmulas de volumen y área de cuerpos geométricos.
Ejercicio: Halla el área y el volumen de la siguiente figura.
Solución:Área
AL (Lateral)
p=6·10=60cm
Apotema
Pitágoras
A= 252 - 52 =
A
= 625 - 25 =
= 600 = 24,5cm
60·24,5 2
AL = = 735cm
2

183. 5. Perímetro, área y volumen.
 Fórmulas de volumen y área de cuerpos geométricos.
Ejercicio: Halla el área y el volumen de la siguiente figura.
Solución:Área
ABase
10
Pitágoras p·a
a= 2
10 - 5 = 2 ABase = =
2
2 60·8,66
AL = 735 cm = 100 - 25 = = =
2
= 75 = 8,66cm
2
= 259,8 cm

184. 5. Perímetro, área y volumen.
 Fórmulas de volumen y área de cuerpos geométricos.
Ejercicio: Halla el área y el volumen de la siguiente figura.
Solución:Área
2
AL = 735cm
ABase = 259,8 2
cm
2
AT = AL + ABase = 735+ 259,8= 994,8 cm

185. 5. Perímetro, área y volumen.
 Fórmulas de volumen y área de cuerpos geométricos.
Ejercicio: Halla el área y el volumen de la siguiente figura.
Solución:Volumen
h - altura
Pitágoras
h= 252 - 102 =
25
h = 625- 100 =
= 525 = 22,91cm
10
ABase·h 259,8·22,9
1 3
V= = = 1983,14 cm
3 3