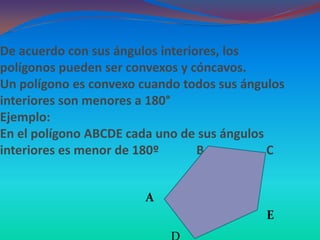
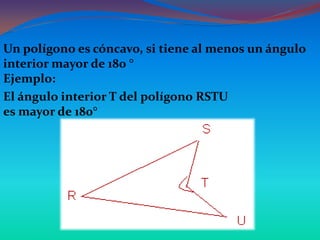
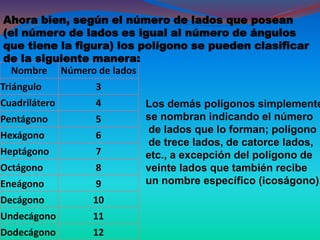
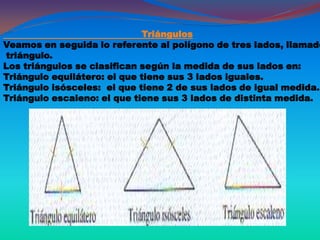
Este documento describe las figuras geométricas básicas como el punto, la línea, el plano y la superficie, y cómo se combinan para formar figuras geométricas más complejas. Explica que las figuras geométricas se definen como espacios cerrados por líneas o superficies, y clasifica las figuras de acuerdo a sus lados (polígonos) y formas (cuerpos geométricos). También proporciona detalles sobre cómo clasificar polígonos específicos como triángulos y cuadriláteros

2. En la geometría, como disciplina, se distinguen
componentes tales como el plano, el punto, la línea -
recta, curva, quebrada-, la superficie, el segmento y
otros de cuya combinación nacen todas las figuras
geométricas.
El patio de tu escuela, una cancha de fútbol, los
muebles de una casa o una tuerca son algunos de los
innumerables ejemplos en donde se pueden apreciar
figuras geométricas.
Entonces, una figura geométrica (también se la
puede denominar lugar geométrico) corresponde a
un espacio cerrado por líneas o por superficies.
Las figuras geométricas de lados rectos se
denominan polígono y las figuras de lados curvos se
denominan círculo y circunferencia y corresponden
también a polígonos.

3. Es importante recordar que las formas sólidas
o tridimensionales corresponden a los cuerpos
geométricos y se denominan poliedros, como e
cubo y la pirámide, y a los cuerpos
redondos, como la esfera y el cilindro.
Según las características de las figuras
geométricas (polígonos) se pueden establecer
varias clasificaciones.
Según la medida de sus lados y ángulos, los
polígonos pueden ser regulares e irregulares.
Un polígono es regular si todos sus lados
poseen la misma longitud y si todos sus
ángulos son iguales.

4. Ejemplos:
Polígonos regulares

5. Un polígono es irregular si todos sus
lados tienen longitudes diferentes al igual
que la medida de sus ángulos.
Ejemplos:
 Lados diferentes Ángulos diferentes

6. De acuerdo con sus ángulos interiores, los
polígonos pueden ser convexos y cóncavos.
Un polígono es convexo cuando todos sus ángulos
interiores son menores a 180°
Ejemplo:
En el polígono ABCDE cada uno de sus ángulos
interiores es menor de 180º B C
A
E

7. Un polígono es cóncavo, si tiene al menos un ángulo
interior mayor de 180 °
Ejemplo:
El ángulo interior T del polígono RSTU
es mayor de 180°

8. Ahora bien, según el número de lados que posean
(el número de lados es igual al número de ángulos
que tiene la figura) los polígono se pueden clasificar
de la siguiente manera:
Nombre Número de lados
Triángulo 3
Cuadrilátero 4 Los demás polígonos simplemente
Pentágono 5 se nombran indicando el número
de lados que lo forman; polígono
Hexágono 6
de trece lados, de catorce lados,
Heptágono 7 etc., a excepción del polígono de
Octágono 8 veinte lados que también recibe
Eneágono 9 un nombre específico (icoságono).
Decágono 10
Undecágono 11
Dodecágono 12

9. Triángulos
Veamos en seguida lo referente al polígono de tres lados, llamado
triángulo.
Los triángulos se clasifican según la medida de sus lados en:
Triángulo equilátero: el que tiene sus 3 lados iguales.
Triángulo isósceles: el que tiene 2 de sus lados de igual medida.
Triángulo escaleno: el que tiene sus 3 lados de distinta medida.

10. Los triángulos también se pueden clasificar según la
medida de sus ángulos en:
Triángulo acutángulo: el que tiene sus 3 ángulos
agudos (menores de 90º)
Triángulo rectángulo: el que tiene 1 ángulo recto
(90º)
Triángulo obtusángulo: el que tiene 1 ángulo obtuso
(mayor de 90º y menos que 180º)

11. Cuadriláteros
Otro de los polígonos muy populares son los cuadriláteros, los
cuales se clasifican en:
Paralelogramos: son aquellos que tiene 2 pares de lados
paralelos (cuadrado, rectángulo, rombo y romboide)
Trapecios: son aquellos que tienen 1 par de lados paralelos
trapecio isósceles: 2 lados de igual medida, 2 ángulos basales
iguales
trapecio trisolátero: 3 lados de igual medida, 2 pares de
ángulos basales iguales
trapecio rectángulo: ángulos basales rectos (90º)
trapecio escaleno: lados y ángulos de distinta medida
Trapezoides: No tienen lados paralelos
trapezoide simétrico: 2 lados de igual medida
trapezoide asimétrico: todos los lados de distinta medida
Conocer las características de los polígonos ayuda para el
estudio de muchos temas como perímetros y áreas entre otros.