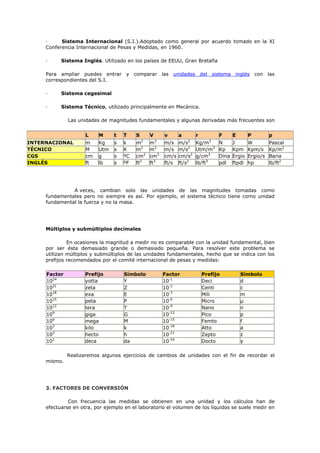
Este documento introduce los conceptos básicos de medición y unidades de medida. Explica que la medición implica comparar una magnitud física con una unidad adoptada como patrón. Luego describe el Sistema Internacional de Unidades (SI) y sus unidades fundamentales de longitud, masa, tiempo, etc. Finalmente, cubre temas como unidades derivadas, factores de conversión y diferentes sistemas de unidades.

2. 1. INTRODUCCIÓN
La observación de un fenómeno es en general incompleta a menos que dé lugar a
una información cuantitativa. Para obtener dicha información se requiere la medición de una
propiedad física. Así, la medición constituye una buena parte de la rutina diaria del físico
experimental.
La medición es la técnica por medio de la cual asignamos un número a una
propiedad física, como resultado de una comparación de dicha propiedad con otra similar
tomada como patrón, la cual se ha adoptado como unidad.
Supongamos una habitación cuyo suelo está cubierto de baldosas, tal como se ve
en la figura, tomando una baldosa como unidad, y contando el número de baldosas medimos
la superficie de la habitación, 30 baldosas. En la figura de la derecha la medida de la misma
superficie da un resultado diferente, ahora contamos15 baldosas .
Y es que la medida de una misma magnitud física (una superficie) da lugar a dos
cantidades distintas debido a que se han empleado distintas unidades de medida.
Este ejemplo, nos pone de manifiesto la necesidad de establecer una única unidad
de medida para una magnitud dada, de modo que la información sea comprendida por
todas las personas.
Este es el motivo de la existencia del Sistema Internacional de Unidades de
medida, obligatorio en España y vigente en la Unión Europea (REAL DECRETO 1317/1989, de
27 de octubre de 1989 por el que se establecen las Unidades Legales de Medida, publicado el
3 de noviembre)
1 Magnitudes fundamentales y derivadas
Sabemos que la física, lo mismo que la química se apoyan en la experimentación y
para llevarla a cabo se necesita de la medida. Algunas pueden realizarse manualmente, pero
en la mayoría de los casos se llevan a cabo mediante aparatos, que las indican mediante una
aguja, electrónicamente de forma digital, ó registrándolas...
En este módulo la tarea que nos ocupa es la de aprender a realizar ensayos,
pruebas, a realizarlos correctamente, según norma y a notificarlos de manera adecuada
utilizando la notación científica y expresando su valor y su incertidumbre en la unidad
adecuada. Es por esto que necesitamos conocer de manera correcta la expresión de las
medidas y los sistemas de unidades internacionalmente adoptados.

3. Empezaremos por identificar aquello que medimos y le llamaremos Magnitud.
Por lo tanto, definimos magnitud como todo aquello que se puede medir. Son
magnitudes el tiempo, la masa, la longitud, etc.. La cualidad fundamental que ha de tener
una magnitud es que las cantidades puedan ser comparadas entre sí
Medir una magnitud es compararla con otra de la misma naturaleza, llamada
unidad, para averiguar el número de veces que la contiene.
Medir es contar cuántas veces la unidad está comprendida en la magnitud que se
mide.
Llamaremos magnitudes fundamentales a aquellas que no necesitan de otras
para ser definidas y cuyas unidades son fáciles de construir y emplear.

4. Cuando una magnitud se define en función de las fundamentales diremos que es
una magnitud derivada
El conocimiento de cualquier magnitud se reduce a la medida de unas pocas
magnitudes escogidas como fundamentales por ser fáciles de determinar. Las ecuaciones de
definición indican cómo se relacionan entre sí las magnitudes fundamentales para dar una
medida derivada.
Llamamos ecuación de dimensiones de una magnitud derivada a aquella expresión
que indica la dependencia entre la magnitud derivada y las fundamentales. Se obtiene a
partir de las ecuaciones de definición por sucesivas sustituciones de las magnitudes que
intervienen en ella, por las ecuaciones de definición correspondientes, hasta lograr que la
expresión dependa únicamente de magnitudes fundamentales. Las magnitudes se escribirán
en mayúsculas.
Así la superficie, el volumen, la velocidad y la densidad tienen las ecuaciones de
dimensión:
S = L2
V = L 3
v = L T -1
ρ = M L -3
Ejercicio 1
Escribe la ecuación de dimensiones de:
Presión:
P=F/S
Recordamos que la fuerza es el producto de la masa y la aceleración
Viscosidad
η=F*L/S*V
Tensión superficial
s=F/L
Estas relaciones matemáticas han de cumplir el principio de homogeneidad: una
ecuación es homogénea cuando los dos miembros de la misma, tienen idéntica expresión
en unidades fundamentales del sistema internacional; de este modo comprobamos que la
ecuación de dimensiones es imprescindible para demostrar la homogeneidad en las
ecuaciones, es la forma de asegurarnos de que estamos igualando expresiones coherentes,
que con tienen las mismas magnitudes en ambas partes de la igualdad.
Así por ejemplo, para conocer si las unidades atmósfera x litro, pertenecen a la
magnitud fuerza, trabajo ó presión, determinaremos su ecuación dimensional. Sabemos que
las atmósferas son unidad de presión y por lo tanto:

5. atmósferas · litro = ( M · L-1
·T-2
) · (L3
) = M · L-1
· T-2
)
Esta ecuación de dimensiones se corresponde con un trabajo ó energía.
Ejercicio 2
Comprobar la homogeneidad de las ecuaciones físicas:
F t = Mv
Ec = Ep
P = F / v
2. UNIDADES. SISTEMAS DE UNIDADES.
Según las magnitudes que se adopten como fundamentales y las unidades en que
se midan, se construyen distintos sistemas de unidades, así el Sistema Internacional
adopta como fundamentales longitud, masa, tiempo y otras que veremos. Por todo esto
concluimos que, al conjunto de magnitudes adoptadas como fundamentales y sus derivadas,
así como las unidades en que se miden se llama sistema de unidades.
Ya hemos definido la unidad como la cantidad de magnitud que tomamos, de
forma arbitraria, como término de comparación al efectuar una medida; un trozo de cuerda
de una longitud determinada por ejemplo, el problema es que así nuestros datos no tendrían
significado para los demás.
Condiciones
Para que una unidad de medida sea considerada como tal debe cumplir una serie
de condiciones:
· Que sea fácil y económica de reproducir en cualquier lugar
· Que posea un grado de precisión aceptable
· Que sea inalterable.
Cada magnitud lleva asociada una o varias unidades, así :
Longitud: metro, pies,

6. Volumen: l, m3
, pie cúbico, galones, barriles...
Para poder usarlas con corrección es necesario conocerlas, saber qué relaciones hay
entre ellas...
Unidades SI básicas
Magnitud Nombre Símbolo
Longitud metro m
Masa kilogramo kg
Tiempo segundo s
Intensidad de corriente eléctrica ampere A
Temperatura termodinámica kelvin K
Cantidad de sustancia mol mol
Intensidad luminosa candela cd
Unidad de longitud:
metro (m)
El metro es la longitud de trayecto recorrido en el vacío por
la luz durante un tiempo de 1/299 792 458 de segundo.
Unidad de masa El kilogramo (kg) es igual a la masa del prototipo
internacional del kilogramo
Unidad de tiempo El segundo (s) es la duración de 9 192 631 770 periodos de
la radiación correspondiente a la transición entre los dos
niveles hiperfinos del estado fundamental del átomo de cesio
133.
Unidad de intensidad de
corriente eléctrica
El amperio (A) es la intensidad de una corriente constante
que manteniéndose en dos conductores paralelos,
rectilíneos, de longitud infinita, de sección circular
despreciable y situados a una distancia de un metro uno de
otro en el vacío, produciría una fuerza igual a 2·10-7
newton
por metro de longitud.
Unidad de temperatura
termodinámica
El kelvin (K), unidad de temperatura termodinámica, es la
fracción 1/273,16 de la temperatura termodinámica del
punto triple del agua.
Observación: Además de la temperatura termodinámica
(símbolo T) expresada en kelvins, se utiliza también la
temperatura Celsius (símbolo t) definida por la ecuación t =
T - T0 donde T0 = 273,15 K por definición.
Unidad de cantidad de
sustancia
El mol (mol) es la cantidad de sustancia de un sistema que
contiene tantas entidades elementales como átomos hay en
0,012 kilogramos de carbono 12.
Cuando se emplee el mol, deben especificarse las unidades
elementales, que pueden ser átomos, moléculas, iones,
electrones u otras partículas o grupos especificados de tales
partículas.
Unidad de intensidad
luminosa
La candela (cd) es la unidad luminosa, en una dirección
dada, de una fuente que emite una radiación monocromática
de frecuencia 540·1012
hertz y cuya intensidad energética en
dicha dirección es 1/683 watt por estereorradián.

7. Unidades SI suplementarias.
Magnitud Nombre Símbolo Expresión en unidades SI
básicas
Ángulo plano Radián rad mm-1
= 1
Ángulo sólido Estereorradián sr m2
m-2
= 1
Unidad de
ángulo plano
El radián (rad) es el ángulo plano comprendido entre dos
radios de un círculo que, sobre la circunferencia de dicho
círculo, interceptan un arco de longitud igual a la del radio.
Unidad de
ángulo sólido
El estereorradián (sr) es el ángulo sólido que, teniendo su
vértice en el centro de una esfera, intercepta sobre la superficie
de dicha esfera un área igual a la de un cuadrado que tenga por
lado el radio de la esfera.
Unidades SI derivadas
Las unidades SI derivadas se definen de forma que sean coherentes con las
unidades básicas y suplementarias, es decir, se definen por expresiones algebraicas bajo la
forma de productos de potencias de las unidades SI básicas y/o suplementarias con un factor
numérico igual 1.
Varias de estas unidades SI derivadas se expresan simplemente a partir de las
unidades SI básicas y suplementarias. Otras han recibido un nombre especial y un símbolo
particular.
Si una unidad SI derivada puede expresarse de varias formas equivalentes
utilizando, bien nombres de unidades básicas y suplementarias, o bien nombres especiales
de otras unidades SI derivadas, se admite el empleo preferencial de ciertas combinaciones o
de ciertos nombres especiales, con el fin de facilitar la distinción entre magnitudes que
tengan las mismas dimensiones. Por ejemplo, el hertz se emplea para la frecuencia, con
preferencia al segundo a la potencia menos uno, y para el momento de fuerza, se prefiere el
newton metro al joule.
Unidades SI derivadas expresadas a partir de unidades básicas y
suplementarias.
Magnitud Nombre Símbolo
Superficie metro cuadrado m2
Volumen metro cúbico m3
Velocidad metro por segundo m/s
Aceleración metro por segundo cuadrado m/s2
Número de ondas metro a la potencia menos uno m-1
Masa en volumen kilogramo por metro cúbico kg/m3
Velocidad angular radián por segundo rad/s
Aceleración angular radián por segundo cuadrado rad/s2
Además de las vistas también puedes acceder a Unidades SI derivadas con
nombres y símbolos especiales
Recordamos que en función de las magnitudes y de las unidades tomadas, existen
distintos sistemas de unidades que son ,

8. · Sistema Internacional (S.I.).Adoptado como general por acuerdo tomado en la XI
Conferencia Internacional de Pesas y Medidas, en 1960.
· Sistema Inglés. Utilizado en los países de EEUU, Gran Bretaña
Para ampliar puedes entrar y comparar las unidades del sistema inglés con las
correspondientes del S.I.
· Sistema cegesimal
· Sistema Técnico, utilizado principalmente en Mecánica.
Las unidades de magnitudes fundamentales y algunas derivadas más frecuentes son
L M t T S V v a r F E P p
INTERNACIONAL m Kg s k m2
m3
m/s m/s2
Kg/m3
N J W Pascal
TÉCNICO M Utm s K m2
m3
m/s m/s2
Utm/m3
Kp Kpm Kpm/s Kp/m2
CGS cm g s ºC cm2
cm3
cm/s cm/s2
g/cm3
Dina Ergio Ergio/s Baria
INGLÉS ft lb s ºF ft2
ft3
ft/s ft/s2
lb/ft3
pdl ftpdl hp lb/ft2
A veces, cambian solo las unidades de las magnitudes tomadas como
fundamentales pero no siempre es así. Por ejemplo, el sistema técnico tiene como unidad
fundamental la fuerza y no la masa.
Múltiplos y submúltiplos decimales
En ocasiones la magnitud a medir no es comparable con la unidad fundamental, bien
por ser ésta demasiado grande o demasiado pequeña. Para resolver este problema se
utilizan múltiplos y submúltiplos de las unidades fundamentales, hecho que se indica con los
prefijos recomendados por el comité internacional de pesas y medidas:
Factor Prefijo Símbolo Factor Prefijo Símbolo
1024
yotta Y 10-1
Deci d
1021
zeta Z 10-2
Centi c
1018
exa E 10-3
Mili m
1015
peta P 10-6
Micro µ
1012
tera T 10-9
Nano n
109
giga G 10-12
Pico p
106
mega M 10-15
Femto f
103
kilo k 10-18
Atto a
102
hecto h 10-21
Zepto z
101
deca da 10-24
Docto y
Realizaremos algunos ejercicios de cambios de unidades con el fin de recordar el
mismo.
3. FACTORES DE CONVERSIÓN
Con frecuencia las medidas se obtienen en una unidad y los cálculos han de
efectuarse en otra, por ejemplo en el laboratorio el volumen de los líquidos se suele medir en

9. cm3
y para cálculos posteriores debe expresarse esa cantidad en litros, el cambio en este
caso es muy sencillo, basta con recordar que
1l = 1000 cm3
En otros será algo más complicado y tendremos que usar factores de conversión:
36 Km / h --> m / s
36 * * = 10
Ejercicio 3 Efectúa los siguientes cambios de unidades
5hg g
9·109
m Km
0,04m2
mm2
5mm m
2cm3
m3
2,3g Kg
Ejercicio 4 Expresa en la unidad correspondiente del sistema Internacional
48cm ; 2cm2
; 0,63g ; 200,3 mm3
;
Ejercicio 5 Escribir en unidades del SI las siguientes cantidades usando factores de
conversión:
· 2 g / cm3
· 3000 Kp / cm2
· 90 ml / ( día * Kg)
· 0,082 atm l / mo
· 2 ¾ in
· 25 ergios

10. · 3000 cal
· 250 Kw h
· 68 mm Hg
· 3 atm
· 1125 dina
En principio estos ejercicios son sencillos, aumentando el grado de dificultad si las
unidades de partida pertenecen al sistema inglés; aún debemos dar un paso más, el sistema
inglés hace uso de lo que en matemáticas nosotros hemos estudiado como números
compuestos y números mixtos.
Cuando yo vea una cantidad expresada 2 ¾ in, debo entender que corresponde a 2
pulgadas y ¾ de pulgada.
Para efectuar operaciones sencillas con estas expresiones recordaremos conceptos
sobré operaciones con fracciones:
Otro modo de operar, sería transformando los números mixtos;
Así ; y
Por lo que = in
También hay que tener en cuenta que al no ser un sistema decimal para operar con
cantidades expresadas en unidades inglesas el sistema será similar al que usamos con otras
magnitudes que nos son más familiares, como la medida del tiempo:
Ejemplo:

11. Aplicamos a continuación estos conocimientos efectuando las siguientes
operaciones:
Ejercicio 6:
5 días 9 horas 15 minutos – 1 día 15 horas 40 minutos
8 yd 1 ft 5 in – 3 yd 2 ft 7 in
7 ½ - 4 ¾
INTERPOLACIÓN
Al intentar efectuar una medida en una escala de un dial en ocasiones
encontraremos problemas para dar un valor determinado.
Aprendamos a leer correctamente la medida indicada en los siguientes diales:
Ejercicio 7

12. · 1 125º
· 2 115º
· 3 105º
· 4 75º
· 5 50º
· 1 21,1 mm
· 2 22,1 mm
· 3 23,4 mm
· 4 26,5 mm
· 5 27,6 mm
· 1 5/16 in
· 2 1 2/16 in
· 3 1 9/16 in

13. · 4 2 7/16 in
· A 80
· B 320
· C 520
· A 1,6
· B 6,4
· C 10,4
· A 20
· B 80
· C 130

14. · A 200
· B 800
· C 1400
· A 400
· B 1600
· C 1800
· A 0,4
· B 1,7
. C 2,8
En el caso de una escala en pulgadas:

15. · A 6/ 16 in
· B 1 6/16 in

16. El mismo problema surge al intentar dar un valor a una constante que está tabulada
para valores superiores e inferiores al buscado, por ejemplo:
Sabiendo que la viscosidad de una sustancia es la dada en la tabla adjunta calcular
la viscosidad de la misma a 17 ºC.
Si la variación de la variable en estudio fuese lineal podríamos resolver la cuestión
con una proporción simple, regla de tres, pero si la representamos vemos que no es así.
Aplicando la definición de tangente de un ángulo o la semejanza de triángulos
llegamos a:

17. 4. MEDICIÓN Y CALIBRACIÓN
Hemos definido la acción de medir como comparar una cantidad de una determinada
magnitud con otra de su misma especie que tomamos como patrón.
En general el proceso no es tan simple y se utilizan aparatos de medida. Todo
aparato de medida ha de presentar las siguientes cualidades:
• Rapidez: La respuesta del aparato debe ser lo más rápida posible, no solo para
agilizar el estudio, sino por mantener la constancia de aquellos factores ambientales
cuya variación pueda afectar a la medición. Ejemplo pesada de sustancias
higroscópicas.
• Sensibilidad: Es la mínima cantidad de magnitud que produce una variación en la
señal, ejemplo: distintos tipos de balanza.
• Fidelidad: Un aparato es fiel cuando al medir la misma cantidad se obtiene el mismo
valor.
• Exactitud: Es la concordancia entre las indicaciones del aparato de medida y el valor
verdadero o de referencia aceptado de la magnitud que se mide.
• Precisión: Concordancia existente entre las indicaciones del aparato de medida y
otras indicaciones del mismo aparato al medir la misma magnitud en idénticas
condiciones. Grado de dispersión que presentan los resultados obtenidos al medir
repetidamente un determinado valor de una variable.
Un instrumento es tanto más preciso cuantas más cifras significativas puede
proporcionar y más exacto cuanto más se acerque su lectura al valor proporcionado por
un patrón.
La diferencia entre exactitud y precisión es sencilla si pensamos en un tirador de
armas de fuego, el exacto se aproxima al blanco, el preciso da siempre en el mismo sitio
pero éste no tiene porqué ser el blanco.

18. Calibrado
Para poder determinar si la medida efectuada coincide con el valor
verdadero de la magnitud es necesario conocer la exactitud del aparato, por
buenos que estos sean y aunque se extreme el cuidado y la habilidad,
sabemos que los resultados de medidas sucesivas difieren entre sí en mayor o
menor grado.
Para asegurarnos del perfecto funcionamiento del equipo es necesario calibrarlo. La
calibración forma parte de todo el proceso de análisis y debe tenerse en cuenta en la fase
inicial de diseño o definición del procedimiento experimental.
Existen diferentes métodos de calibración.
• Absolutos: La medida física se relaciona directamente con una cierta cantidad de
magnitud, ejemplo balanza.
• Estequiométricos: Se realiza por medio de una reacción química, usando patrones,
espectrofotómetro.
• Comparativos: Los valores obtenidos se comparan con otros, resultado de repetir la
operación en idénticas condiciones con un patrón, gráficos de control.
5. INEXACTITUD EN LAS MEDIDAS E INCERTIDUMBRE EN LOS RESULTADOS.
ERRORES
En todas las ciencias experimentales se opera con datos numéricos obtenidos a
partir de medidas y observaciones que nunca pueden ser totalmente exactas. Esto se debe a
que ni los instrumentos de medida ni nuestros sentidos son perfectos. Además en muchos
casos intervienen en las fórmulas, números que no pueden tomarse con todas sus cifras;
debemos introducir estos datos con un número determinado de cifras, a este número se
conoce como cifras significativas.
Por ejemplo si nos dicen que una piscina contiene 600 m3
de agua y con un vaso
añadimos 50 ml, ahora el volumen de agua contenido es sin duda de 600,00005 m3
, ¿Es
lógico dar este resultado? No, al medir el volumen inicialmente contenido, el error de la
medida será de varios m3
, carece pues de sentido hablar de milésimas de los mismos.
Del mismo modo, si efectuamos con una balanza analítica una pesada y obtenemos
una lectura de 3,0000 gramos, no deberíamos escribir simplemente “3” ya que la lectura
correcta nos permite cinco cifras significativas sean ceros ó no, debido a la precisión propia
del instrumento.

19. Cifras significativas es el número de cifras válidas en una medida; depende del
instrumento utilizado y de la unidad con que estemos trabajando; incluye todos los dígitos
que pueden ser conocidos de una magnitud; de entre ellos, todos excepto el último son
ciertos y el último estará sujeto a incertidumbre, por tanto en las cifras significativas se
incluye aquella que nos indica el margen de incertidumbre.
Para expresar correctamente los datos experimentales y los resultados finales
consideraremos que :
a. No se han de poner ceros a la derecha de un valor decimal si éstos no son
significativos.
Por ejemplo, con una regla que aprecia décimas de milímetro medimos 218,3 mm,
la expresión de éste resultado es correcta; no lo sería si escribiéramos 218,300 mm ya que
en este caso sólo se aprecia un decimal.
b. Si utilizamos submúltiplos ó múltiplos, los ceros que se derivan no son significativos
y sólo expresan orden de magnitud.
Así, si al realizar una pesada obtuviéramos el valor: 2,1524 gramos y quisiéramos
expresar el resultado en unidades del Sistema Internacional tendríamos: 0,0021524 Kg. En
este resultado no hay ocho cifras significativas, ya que hay tres ceros que indican orden de
magnitud.
Las cifras significativas ligadas a la calidad de la medida son las mismas aunque
cambie el sistema en que se exprese.

20. c. En el registro del valor de una medida o en un cálculo matemático, únicamente
hemos de tomar en consideración todas las cifras de las que estemos seguros, más
aquella que está afectada por la incertidumbre.
d. Es importante diferenciar si un valor corresponde a la expresión de una medida
experimental ó si en cambio se trata de una cantidad obtenida por una expresión
matemática.
Realicemos unos ejemplos:
3.11+21.7= 24.81 este valor no es válido; el correcto sería 24.8
83.12-72= 11.12 igualmente el valor correcto será 11
52.01+37.1-12.875= 76.235 siendo el correcto 76.2
El resultado final cuando se realizan sumas o restas no puede tener más cifras
significativas a la derecha de la coma decimal que las del valor menos preciso.
Si para obtener el valor de la medida realizamos operaciones en las que intervienen
productos y cocientes de datos experimentales deberemos tener en cuenta que el resultado
final no puede tener más cifras significativas que las presentadas por el valor menos preciso.
Así, por ejemplo:
56.70*13.51=766.0
1.83764/1.4=1.3
En el primero de los casos podríamos pensar que el resultado correcto debería tener
2 cifras decimales pero si leemos detenidamente comprenderemos que el resultado debe
tener 4 cifras significativas, que es el número que tienen los factores que intervienen. De
todos modos, es importante profundizar un poco más en esto ya que cuando hablamos de la
precisión de un valor debemos saber calcularlo; en este ejemplo, ¿cuál de los dos valores es
el menos preciso?
Para calcular la precisión:
PA = 0.01/56.70 ; PA =1.76·10-4
PB = 0.01/13.51 ; PB = 7.4·10-4
¿Qué valor es más pequeño? Al valor A le corresponde una precisión menor y el
resultado deberá tener el mismo número de cifras significativas que A.
Existen criterios para determinar el número de cifras significativas que debe tener un
resultado si se obtiene en una operación en la que intervengan logaritmos pero no nos
ocuparemos de ello en este curso.
Ejercicio 8:
Indicar el número de cifras significativas de los siguientes resultados:
a) 0.520 mL
b) 43.2 g
c) 750.0 º C

21. d) 0.3207 Kg
e) 0.3672 g
Ejercicio 9:
Corregir, en caso de ser necesario, el número de cifras significativas de las
operaciones siguientes:
a) 1.021+2.69=3.711
b) 12.4-1.63=10.77
c) 4.34*9.2=39.928
d) (26.14/37.62)*4.38=3.043413
Ejercicio 10:
Calcular el área de un rectángulo cuyos lados son 2.357 m y 1.345 m.
Ejercicio 11:
Calcular la longitud y el área de una circunferencia de radio 0.017 m. Expresa los
resultados en cm y cm2
respectivamente.
Notación científica:
Para expresar cantidades muy grandes o muy pequeñas con un número de cifras
significativas razonable se usa la notación científica. Consiste en escribir cualquier cantidad
como producto de un número comprendido entre 1 y 10 y una potencia entera de 10.
4500 Km = 4,5 10 3
Km
0,002 g = 2 10 -3
g
Al operar con la calculadora introduciremos los datos de esta forma, al acabar los
cálculos nos los puede devolver así o no, en cualquier caso la solución no puede tener más
cifras significativas que los datos de partida.
“El resultado no puede ser más preciso que el dato menos preciso”
Ejemplo: Si la masa de un cuerpo es de 37,50 g y su volumen de 7,00 cm3
calcule
su densidad.
Como regla general diremos que el cálculo se realiza introduciendo todos los datos,
iniciales o intermedios, resultado de otros cálculos, con todas sus cifras, se prevé cuantas
cifras significativas debe tener el resultado y se redondea al valor más cercano.

22. 6. IMPRECISIÓN DE LAS MEDIDAS. CLASIFICACIÓN DE LOS ERRORES
Las medidas realizadas experimentalmente, vienen afectadas de cierta imprecisión,
de modo que cuando medimos varias veces una misma magnitud se obtienen resultados
ligeramente diferentes. Estas imprecisiones son denominadas errores experimentales y es
necesario conocerlos y acotarlos.
Llamamos error a la diferencia existente entre el resultado de una medida
experimental y su valor real.
Los errores son debidos a diversas causas: método utilizado, instrumento de
medida, etc.
Clasificaremos los errores según su tendencia en sistemáticos y aleatorios.
Sistemáticos: Están producidos por un defecto del instrumento de medida o por
una tendencia errónea del observador. Se registran siempre en un mismo sentido, solo
pueden ser puestos de manifiesto cambiando de aparato de medida o de observador.
Los errores sistemáticos tienen las siguientes características:
a. Suelen actuar en un mismo sentido, es decir, o por exceso o por defecto sobre el
valor real.
b. Siempre tienen el mismo valor.
c. pueden ser eliminados si se detecta el motivo del error (utilización de patrones)
d. Afectan a la exactitud de la medida
Aleatorios: Son los debidos a causas imponderables e imposibles de controlar, que
alteran en un sentido o en otro los valores obtenidos; este tipo de errores llamados también
indeterminados o accidentales son difíciles de precisar y eliminar, aunque pueden ser
compensados trabajando con la media de varias determinaciones, como se verá más
adelante.
Las características que los definen son:
a. No aparecen en un solo sentido, sino que lo hacen tanto por exceso como por defecto.
b. Se pueden disminuir si aumentamos la precisión del material y de las técnicas
utilizadas, aunque no pueden ser eliminados porque forman parte del propio proceso de
medida.
c. Se pueden cuantificar y tratar matemáticamente.
d. Afectan a la precisión de la medida
Representando diversas distribuciones de valores de medidas, observaremos
gráficamente la diferencia entre ambos tipos de errores

23. Y según su expresión matemática en absoluto y relativo
Un error de un gramo en una pesada de unos pocos gramos de metal es inadmisible,
mientras que ese mismo valor para la pesada de una tonelada de material es despreciable.
De ahí la necesidad de definir el error relativo y el absoluto.
Definiremos error absoluto cuando nos interesa conocer la magnitud del error en
relación a un valor considerado verdadero o, al menos, correcto y se define
cuantitativamente como la diferencia, con su signo, entre el valor aproximado de la
magnitud, experimental, y el valor verdadero o considerado más correcto, puesto que el
valor verdadero no se conoce.
∆ x = a – x
En la práctica se toma para x el valor medio de un número suficiente de
determinaciones.
Como error absoluto en ocasiones se adopta el valor mínimo que es capaz de medir
el aparato en cuestión, la división de escala.
Por ejemplo cuando realizamos una pesada con una balanza que aprecia hasta el
centigramo admitimos que ∆ x ≤ 0,01 g, o cuando tomamos como valor para p = 3,1416,
con cuatro cifras decimales sabemos que ∆ x ≤ 0,0001.
El error absoluto no sirve para apreciar la precisión de una medida, es decir, el
grado de aproximación de la misma al valor verdadero; para eso es preciso recurrir al error
relativo, que se define como el cociente entre el error absoluto y el valor verdadero de la
magnitud.
e = ∆ x / x

24. Al igual que ocurre con el error absoluto se prefiere conservar el signo para conocer
el sentido del error.
Generalmente, se prefiere expresar el error relativo en tanto por cien.
Tratamiento de errores
Hasta ahora hemos considerado una única medida experimental, por tanto dábamos
como valor de la misma el obtenido más ó menos (+) la precisión del aparato.
En el laboratorio para mejorar la exactitud y la precisión de nuestros resultados no
efectuamos nunca una única medida, ya que aunque los errores accidentales no se pueden
evitar, sabemos que se hayan sujetos a las leyes del azar; y si reiteramos la medida un
número suficiente de veces, utilizando parámetros relativamente sencillos de calcular,
obtendremos información sobre los márgenes entre los cuales se encuentra el valor real con
un cierto grado de probabilidad.
Es importante recordar que el tratamiento de los datos que realizaremos es aplicable
exclusivamente a los errores de tipo aleatorio ya que no podremos obtener buenos
resultados si partimos de datos no fiables o sujetos a errores sistemáticos. En este caso
recurriremos a los patrones y a los controles de calidad para detectar y resolver los errores.
Supongamos que disponemos de una serie de datos sobre una medida.
Para analizarlos convenientemente los agrupamos indicando la frecuencia con la que
aparecen.
Primero agrupamos los resultados y los valores que se repiten, en forma de tabla y
después los representamos gráficamente.
Valor 172 173 174 175 176 177 178
Frecuencia 1 3 5 6 4 2 1
El valor más frecuente se denomina moda, en nuestro caso es el 175. Al valor
central de los obtenidos le llamamos mediana, y media a la suma de todos los resultados
entre el número de determinaciones, que matemáticamente se expresa:

25. =
Estos tres valores alrededor de los cuales se suelen agrupar los datos, son los
parámetros de centralización.
Si observamos la gráfica nos daremos cuenta que los valores aparecen alrededor de
la moda de una forma más o menos simétrica, esto es porque ya hemos comentado que los
errores debidos al azar aparecen por exceso o por defecto con la misma probabilidad.
Los parámetros de dispersión sirven para medir el grado de acercamiento de los
valores. Así, el Rango, es el que mide la amplitud de la serie de datos y se obtiene como el
valor que resulta de los valores extremos superior e inferior de la tabla de datos
experimentales.
Desviación estándar, se define matemáticamente como la raíz cuadrada de la
media aritmética de los cuadrados de las desviaciones absolutas; recordamos que éstas se
calculan como la diferencia, expresada en valor absoluto, entre cada uno de los valores de
la muestra y la media.
Se suele representar por la letra griega sigma s cuando se trabaja con una
población completa, pero si se hace con una serie de datos experimentales (muestra) se
representa por la letra σ, y en ese caso sustituiremos en el denominador el valor de N por N-
1.
σ =
Varianza es un valor ligado a la desviación estándar ya que V = σ2
Ejercicio 12:
Con una regla realizamos 10 medidas del diámetro de un cilindro. Los datos
obtenidos en dm, son los siguientes:
3,78 4,08 4,03 3,93 4,04 3,87 4,05 3,95 3,98 3, 98
Indica el valor de la media, la moda, la mediana y calcula el valor de σ.
Cuanto mayor sea el número de medidas, más simétrica es la gráfica, y en principio,
media, mediana y moda coinciden; a este tipo de distribución le llamamos distribución
normal, pero nuestros datos experimentales no suelen cumplirla tan perfectamente y es
necesario decidir qué valor tomaremos como verdadero cuando los tres de centralización no
coincidan.
Si el número de medidas es suficiente, supuestamente infinito, del diagrama de
barras pasaríamos a una curva continua:

26. Esta curva responde a la ecuación:
Donde: µ , valor verdadero, media
σ desviación estándar =
En esta curva se cumple siempre que:
· 68 % de los datos están en el intervalo µ + σ
· 95 % entre µ + 2 σ
· 99,7 % entre µ + 3 σ
Según estamos observando, el valor de m es un estimador del valor verdadero de la
magnitud y el valor de s nos indica la amplitud del intervalo en que con una probabilidad
predeterminada sabemos que podemos encontrar este valor, así se dice que el valor de la
magnitud buscada es de µ + 2 σ con una probabilidad de un 95%.
El resultado final está expresado en forma de intervalo de confianza, el valor
verdadero se encuentra entre µ - 2 σ y µ+ 2 σ .
Hasta aquí hemos supuesto que habíamos efectuado un número infinito de medidas
de forma que nuestros datos se ajustaban a una Gaussiana, la realidad de nuestro trabajo
será que con número de medidas finito, del orden de tres, cinco, 25 a lo sumo, daremos el
resultado ajustándonos a este modelo con una ligera modificación:

27. En vez de hablar de valor verdadero hablaremos de valor medio indicado por .
En vez de s, desviación estándar, con la ecuación: σ = se usará la
varianza,
= o en su defecto σ;
La única diferencia entre ambas radica en el denominador, en el caso de la
desviación estándar es n y en la varianza es n-1.
A este valor n-1, se llama grados de libertad y se define como el número de medidas
efectuadas menos uno.
Si representásemos los datos en forma de curva no se ajustarían a la de Gauss, por
tanto, se hace necesario introducir un factor de corrección conocido como t de Student que
se halla tabulado para los diferentes grados de libertad y grado de confianza que queramos
dar, el resultado del ensayo se expresará de la forma:
Para decidir cuántas medidas es necesario realizar existen distintos criterios; uno de
ellos, que será el que usaremos en este curso es el siguiente:
1. Como norma siempre efectuamos tres medidas, se calcula la media, xm, la
dispersión, ∆, (diferencia entre las medidas extremas) y el % de dispersión, T,
( * 100=%)
2. Si D ≤ división de escala, se toma xm +∆x
D > división de escala consideramos el valor de T ≤
T ≤ 2 % basta con 3 medidas
2 % < T ≤ 8 % 6 medidas
8 % < T ≤ 15 % 15 medidas
15 % < T 50 medidas
· Por ejemplo, sí al realizar la medida de un portaobjetos obtenemos los siguientes
valores

28. Largo (mm) Ancho(mm) Espesor (mm)
71,05 25,75 1,05
71,00 25,75 1,10
71,10 25,80 1,05
_
Para el largo, calculamos : x = 71,05 s = 0,05 r = 0,01 %D = 0,14
_
Para el ancho, calculamos : x = 25,76 s = 0,02 r = 0,05 %D = 0,08
_
Para el espesor, calculamos: x = 1,06 s = 0,028 r = 0,05 %D = 4,7
Para notificar estos valores, aplicaremos la ecuación y obtendremos:
L = 71,05 ± ; L = 71,05 ± 0,12 mm
A = 25,76 ± ; A = 25,76 ± 0,04 mm
E = 1,06 ± ; E = 1,06 ± 0,04 mm
A la hora de trabajar es más práctico recoger los datos en forma de tabla
Espesor (e) Largo (l) Ancho (a)
X1 1.05 71.05 25.75
X2 1.10 71.00 25.75
X3 1.05 71.10 25.80
D 0.05 0.10;T<2; T(0.10/71.05)·100 0.05
1.0666666 71.05 25.7666
S 0.0288675 0.05 0.0288675
U 0.0939241 0.13749 0.0939241
±U
1.07±0.09 71.05±0.14 25.77±0.09
7. CÁLCULO DE LA INCERTIDUMBRE EN MEDIDAS INDIRECTAS:
Muchas veces nos enfrentaremos a calcular la incertidumbre que acompaña al valor
de una magnitud que no hemos medido directamente, sino que la hemos obtenido a través
de la medida de otras, ligadas a ella por fórmulas conocidas. Para resolverlo vamos a

29. necesitar los valores da la incertidumbre de las magnitudes medidas y aplicar el cálculo de
propagación de incertidumbre. Está muy claro que la incertidumbre que acompañará al
resultado final dependerá de las incertidumbres de todos aquellos factores que
introduzcamos en el cálculo, bien sean datos experimentales, constantes tomadas de tablas
o de certificados de calibración, datos de otros laboratorios...
Estrictamente para una ecuación de medida Y = f (X1 , X2 ,X3..)
la varianza asociada al resultado estaría dada por la expresión:
En esta fórmula el segundo sumando corresponde a las covarianzas y no se aplica
dada la dificultad que entraña su cálculo y su pequeña contribución al resultado final,
además en general usaremos ecuaciones simplificadas para cada caso particular que nos
harán más sencillo el cálculo diario. sumas/ restas
Sumas y restas:
Si en la expresión de partida aparecen magnitudes que deban sumarse ó restarse, la
incertidumbre absoluta del resultado corresponderá a la raíz cuadrada de la suma de las
incertidumbres absolutas de los datos.
La manera más sencilla de expresarlo, en el caso de dos datos, es:
A ± a = (B ± b) + (C ± c)
a = [b2
+ c2
]½
Realicemos algunos ejemplos.
1-Expresar el resultado de la siguiente operación con su intervalo de confianza
correspondiente:
(1,76 ± 0,03) + (1,89 ± 0,02) - (0,554 ± 0,008)
Paso 1. Calculamos el resultado final de los valores prescindiendo de las incertidumbres:
1,76 + 1,89 - 0,554 = 3,096
Paso 2. Calculamos la incertidumbre absoluta del resultado (IA):
IA = [0,032
+ 0,022
+ 0,0082
]½
= 0,0369323...
Paso 3. Expresamos la incertidumbre absoluta del resultado con una sola cifra significativa:
IA = 0,0369323... @ 0,04
Paso 4. Expresamos el resultado final redondeando hasta la posición de la cifra significativa
de su incertidumbre
(1,76 ± 0,03) + (1,89 ± 0,02) - (0,554 ± 0,008) = 3,10 ± 0,04

30. Ya que hemos pasado del valor 3,096 al valor 3,10, puesto que la incertidumbre
tiene su cifra significativa en la segunda cifra decimal y es a esta posición a donde debemos
llegar en la expresión del resultado.
· Ejercicio resuelto:
Calentamos agua y tomamos la tempeatura inicial y final con un termómetro que aprecia
0.5ºC, obteniendo los datos siguientes:
T1=27.0 ± 0.5ºC T2=60.5 ± 0.5ºC
¿cuál es la variación de la temperatura?
T= T2—T1; T=33.5ºC
Para acompañar a este resultado, calculamos: =0.707106..
Por lo tanto daremos como resultado: T=33.5± 0.7
Ejercicio 13:
Calcular las masas moleculares de los siguientes compuestos:
Hipoclorito de sodio NaClO
Sulfato de aluminio Al2(SO4)3
Utilizando los siguientes datos de masas atómicas relativas al 12
C:
Na 22.98977; Al 26.98154
Cl 35.453 S 32.066 ± 0.006
O 15.9994 ± 0.0003
Multiplicaciones y divisiones :
Cuando se trata de obtener un valor de una medida de forma indirecta,mediante
operaciones diferentes a la suma o a la resta, calcularemos la incertidumbre relativa del
resultado, que corresponde a la raíz cuadrada de la suma de los cuadrados de las
incertidumbres relativas en tanto por uno, seguidamente y a partir de la incertidumbre
encontrada se calcula la incertidumbre absoluta del resultado, aplicando la propia definición
de la incertidumbre relativa
A ± a = (B ± b) * (C ± c)
a / A =
a = A *
Ejemplo de aplicación: Expresa el siguiente resultado con su incertidumbre absoluta

31. [ ( 1,76 + 0,03 ) X ( 1,89 + 0,02 )] / ( 0,554 + 0,008)
Paso 1. Calculamos el resultado prescindiendo de las incertidumbres,
VR= (1,76 X 1,89) / 0,554 = 6,004332...
Paso 2. Determinamos la incertidumbre relativa correspondiente al resultado
IR = (a/A) = = 0,0247194
Paso 3. Determinamos la incertidumbre absoluta del resultado
IR = IA / VR
IA = IR·VR IA = 0,0247194 X 6,004332 = 0,1484...
Paso 4. Expresamos el valor de la incertidumbre absoluta del resultado con dos cifras
significativas ya que la primera es la unidad: IA = 0,15.
Paso 5. Expresamos el resultado
6,00 ± 0,15
Observamos que, si los errores de las medidas experimentales son grandes, también
lo serán en los reultados finales, y en ese caso al resultado le corresponderán menos cifras
significativas.
Todo ello influye en los resultados que por tanto no serán exactos y estarán afectados de
cierta incertidumbre que es preciso determinar en cada caso pues es la que nos indica la
calidad de la medida realizada y debe acompañar siempre al resultado. Así por ejemplo el
resultado de una pesada puede ser:
3,235 + 0,001 g
3,2350 + 0,0001 g
Para la primera el número de cifras decimales garantizadas es dos y para la segunda tres. El
conocimiento del error o incertidumbre, cometido en una medida realizada tiene además
gran importancia para determinar el número de cifras significativas a tomar a la hora de
cálculos posteriores.
La incertidumbre que afecta a las cantidades tomadas de tablas o libros será el de la última
cifra significativa.
Densidad del agua a 18 ºC 0,9987 + 0,0001 g / cc
Tiempo medido con un cronómetro 2,0 + 0,1 s
Tiempo medido con un cronómetro 2,000 + 0,001 s

32. 8. RECAPITULANDO
1.-Todo resultado experimental o medida hecha en el laboratorio debe de ir
acompañada del valor estimado del error de la medida y a continuación, las unidades
empleadas.
Por ejemplo, al medir una cierta distancia hemos obtenido
297±2 mm.
De este modo, entendemos que la medida de dicha magnitud está en alguna parte
entre 295 mm y 299 mm. En realidad, la expresión anterior no significa que se está seguro
de que el valor verdadero esté entre los límites indicados, sino que hay cierta probabilidad de
que esté ahí.
Una medida de 92.81 con un error de 0.3, se expresa
92.8±0.3
Con un error de 3, se expresa
93±3
Ya que al prescindir de la cifra decimal “81”, aumentamos en uno el valor de las
unidades.
Con un error de 30 se expresa
90±30
2.- Los errores se deben dar solamente con una única cifra significativa.
3.-La última cifra significativa en el valor de una magnitud física y en su error,
expresados en las mismas unidades, deben de corresponder al mismo orden de magnitud
(centenas, decenas, unidades, décimas, centésimas).
• Expresiones incorrectas por la regla 2
24567±2928 m
23.463±0.165 cm
345.20±3.10 mm
• Expresiones incorrectas por la regla 3.
24567±3000 cm
43±0.06 m
345.2±3 m
• Expresiones correctas
24000±3000 m
23.5±0.2 cm

33. 345±3 m
43.00±0.06 m
9. EJERCICIOS PROPUESTOS:
1.- Contesta si las siguientes afirmaciones son verdaderas (V) o falsas (F).
a) La longitud, la masa y el tiempo son magnitudes fundamentales.
b) En el Sistema Internacional las longitudes se miden en cm.
c) Los errores accidentales son originados por los aparatos de medida.
d) El error debido al calibrado de un aparato se denomina incertidumbre.
e) El error relativo nos da una visión más fiable de la exactitud de una medida.
2.- Indica cómo deben expresarse cada una de las siguientes medidas:
a) 12.3 g medidos con una balanza que aprecia hasta los dg.
b) 35.6 s medidos con un cronómetro que aprecia hasta las centésimas de segundo.
c) 21.927 m medidos con una regla que aprecia hasta los mm.
3.- ¿Qué medida es más precisa la realizada al determinar la masa de una persona de 60 Kg
con un error de 100 g o la que se obtiene al medir la masa de un coche de 1200 Kg con un
error de 10Kg?
4.- Expresa correctamente las siguientes medidas:
a) 2.273 ± 0.73 m
b) 4.3 ± 0.063 m2
c) 5.943 ± 0.168 cm
d) 223.36 ± 0.37 cm
5.- ¿Con cuantas cifras significativas están expresadas las siguientes cantidades?
a) 0.00852 g
b) 30870 Km
c) 100.74 s
d) 25538.0 m
6.-Escribe cuantas cifras significativas tienen las siguientes cantidades:
2,307 m

34. 0,0025 cm
20,0 Km
10008 Km
0,00003200 m
0,06 cm
7.-Calcula con el número correcto de cifras significativas:
(25,63 * 0,5481 * 0,053000) / 1,1689
50,00 * 27,8 * 0,1167
(42,68 * 891) / (132,6 * 0,5247)
(2,776 * 0,00509 – (6,7 * 10) + (0,0036 * 0,0271)
4,35 + 8,75 + 2,95 + 12,45 + 6,6 + 7,55 + 9,75
48,0 * 943
8,35 / 98
28 * 4193 * 182
(526,7 * 0,001280) / 0,1598
3,145 * (28,7)1/2
10. PRÁCTICAS
PRÁCTICA 1 CALIBRACIÓN DE MATERIAL VOLUMÉTRICO
PRÁCTICA 2 MEDIDA DE LONGITUDES, ESPESORES Y VOLÚMENES
11. BIBLIOGRAFÍA:
ESTADÍSTICA APLICADA AL LABORATORIO. Matilde Azaustre, Joan Sánchez y
Miquel Villalobos. Editorial CEYSA. 2003
FÍSICA J. CATALÁ. FUNDACIÓN GARCÍA MUÑOZ. 1988.
QUIMIOMETRÍA. Guillermo Ramis Ramos, Mª Celia García Alvarez-Coque. Editorial
Síntesis. 2001
GUÍA PARA LA EXPRESIÓN DE LA INCERTIDUMBRE. Centro Español de Metrología.
Ministerio de Fomento. 2000

35. EXPRESIÓN DE LA INCERTIDUMBRE DE LA MEDIDA EN LAS CALIBRACIONES. CEA
ENAC. Enero 98.