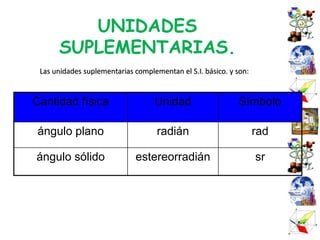
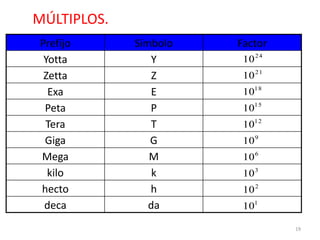
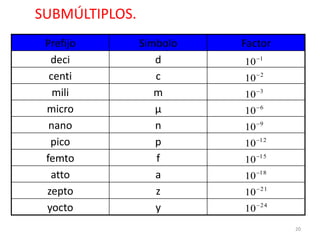
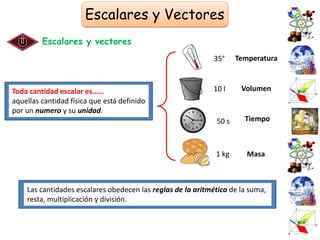
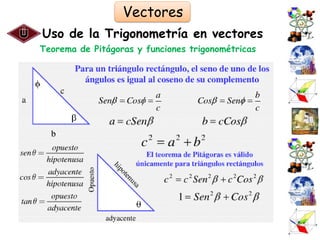
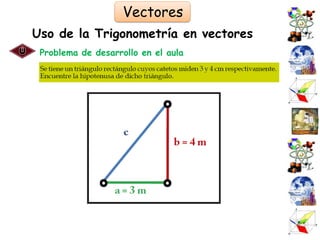
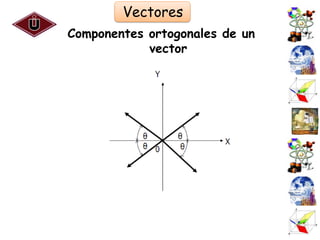
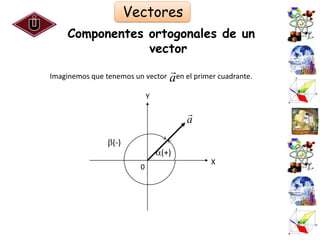
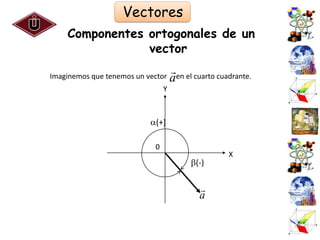
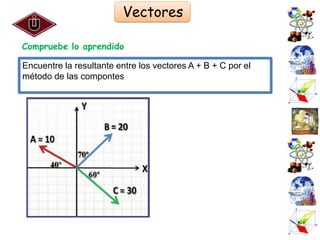
El documento presenta una introducción al Sistema Internacional de Unidades (SI) y conceptos fundamentales como unidades, sistemas de unidades, unidades fundamentales, unidades derivadas y múltiplos/submúltiplos. También explica la diferencia entre cantidades escalares y vectoriales, y cómo representar y calcular componentes de vectores usando trigonometría.

1. FÍSICA
UNIDADES ESTÁNDAR Y
SISTEMAS DE UNIDADES
Expositor:
Marcos Guerrero Zambrano
Marcos Guerrero 1

2. Unidades y Mediciones
Sistemas de
unidades
Todas las mediciones siempre van acompañadas de un número y una unidad.
Si una unidad logra aceptación oficial,
decimos que es una unidad estándar.
Tradicionalmente un organismo gubernamental
o internacional establece las unidades estándar.
Un grupo de unidades estándar y sus
combinaciones se denomina sistema de
unidades.
2

3. SISTEMA INTERNACIONAL S.I.
El Sistema Internacional de Unidades se fundamenta tiene:
Unidades fundamentales.
Unidades suplementarias.
Unidades derivadas.
 Múltiplos y submúltiplos.
UNIDADES FUNDAMENTALES
El Sistema Internacional de Unidades consta de siete unidades básicas,
también denominadas unidades fundamentales. Son las unidades utilizadas
para expresar las cantidades físicas definidas como fundamentales, a partir de
las cuales se definen las demás y son:
3

4. Cantidad física Unidad Símbolo
longitud metro m
tiempo segundo s
masa kilogramo kg
temperatura kelvin K
cantidad de sustancia mol mol
intensidad de corriente ampere A
eléctrica
intensidad luminosa candela cd
Marcos Guerrero 4

5. UNIDADES
SUPLEMENTARIAS.
Las unidades suplementarias complementan el S.I. básico. y son:
Cantidad física Unidad Símbolo
ángulo plano radián rad
ángulo sólido estereorradián sr
5

6. UNIDADES DERIVADAS.
Se llaman así porque están en función de las unidades fundamentales y
suplementarias. Hay un sin número de unidades derivadas sin embargo
mencionaremos las más importantes.
Cantidad física Unidad Símbolo
área metro cuadrado
m2
volumen metro cúbico m3
rapidez lineal y metro por segundo a
m.s 1
velocidad lineal la menos 1
rapidez angular y radián por segundo a rad  s 1
velocidad angular la menos 1
aceleración lineal metro por segundo a la
menos 2 m  s 2
6

7. Cantidad física Unidad Símbolo
aceleración radián por
segundo a la
2
angular menos 2 rad  s
fuerza newton N  kg  m  s 2
trabajo, calor y joule J  N  m  kg.m.s 2 .m  kg  m2  s 2
energía
potencia watt
W  J .s 1  N .m.s 1  kg.m.s 2 .m.s 1  kg.m2 .s 3
7

8. Cantidad física Unidad Símbolo
densidad kilogramo por metro
a la menos 3 kg  m 3
presión pascal
Pa  N .m2  kg.m.s 2 .m2  kg.m1.s 2
torque o newton por
momento metro N  m  kg.m.s 2 .m  kg  m2  s 2
8

9. Cantidad Física: es aquella que va representada con un número que mide y
una unidad de medición
Ejemplo: 20 m
número unidad de
que medición
mide
Es importante indicar que la forma correcta de expresar una unidad, por
ejemplo, aceleración lineal es m.s 2y no m .
s2
9

10. Compruebe lo aprendido
10

11. Compruebe lo aprendido
11

12. Compruebe lo aprendido
12

13. Unidades y Mediciones
Conversión de unidades
Una conversión de unidad simplemente nos permite expresar una cantidad en
términos de otras unidades sin alterar las cantidad física.
Para resolver problemas en los que hay que realizar una conversión de
unidad, debemos tener en cuenta lo siguiente:
1. Para hacer una conversión de unidad(es), debe darse cuenta si es
posible realizar dicha conversión
2. Si es posible hacer la conversión de la(s) unidad(es) debe tener a la
mano el(los) factor(es) de conversión a utilizar en el problema.
3. Utilizar el método escalonado para hacer la conversión de unidad.
13

14. Longitud Tiempo Área Masa
metro (m) segundo (s) metro cuadrado kilogramos (kg)
2
(m )
yarda (yd) minutos (min) acre (acre) tonelada (Tn)
pie (pie) horas (h) pies cuadrados ( gramo (g)
pie 2
)
pulgadas (pulg) año (año) onza (onza)
codo (codo) mes (mes)
millas (mi)
Marcos Guerrero 14

15. Ejercita lo aprendido
m
Convertir 30,8 km a .
h s
Factores de conversión a utilizar:
1km  103 m
1h  3600s

km 103 m 1h
30,8 .
h
x x
1km 3600s
8,5555555555556
m
s
 8,56m.s 1
15

16. Ejercita lo aprendido
Factores de conversión a utilizar:
1kW.h  3,6 x106 J
1eV  1,6 x1019 J
Convertir 300kW.h a eV.
16

17. Ejercita lo aprendido
17

18. Múltiplos y Submúltiplos
Debido a que existen cantidades físicas que tiene una serie de ceros, se utiliza
los múltiplos y submúltiplos del S.I.
Los símbolos de las unidades pueden verse afectados de prefijos que actúan
como múltiplos y submúltiplos.
18

19. MÚLTIPLOS.
Prefijo Símbolo Factor
Yotta Y 10 2 4
Zetta Z 10 2 1
Exa E 101 8
Peta P 101 5
Tera T 101 2
Giga G 10 9
Mega M 10 6
kilo k 10 3
hecto h 10 2
deca da 101
19

20. SUBMÚLTIPLOS.
Prefijo Símbolo Factor
deci d 10 1
centi c 10  2
mili m 10 3
micro μ 10  6
nano n 10 9
pico p 10 12
femto f 10 15
atto a 10 18
zepto z 10  21
yocto y 10  24
20

21. ¿Cómo utilizar los múltiplos y
submúltiplos?
Los múltiplos y submúltiplos se colocan delante del símbolo de la unidad
correspondiente sin espacio intermedio.
Ejemplos:
kilo metro km 103 m
Mega newton MN 106 N
21

22. EJERCICIOS.
Convertir 200MPa a Pa
.
Convertir 300Ts a ms
.
Convertir 5000GW a mW
.
22

23. ESCALARES y VECTORES

24. Escalares y Vectores
Escalares y vectores
Cantidad Física
Una cantidad física es una propiedad o cualidad de
un objeto o sistema físico a la que se le pueden
asignar distintos valores como resultado de una
medición cuantitativa.
Cantidad Escalar Cantidad Vectorial

25. Escalares y Vectores
Escalares y vectores
35° Temperatura
Toda cantidad escalar es…… 10 l Volumen
aquellas cantidad física que está definido
por un numero y su unidad.
50 s Tiempo
1 kg Masa
Las cantidades escalares obedecen las reglas de la aritmética de la suma,
resta, multiplicación y división.

26. Escalares y Vectores
Escalares y vectores
Velocidad
Fuerza
Toda cantidad vectorial es……
aquellas cantidad física que está definido
por magnitud y dirección.
Desplazamiento
Aceleración
Las cantidades vectoriales obedecen reglas distintas conocidas como
algebra vectorial.

27. Vectores
Notación y representación gráfica
de una cantidad vectorial
 La magnitud está dada por la
longitud del vector “flecha”.
 La dirección viene dado por
el ángulo (medido con respecto a un eje)
y la flecha
Punto de aplicación donde nace el vector
A
Dirección
θ
X

28. Vectores
Notación y representación gráfica
de una cantidad vectorial
Un vector se lo denota con las letras mayúsculas o minúsculas, con una
flecha en la parte superior o con negrillas.
A A
=
La magnitud de un vector se lo denota entre barras.
|A|= A

29. Vectores
Compruebe lo aprendido
¿Cuál de los siguientes vectores tiene magnitud negativa?
No existe
magnitud
negativa
a) b) c) d) e)

30. Vectores
Compruebe lo aprendido
Indique, ¿cuál de las siguientes alternatrivas es una cantidad
vectorial?
A. Masa
B. Temperatura
C. Aceleración
D. Tiempo
E. Pienso que mas de uno es una cantidad vectorial

31. Vectores
Uso de la Trigonometría en vectores
Teorema de Pitágoras y funciones trigonométricas

32. Vectores
Uso de la Trigonometría en vectores
Problema de desarrollo en el aula

33. Vectores
Uso de la Trigonometría en vectores
Problema de desarrollo en el aula
En la figura se muestra un auto escalera que se encuentra a 1,8m
de la pared y la escalera que es manejada por el auto tiene 3,5 m
de longitud. ¿Cuál será la altura de la pared?

34. Vectores
Uso de la Trigonometría en vectores
Problema de desarrollo en el aula

35. Vectores
Uso de la Trigonometría en vectores
Problema de desarrollo en el aula

36. Vectores
El vector Opuesto
El vector OPUESTO a un vector V se presenta por –V; tiene el mismo
módulo pero su dirección es contraria (Se rota el vector original 180º)
V
180º
-A A
-V

37. Vectores
Compruebe lo aprendido

38. Vectores
Componentes ortogonales de un
vector

39. Vectores
Componentes ortogonales de un
vector
Imaginemos que tenemos un vector en el primer cuadrante.
Y
 Del gráfico podemos observar
 a que:
ay
  
a  ax  a y
 X
0 ax  

a x y a y son llamados componentes
ortogonales del vector a o proyecciones

del vector a a lo largo de los ejes x e y
respectivamente.

40. Vectores
Componentes ortogonales de un
vector
en el segundo cuadrante.
Imaginemos que tenemos un vector a
Y

a

ay
0 X
ax
40

41. Vectores
Componentes ortogonales de un
vector
Imaginemos que tenemos un vector r en el tercer cuadrante.
a
Y

ax 0
 X
ay

a
41

42. Vectores
Componentes ortogonales de un
vector
en el cuarto cuadrante.
Imaginemos que tenemos un vector a
Y

0 ax
 X
ay

a
42

43. Vectores
Componentes ortogonales de un
vector

Imaginemos que tenemos un vector a en el eje x(+).
Y
 
0 a  ax
X


Como el vector ase encuentra en el eje x la componente del vector
 
en el eje yaes .
ay  0
43

44. Vectores
Componentes ortogonales de un
vector

Imaginemos que tenemos un vector aen el eje y(-).
Y
0
X
 
a  ay


Como el vector a se encuentra en el  y la componente del vector
 eje
en el eje xa es .
ax  0
44

45. Vectores
Componentes ortogonales de un
vector
Para determinar las magnitudes de las componentes de un vector a lo largo de los
ejes x e y respectivamente, se necesita la magnitud del vector y el ángulo que
forma el vector con el eje horizontal o vertical.

Imaginemos que tenemos el ángulo θ y la magnitud del vector a
Y Utilizando las funciones
trigonométricas Coseno y Seno

 a para el ángulo θ tenemos:
ay ax
Cos   ax  aCos
 a
 X ay
Sen   a y  aSen
0 ax
a
45

46. Vectores
Componentes ortogonales de un
vector

Ahora imaginemos que tenemos el ángulo  y la magnitud del vector
a
Y
Utilizando las funciones
 trigonométricas Coseno y Seno
 a para el ángulo  tenemos:
ay ay
 Cos 
a
 a y  aCos
ax
0
 X Sen   ax  aSen
ax a
46

47. Vectores
Componentes ortogonales de un
vector
SIGNO DE LAS COMPONENTES DE
UN VECTOR. Y

Cuadrante II 
Cuadrante I
ax  () ax  ()
 
a y  () a y  ()
X
0

Cuadrante III 
Cuadrante IV
ax  () ax  ()
 
a y  () a y  ()
47

48. Vectores
Componentes ortogonales de un
vector
MAGNITUD DE UN VECTOR.
  
Imaginemos que conocemos las componentes a xy a y del vector a
.
Y
Podemos utilizar el teorema de
 
Pitágoras para determinar la
 a a
magnitud del vector , entonces
a y
tenemos:
 X
a  ax  a y
2 2
0 ax
48

49. Vectores
Componentes ortogonales de un
vector
DIRECCIÓN DE UN VECTOR.
La dirección de un vector se lo mide con respecto al eje x(+). Si la dirección se la
mide a favor del movimiento de las manecillas del reloj el ángulo es negativo,
pero si la dirección se la mide en contra del movimiento de las manecillas del
reloj el ángulo es positivo.
49

50. Vectores
Componentes ortogonales de un
vector
 
Para determinar la dirección de un vector, imaginemos que conocemos las

componentes a
x
ya y del vectora .
Y Utilizando la siguiente función
trigonométrica tenemos:

 a
ay
ay
Tan 
θ ax
0
 X
ax
Cada vez que se utilice esta ecuación debemos
tener presente que el ángulo θ es el que
forma el vector con el eje horizontal.
50

51. Vectores
Componentes ortogonales de un
vector
51

52. Vectores
Componentes ortogonales de un
vector
en el primer cuadrante.
Imaginemos que tenemos un vector a
Y

a
(-)
(+)
X
0
52

53. Vectores
Componentes ortogonales de un
vector
en el segundo cuadrante.
Imaginemos que tenemos un vector a
Y

a
(+)
X
0
(-)
53

54. Vectores
Componentes ortogonales de un
vector
en el tercer cuadrante.
Imaginemos que tenemos un vector a
Y
(+)
0
X
(-)

a
54

55. Vectores
Componentes ortogonales de un
vector
en el cuarto cuadrante.
Imaginemos que tenemos un vector a
Y
(+)
0
X
(-)

a
55

56. Vectores
Suma de vectores por
Componentes ortogonales
Se lo puede utilizar cuando se tiene 2 o más vectores.
Se lo puede utilizar en la operación de suma y resta entre vectores.
El método consiste en:
•Colocar los vectores de tal manera que sus puntos de aplicación coincidan con
el origen de coordenadas.
•Dibujar las componentes de cada vector, trazando paralelas a los ejes X y Y
respectivamente
•Determinar las magnitudes de las componentes de cada vector utilizando las
funciones trigonométricas básicas seno y coseno.
•Colocar el signo de las componentes de cada vector según el cuadrante
respectivo en el que se encuentre el mismo.
56

57. Vectores
Suma de vectores por
Componentes ortogonales
•Determinar las componentes del vector resultante.
•Dibujar el vector resultante en el cuadrante respectivo.
•Determinar la magnitud del vector resultante con ayuda del teorema de
Pitágoras.
•Determinar la dirección del vector resultante, para esto se puede utilizar la
función trigonométrica como herramienta adicional.
57

58. Vectores
Compruebe lo aprendido
58

59. Vectores
Compruebe lo aprendido
Dos vectores A y B se muestran a continuación. Considere el
vector C = A+B. ¿Cuál es la componente del vector C en y?
(cada lado del cuadrado vale 1 u)
y
x
A) 3
B) 2 A
C) -2
B
D) -4
E) Ninguno de ellos es la respuesta.
59

60. Vectores
Compruebe lo aprendido
Encuentre la resultante entre los vectores A + B + C por el
método de las compontes
60