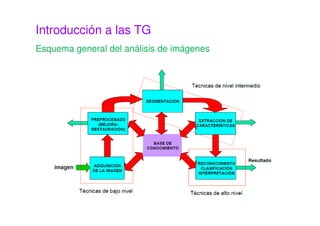
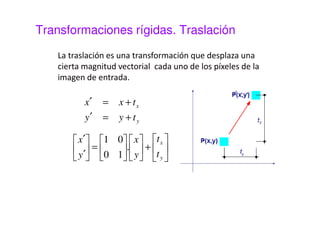
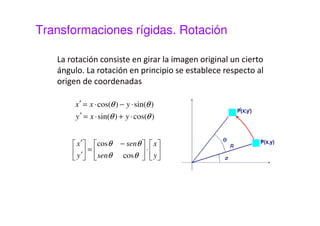
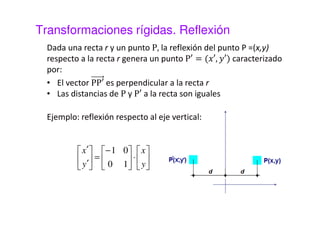
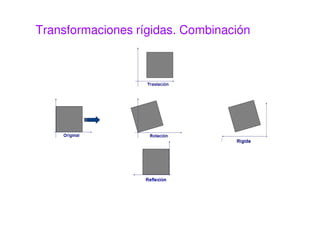
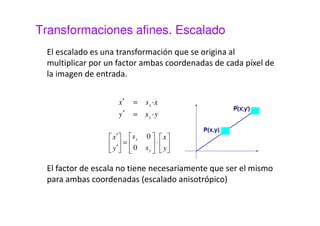
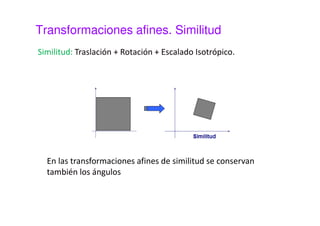
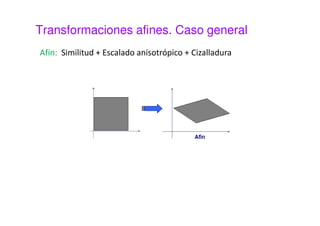
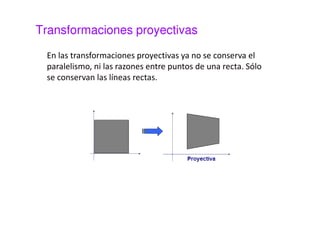
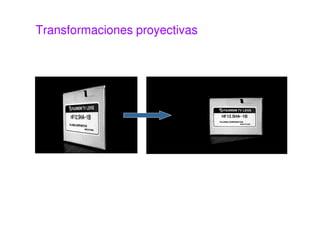
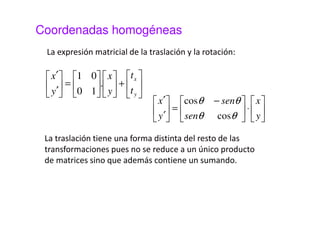
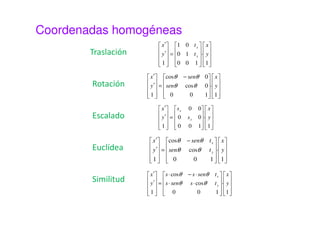
Este documento presenta una sesión sobre transformaciones geométricas de imágenes digitales. Explica los diferentes tipos de transformaciones como rígidas, afines y proyectivas, detallando operaciones como traslación, rotación, escalado y cizalladura. También introduce el uso de coordenadas homogéneas para representar las transformaciones de forma uniforme mediante matrices. Finalmente, muestra cómo aplicar transformaciones geométricas y combinarlas usando MATLAB.

1. Procesamiento de Imágenes
y Visión Artificial
(WEE2)
Sesión: 8
Transformaciones geométricas
MSc. Ing. José C. Benítez P.

2. Logros de aprendizaje
1. Conocer las transformaciones geométricas aplicadas a los
diferentes tipos de imágenes digitales.
2. Transformar geométricamente las imágenes digitales.
3. Implementar funciones para las transformaciones
geométricas de las imágenes digitales.
4. Aplicar transformaciones rígidas sobre una imagen digital.
5. Transformar por afinidad una imagen digital.
6. Conocer las coordenadas homogéneas.
7. Combinar transformaciones geométricas.
2

3. 3
Contenido
Transformaciones geométricas:
• Introducción
• Transformaciones Rígidas
Traslación
Rotación
Reflexión
• Transformaciones Afines
Escalado
Cizalladura
Similitud
• Transformaciones Proyectivas
Coordenadas Homogéneas
• Combinación de Transformaciones
• Transformaciones geométricas con MATLAB

4. Introducción a las TG
Esquema general del análisis de imágenes

5. Introducción a las TG
• Utilizando el histograma, se obtiene una transformación que
asigna para cada nivel de gris de la imagen de entrada un
nuevo nivel de gris. Este tipo de transformaciones se llaman
puntuales pues sólo hace falta conocer el nivel de gris en
cada punto de la imagen de entrada para obtener el valor en
el mismo punto de la imagen de salida.
• Ahora nos ocuparemos de las TG. Determinaremos qué
posición tomará en la imagen destino cada píxel de la imagen
original cuando sobre ella aplicamos una transformación
geométrica tales como traslación, rotación, escalado... Es
decir, el valor de un píxel en la imagen de salida se asignará
en base a las coordenadas (x,y) de ese píxel.

6. Introducción a las TG
• Las TG que veremos no son distintas de las
transformaciones básicas de la geometría. Sin
embargo, debido a la naturaleza discreta de las
imágenes, aparecen ciertos problemas que es preciso
analizar y resolver.
• Este tipo de transformaciones resultan útiles para
facilitar el reconocimiento de formas cuando no
existen unas condiciones preestablecidas de escala o
posición en las piezas a analizar.

7. Introducción a las TG
• Las transformaciones geométricas también son utilizadas para
eliminar distorsiones debidas a óptica y a la perspectiva o
bien para reajustar imágenes de una misma escena tomadas
bajo distintas condiciones y poder de esta forma establecer
correspondencias entre unas y otras.

8. Introducción a las TG
Podemos clasificar las TG en:
• Transformaciones rígidas o euclídeas, que
preservan las distancias, ángulos y áreas.
• Transformaciones afines, que preservan la
colinealidad de los puntos, paralelismos y las
razones entre los puntos pertenecientes a una
línea.
• Transformaciones proyectivas, que preservan
solo la colinealidad de los puntos.

9. Introducción a las TG
En transformaciones rígidas y afines las coordenadas de la
imagen de salida (x¢, y¢)
se obtienen a partir de la ecuación
lineal en las coordenadas de la imagen
=
+

10. =
+
M debe cumplir la condición de ser invertible.

11. Transformaciones rígidas
Las transformaciones rígidas se caracterizan
por preservar las distancias. M es una matriz
ortogonal. Son transformaciones rígidas :
Traslación
Rotación
Reflexión

12. Transformaciones rígidas. Traslación
La traslación es una transformación que desplaza una
cierta magnitud vectorial cada uno de los píxeles de la
imagen de entrada.
x
y
¢ = +
x x t
¢ = +
y y t
x
t
+
1 0
=
¢
¢
y
t
x
y
x
y
.
0 1

13. Transformaciones rígidas. Rotación
La rotación consiste en girar la imagen original un cierto
ángulo. La rotación en principio se establece respecto al
origen de coordenadas
¢ = × − ×
q q
cos( ) sin( )
x x y
¢ = × + ×
q q
sin( ) cos( )
y x y
×
−
=
¢
¢
x
y
q q
sen
sen
x
y
q q
cos
cos

14. Transformaciones rígidas. Reflexión
Dada una recta r y un punto P,la reflexión del punto P =(x,y)
respecto a la recta r genera un punto P′ = (′, ′) caracterizado
por:
• El vector PP′ es perpendicular a la recta r
• Las distancias de P y P′ a la recta son iguales
Ejemplo: reflexión respecto al eje vertical:
×
−
=
¢
¢
x
y
x
y
1 0
0 1

15. Transformaciones rígidas. Combinación

16. Transformaciones afines.
Las transformaciones afines preservan la colinealidad
de los puntos (las rectas siguen siendo rectas tras la
transformación), el paralelismo y las razones entre los
puntos de pertenecientes a una recta.
=
M es una matriz invertible.
+

17. =
+

18. Transformaciones afines.
Las transformaciones afines incluyen:
Escalado
Cizalladura
Similitud

19. Transformaciones afines. Escalado
El escalado es una transformación que se origina al
multiplicar por un factor ambas coordenadas de cada píxel de
la imagen de entrada.
¢ =
x s x
x
·
y s y
y
·
¢ =
×
=
¢
¢
x
y
s
s
x
y
y
x
0
0
El factor de escala no tiene necesariamente que ser el mismo
para ambas coordenadas (escalado anisotrópico)

20. Transformaciones afines. Cizalladura
La cizalladura de x respecto a y desplaza cada píxel de la
imagen original en la dirección x un espacio proporcional a
su coordenada y.
¢ = + ×
x x c y x
¢ =
y y
×
1
x x
c x
=
¢
¢
y
y
0 1

21. Transformaciones afines. Similitud
Similitud: Traslación + Rotación + Escalado Isotrópico.
En las transformaciones afines de similitud se conservan
también los ángulos

22. Transformaciones afines. Caso general
Afín: Similitud + Escalado anisotrópico + Cizalladura

23. Transformaciones proyectivas
En las transformaciones proyectivas ya no se conserva el
paralelismo, ni las razones entre puntos de una recta. Sólo
se conservan las líneas rectas.

24. Transformaciones proyectivas

25. Transformaciones proyectivas

26. Coordenadas homogéneas
La expresión matricial de la traslación y la rotación:
x
t
+
=
¢
¢
y
t
x
y
x
y
.
1 0
0 1
×
−
¢
x
q q
La traslación tiene una forma distinta del resto de las
transformaciones pues no se reduce a un único producto
de matrices sino que además contiene un sumando.
=
¢
x
y
sen
sen
y
q q
cos
cos

27. Coordenadas homogéneas
• Interesa que todas las transformaciones tengan una
representación uniforme mediante un producto de
matrices. Esto permitirá operar más eficientemente,
especialmente cuando hay que realizar una secuencia
de transformaciones.
• Para lograr esta representación matricial uniforme
recurriremos a la utilización de coordenadas
homogéneas.
• En coordenadas homogéneas los puntos del plano se
representan con tres coordenadas.

28. Coordenadas homogéneas
Un punto (x, y) tiene la forma (hx, hy, h), donde h toma un
valor arbitrario distinto de 0 que representa un factor de
escala.
Un mismo punto tiene infinitas representaciones en
coordenadas homogéneas. El punto (2, 3) puede
expresarse como:
(2, 3, 1), (4,6,2), (6, 9, 3), …
No obstante, lo habitual es tomar h=1, con lo que el punto
(x, y) pasa a ser (x, y, 1)

29. Coordenadas homogéneas
La traslación se expresará entonces en coordenadas
homogéneas de la forma:
x
¢
x
=
¢
¢
x
1
·
1 0
0 1
t
x
m m t
11 12
21 22
x
x
1 0 0 1
y
m m t
y
y
=
¢
1
·
0 0 1
1
y
t
y
y
Y en general cualquier transformación afín como:

30. Coordenadas homogéneas
1 0
=
¢
¢
x
1
·
0 1
t
x
0 0 1
x
1
y
t
y
y
−
=
¢
¢
x
1
·
q q
cos 0
cos 0
0 0 1
x
1
y
sen
sen
y
q q
=
¢
¢
x
1
·
0 0
0 0
0 0 1
x
1
y
s
s
y
y
x
−
=
¢
¢
x
1
·
q q
sen t
cos
cos
x
0 0 1
x
1
y
sen t
y
y
q q
Traslación
Rotación
Escalado
Euclídea
q q
× − ×
cos
s s sen t
× ×
=
¢
¢
x
1
·
cos
x
0 0 1
x
1
y
s sen s t
y
y
q q
Similitud

31. Combinación de transformaciones
Cuando se aplican dos o más transformaciones de forma
consecutiva, estas se pueden combinar en una única
transformación sin más que multiplicar las matrices de
transformación. Esta es otra de las grandes ventajas de
trabajar con coordenadas homogéneas.
Ejemplo dos traslaciones:
=
0 0
0 0

32. 0 0 1
0 0
0 0

33. 0 0 1
=
0 0
+
0 0

34. +